Algoritmos 101

Cursos Python

Categoría: 1ra Evaluación

  • 1Eva_IT2014_T2 Verificar EAN con Python

    1ra Evaluación I Término 2014-2015. Julio 1, 2014 /ICM00794

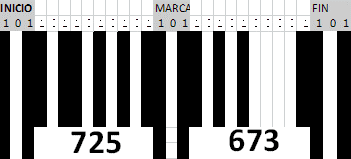
    Tema 2. (25 puntos) El número EAN-13 (European Article Number) usado comercialmente en Europa en la identificación de productos, está constituido por 13 dígitos y con una estructura dividida en cuatro partes :

    • 3 dígitos para el país,
    • 4 dígitos para la empresa,
    • 5 dígitos para el producto, y
    • un dígito de control.

    El dígito de control permite detectar errores de lectura del código, calculado como:

    • Comenzando por la derecha, se multiplican los dígitos del código por 1 si su posición es par y por 3 si es impar,
    • Se suman los valores de los productos obtenidos,
    • Se resta a la decena superior el resultado de la suma, siendo el resultado el dígito de control.
    7 7 0 2 0 0 4 0 0 3 5 0
    x1 x3 x1 x3 x1 x3 x1 x3 x1 x3 x1 x3
    7 21 0 6 0 0 4 0 0 9 5 0 
    Suma = 52
 decena superior = 60
 verificador calculado 60-52 = 8

    Realice un algoritmo que dado un número EAN valide que sea de 13 dígitos, calcule el dígito verificador e informe si es correcto.

    Referencia: http://es.wikipedia.org/wiki/European_Article_Number

    Rúbrica: Ingreso y validación (5 puntos), cálculos por dígito (10 puntos), decena superior (5 puntos), resultado (5 puntos)

  • 1Eva_IIT2014_T4 Turnos en imprenta de gigantografía

    1ra Evaluación II Término 2014-2015. Diciembre 9, 2014 /ICM00794

    Tema 4. (30 puntos). Una empresa de gigantografías registra los pedidos de trabajo por cliente como la cantidad de letreros a imprimir y los atiende por orden de llegada. 

    Cada operador de la imprenta trabaja en turnos de 4 horas (240 minutos), y le toma 25 minutos imprimir un letrero en la máquina.

    Al terminar el turno de trabajo (4 horas), el operador debe informar al siguiente:

    a) el número de clientes con pedidos completados,

    b) el cliente cuyo pedido se está trabajando.

    c) La cantidad de letreros completados del pedido que se está atendiendo.

    Realice un algoritmo que permita ingresar en un arreglo la cantidad de pedidos por cliente (pedido [cliente]) y pueda estimar las respuestas del informe para el cambio de turno.

    Ejemplo:

    cliente 1 2 3 4 5 6 7
    pedido [cliente] 3 2 1 2 2 4 1
    tiempo [cliente] 75 50 25 50 50 100 25
    total tiempo [cliente] 75 125 150 200 250 350 375
    turno de operador 1 1 1 1 2 2 2 
    Al cambio de turno:
 pedidos completados: 4
 Atendiendo a cliente: 5
 Letreros completados del pedido: 1

    En el ejemplo, se encuentra que:

    • los pedidos completados por el operador  1 fueron solo 4, pues el 5 todavía se está trabajando,
    • los letreros completados del pedido del cliente 5 son 1. (calculado como el cociente (240-200)/25)).

    Rúbrica: Ingreso (5 puntos), conversión a tiempos (5 puntos), literal a) (5 puntos), literal b) (5 puntos), literal c) (10 puntos)

  • 1Eva_IIT2014_T3 Parasailing sin sobrecarga, parejas

    1ra Evaluación II Término 2014-2015. Diciembre 9, 2014 /ICM00794

    Tema 3. (25 puntos) Parasailing es un tipo de deporte extremo de playa promocionado para turistas que usa un paracaídas para dos personas atado e impulsado por una lancha. parasailing dibujo

    Por seguridad, la capacidad del paracaídas máxima es de 350 lb.

    Dada la capacidad máxima y la lista de los pesos en libras para n turistas en la cola, realice un algoritmo para determinar las combinaciones posibles de parejas entre las personas en la cola de espera sin sobrecargar el paracaídas.

    Ejemplo: capacidad máxima=350; Cola de espera:

    i 1 2 3 ...
    pesos[i] 120 180 165 ...

    Referencia: publicado el 21-feb-2012. https://www.eltelegrafo.com.ec/noticias/deportes/1/el-parasailing-los-hace-sentirse-duenos-del-cielo

    Rúbrica: ingreso de datos (5 puntos), seleccionar y comparar parejas (15 puntos), conteo de pareja (5 puntos)

  • 1Eva_IIT2014_T2 Triángulos aleatorios en rectángulo

    1ra Evaluación II Término 2014-2015. Diciembre 9, 2014 /ICM00794

    Tema 2. (25 puntos) Una imagen para protector de pantalla en computadora se puede generar dibujando triángulos de tamaño y posición aleatorias.

    triangulos01

    Para formar un triángulo se generan tres pares ordenados dentro de un rectángulo de lados a y b.

    Elabore un algoritmo que genere aleatoriamente los vértices para n triángulos y determine la cantidad de figuras generadas clasificadas como:

    • triángulos equiláteros, todos sus lados de iguales
    • triángulos escalenos, todos sus lados diferentes
    • triángulos isósceles, dos lados iguales y uno desigual
    • puntos colineales, la suma de dos lados es igual al tercer lado y NO forma un triángulo.
    Ejemplo:
>>> ¿cuántos triángulos?: 5
 ¿lado a?: 10
 ¿lado b?: 10
 equiláteros: 0
 escaleno: 3
 isósceles: 1
 colineales: 1

    Rúbrica: Ingreso y validación (5 puntos), triángulos aleatorios en el plano (5 puntos), contar por tipo (10 puntos), contar colineales (5 puntos)

  • 1Eva_IT2013_T4 Tabular atención al cliente

    1ra Evaluación I Término 2013-2014, Julio 2, 2013 /ICM00794

    Tema 4. (30 puntos) En un "Centro de Servicio",  el cliente luego de ser atendido evalúa la atención recibida presionando un botón entre las 5 opciones mostradas. 

    Opciones:
 5. Excelente
 4. Muy Buena
 3. Buena
 2. Regular
 1. No satisfactoria

    Realice un algoritmo que registre en un arreglo la evaluación para n clientes atendidos, luego deberá tabular las respuestas para mostrar:

    a) Total de respuestas por tipo
    b) La respuesta más frecuente
    c) ¿Cuáles clientes respondieron con valores menores al promedio?

    Ejemplo: n=50
    Cliente  1  2 3  4 5  ... n
    Atención  5  2 4  5  3  ...  4 
    Respuestas
a) Excelente: 10
 Muy Buena: 20
 Buena: 15
 Regular: 3
 No satisfactoria: 2
b) Más frecuente: 4
c) Promedio: 3.66
menor al prom.:
2,5,…etc

    Rúbrica: Ingreso y validación (5 puntos),  literal a (10 puntos) literal b (10 puntos). Algoritmo estructurado (5 puntos)

  • 1Eva_IIT2013_T4 Sorteo series mundial de fútbol

    1ra Evaluación II Término 2013-2014. Diciembre 3, 2013 /ICM00794

    Tema 4. (30 puntos) Una vez conocidas las 32 selecciones que participarán del próximo mundial de fútbol se necesita realizar el sorteo entre las 8 series o grupos de competencia.

    Las selecciones se encuentran numeradas del 1 al 32, las mejores han sido pre asignadas como “cabeza de serie”; una por cada grupo y no se sorteará su ubicación en la serie.

    Las selecciones restantes se sortearán la ubicación en cada serie (grupo) para completar los cuatro participantes por serie.

    grupo 1 2 3 4 5 6 7 8
    cabeza [grupo] 3 7 9 12 22 25 26 30

    El sorteo de serie (luego de copiar los cabezas de grupo) ser realizará en un vector como el mostrado:

    selección 1 2 3 4 5 6 7 8 9 ... 32
    serie [selección] 0 0 1 0 0 0 2 0 3 ... 0

    Elabore un algoritmo que solicite cuáles son los 8 equipos que serán cabezas de serie, asigne aleatoriamente (y sin repeticiones) los 24 equipos restantes, al final muestre el listado de las series resultantes.

    Rúbrica: Ingreso (5 puntos), definir pre-asignados (5 puntos), sorteos no repetidos (15 puntos), presentación de resultados (5 puntos).

  • 1Eva_IT2013_T3 Generar tarjetas pre pago

    1ra Evaluación I Término 2013-2014, Julio 2, 2013 /ICM00794

    Tema 3. (20 puntos) Una tarjeta prepago que se activa y valida por llamada telefónica o internet utiliza dos números: tarjeta prepago dibujo

    • la serie y
    • una clave

    ambos números hacen única a la tarjeta y se usan como método de registro y seguridad.

    La serie  se compone de 8 dígitos que corresponden a la identificación de la tarjeta dentro de un rango de producción, la clave es un número de 6 dígitos generados de forma aleatoria [100000, 999999];

    Elabore un algoritmo que permita
    a) generar n tarjetas prepago dentro de un rango de serie con su correspondiente clave de validación.
    b) Muestre cuántas tarjetas tienen claves impares y cuántas pares.
    c) Muestre la tabla de las series y sus claves

    Ejemplo:
    ¿Cuántas tarjetas?: 1000
    ¿Serie Inicial?:  2531 1001    		 Tarjeta Serie Clave
    1 2531 1001 725 673
    2 2531 1002 428 095
    ... ... ...
    1000 2531 2000 152 652

    Rúbrica: Ingreso (5 puntos), literal b (10 puntos), literal c (5 puntos).

     

  • 1Eva_IIT2013_T3 Juego Semillero

    1ra Evaluación II Término 2013-2014. Diciembre 3, 2013 /ICM00794

    Tema 3. (30 puntos) Semillero es un juego con n jugadores que buscan obtener al final más fichas de las que aportan para jugar. semillero juego fichas

    Todos los jugadores participan con m fichas, depositándolas en un recipiente común en el juego.enteros aleatorios dados

    En cada turno, el jugador lanzará dos dados y obtendrá fichas del recipiente común equivalente a la suma de las caras superiores de los dados.

    El juego termina cuando no quedan más fichas en el recipiente, mostrando: el jugador con más fichas, el jugador que vació el recipiente y las fichas obtenidas por jugador.

    Realice un algoritmo que simule el juego descrito, considerando lo siguiente:

    • El número de fichas por participante m es igual para todos los participantes, mínimo 20 (validar)
    • Los turnos son rotativos: jugador 1, jugador 2, …, jugador n, jugador 1,  jugador 2, …, jugador n, …
    • El juego finaliza en cualquier turno, cuando se acaban las fichas.
    • Al final se extraen solo las fichas restantes en el recipiente, pues el total de fichas restantes solo puede llegar a 0.
    • Para encontrar al ganador, debe describir el algoritmo, NO use funciones de matlab.

    Rúbrica: Ingreso y validación (5 puntos), control de turnos (5 puntos). Control de fichas (10 puntos). Busca ganador (5 puntos), resultados (5 puntos).

  • 1Eva_IIT2013_T2 Números palíndromo con Python

    1ra Evaluación II Término 2013-2014. Diciembre 3, 2013 /ICM00794

    Tema 2. (25 puntos)

    Un número palíndromo es un número que se lee igual de izquierda a derecha que de derecha a izquierda.

    Realice un algoritmo que permita:

    Ejemplo:
 Números palíndromo: 2002, 1991, 2112.
 No son números palíndromo: 2013, 1492

    a) Invertir los dígitos de un número y verificar si el número es palíndromo

    b) Buscar los números palíndromo con más de dos cifras y que sean menores a 1 millón.

    Rúbrica: literal a (10 puntos), literal b, manejo de rangos (5 puntos) y respuesta (5 puntos). Algoritmo integrado (5 puntos)

  • 1Eva_IT2013_T2 Código de barras- simbología discreta

    1ra Evaluación I Término 2013-2014, Julio 2, 2013 /ICM00794

    Tema 2. (25 puntos) El código de barras utiliza líneas paralelas verticales (barras y espacios) que representan información en su equivalente binario.

    El código es muy usado en los puntos de ventas y es “leído” por un dispositivo láser (scanner).

    Para facilitar la lectura por scanner se usa el método de “simbología discreta”, en el que se marca el inicio, separación y fin de los datos con  la secuencia barra/espacio/ barra (101) por cada grupo de 10 bits (dígitos binarios).

    Elabore un algoritmo que permita cambiar un código de producto conformado por dos números de 3 cifras a su equivalente en código de barras usando simbología discreta.

    >> codigobarras
1er Número: 725
2do Número: 673
101 1011010101 101 1010100001 101

    Nota Matlab: Mostrar todos los dígitos fprintf('% .0d ', número).
    Referencia: http://es.wikipedia.org/wiki/C%C3%B3digo_de_barras
    Rúbrica: Cambio decimal a binario (10 puntos), simbología discreta (10 puntos), resultado (5 puntos).

    Referencia: Cadenas de Supermercados - Gigantes de la comida. History Latinoamérica. 18 Julio 2025. minuto 8:15 códigos de barra.