Algoritmos 101

Cursos Python

Categoría: Evaluaciones

Ejercicios de examen

  • 1Eva_IT2005_T4 Lanza penales

    Parcial I Término 2005 - 2006. Julio 05, 2005 /ICM00794

    Tema 4. (30 puntos) En el Fútbol el lanzamiento de penales intervienen el jugador que patea y el arquero que tapa el penal.

    Este juego consiste en 5 lanzamientos por parte de los jugadores que patean el balón, los cuales pueden decidir lanzar en cualquiera de las seis secciones del arco (1: arriba a la derecha, 2: arriba al centro, 3: arriba a la izquierda, 4 abajo a la izquierda, 5: abajo al centro, 6: abajo a la derecha).

    En cada lanzamiento, el arquero decide donde ubicarse para atajar el tiro y no tiene oportunidad de cubrir otra sección, si éste coincide con la ubicación donde disparó el jugador, entonces el lanzamiento fue atajado o fallado, caso contrario se marcó un GOL.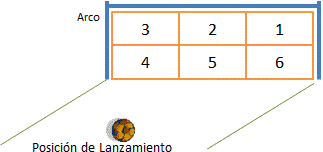

    Escriba un algoritmo que simule un juego de 5 lanzamientos de penales, en donde la sección del arco donde cada jugador lanza es decidido por el usuario y la sección cubierta por el arquero es simulado por el computador (aleatoria).

    Al final presente la siguiente información:

    a) Cantidad de goles conseguidos.

    b) Cantidad de penales fallados.

    c) La cantidad de goles realizados en la parte derecha, central e izquierda del arco.

    d) La ubicación del arco (derecha, centro o izquierda) por donde ingresaron más goles. Suponga que existe una sola.

    e) La ubicación del arco (derecha, centro o izquierda) por donde no ingresaron goles. Suponga que existe una sola.

    Rúbrica: literal a (5 puntos), literal b (5 puntos), literal c (5 puntos), literal d (5 puntos), literal e (5 puntos), estructuras completas (5 puntos), contadores y acumuladores inicializados y en orden (5 puntos).

  • 1Eva_IT2005_T3 Arreglo aleatorio binario a decimal

    Parcial I Término 2005 - 2006. Julio 05, 2005 /ICM00794

    Tema 3. (30 puntos). Suponga un vector B[i] de n componentes enteros.1Eva_IT2005_T3 binario a Decimal

    Diseñe un algoritmo estructurado que almacene en cada celda un número aleatorio binario de una cifra (1 ó 0).

    a) Determine si la cantidad de 1’s es par o impar
    b) Calcule el equivalente numérico decimal del número binario almacenado.
    c) Muestre los resultados de los literales a) y b).

    Ejemplo: Vector B[i] con n=8, equivalente a un binario B=11010010

    i B[i] Equivalente decimal:
    1 1 1*27+
    2 1 1*26+
    3 0 0*25+
    4 1 1*24+
    5 0 0*23+
    6 0 0*22+
    7 1 1*21+
    8 0 0*20
    Total de 1’s es Par =21010

    Rúbrica: ingreso de tamaño de vector (3 puntos), ingreso de datos del vector, o generar aleatorios (7 puntos), literal a (5 puntos), literal b (10 puntos), literal c (5 puntos)

  • 1Eva_IIT2005_T3 Entrenamiento atleta: promedios

    Parcial II Término 2005 - 2006. Diciembre 06, 2005 /ICM00794

    Tema 3. (30 puntos). Un atleta se ha propuesto recorrer una misma ruta durante un año, corriendo 7 días a la semana, para así saber su promedio de tiempo por cada semana, por cada mes y por todo el año.

    Suponga que todos los meses son de 30 días.

    Los datos que se proporcionan son 360 valores reales en minutos, que indican el tiempo del recorrido registrado para cada día.

    Elabore el algoritmo que proporcione al atleta la información que desea conocer.

    día tiempo semana mes
    1 40.5 39.8
    2 39.8
    3 41.3
    4 38.8
    5 40.1
    6 39.4
    7 41.2  40.15
    8 41.1
    9 40.9
    10 39.8
    11 42.1
    12 40.3
    13 38.7
    14 38.4  40.18
    15 ... ...
    ... ...  Bloque de
    30 dias

    Nota: Para desarrollar el ejercicio en computador, genere los 360 valores de forma aleatoria, así podrá probar el algoritmo.

    Se obtiene por ejemplo un vector para promedio por mes:

    mes  1 2 3 4 5 6 7 8 9 10 11 12
    PromedioM[mes]  39.8  ...  ...

    y de forma semejante el promedio por semana.

  • 1Eva_IIT2005_T2 Negocio piramidal

    Parcial II Término 2005 - 2006. Diciembre 06, 2005 /ICM00794

    Tema 2. (25 puntos). negociopiramide

    Considere el desarrollo del siguiente negocio:

    a. Una persona entrega x dólares, y se le paga 10% mensual del valor inicial depositado en forma permanente.

    b. Suponga que las personas NO retiran el dinero depositado, solo los intereses que se generan

    c. La persona que recibe el dinero de los participantes usa el 20% del dinero x depositado de cada persona como comisión por gestión y gastos, quedando como saldo lo que había menos intereses y menos comisiones.

    d. Suponga que cada mes se duplica la cantidad de personas que invierte la misma cantidad x de dinero, con las mismas condiciones.

    e. Pero únicamente hay n personas que pueden entrar al negocio.

    Describa un algoritmo para determinar en cuál mes no habrá suficiente dinero para pagar a los depositantes.

    Referencia: Estafas piramidales son repetitivas en Sudamérica y el mundo. eluniverso.com 2008/11/30. https://www.eluniverso.com/2008/11/30/0001/12/636B87E403CB41EE9A5A7FF5DAF79978.html

     

     

  • 1Eva_IT2005_T2 Valor de π por multiplicadores

    Parcial I Término 2005 - 2006. Julio 05, 2005 /ICM00794

    Tema 2. (30 puntos). El número π puede ser obtenido mediante la siguiente aproximación con un número n grande:

    pi por promedios serie

    Realice un algoritmo para encontrar el valor aproximado de π con la fórmula mostrada para n dado.

  • 1Eva_IT2005_T1 Prueba de escritorio, algoritmo

    Parcial I Término 2005 - 2006. Julio 05, 2005 /ICM00794

    Tema 1. (10puntos) Para el siguiente algoritmo, muestre la prueba de escritorio para encontrar el valor final de tr siendo los valores ingresados de vu=70 y ur=4.

    // Algoritmo
vu ← 0;
Mientras (vu<1)
    Ingrese (vu);
repita
ur ← 0;
Mientras (ur<1)
    ingrese (ur);
repita
tr ← 0;
mientras (ur<=vu)
    rc ← fix(vu/ur); //división entera vu/ur
    sb ← mod(vu,ur); //residuo división vu/ur
    tr ← tr+rc;
    vu ← rc+sb;
repita
mostrar (tr);
    Prueba de escritorio:
    vu ur tr rc sb
    .
    .
    ...... ..... ...... ..... .....

  • 1Eva_IIT2005_T1 Paridad y binario a decimal

    Parcial II Término 2005 - 2006. Diciembre 06, 2005 /ICM00794

    Tema 1. (20 puntos) Suponga un vector de n componentes.
    Almacene en cada celda un número aleatorio binario de una cifra.

    a) Determine si la cantidad de 1’s es par o impar
    b) Calcule y muestre el equivalente numérico decimal del número binario almacenado.

    Ejemplo:
    vector(i) 1 0 0 1 1 1 0 1

    cantidad de 1´s: impar
    Equivalente decimal: 15710

    vector = [1,0,0,1,1,1,0,1]

  • 1Eva_IIT2004_T4 Matriz de paridad

    Parcial II Término 2004 – 2005. Diciembre, 2004 /ICM00794

    Tema 4. (25 puntos) Se necesita transmitir una matriz de 7 filas y 7 columnas conteniendo “bits” (ceros o unos).

    Antes de transmitirla se debe agregar una columna a la derecha conteniendo ceros o unos, de tal manera que las 7 filas tengan paridad par, es decir que la cantidad de unos en cada fila sea par. Este cero o uno adicional se denomina bit de paridad.

    Realice un algoritmo que genere aleatoriamente la matriz de 7×7 llena con ceros y unos, agregue el bit de paridad en cada fila y muestre la matriz resultante.

    Ejemplo: Matriz
    Datos Paridad
    1 0 1 1 1 0 1 1
    0 1 0 1 1 0 1 0
    1 1 1 1 1 0 1 0
    1 0 1 1 0 1 1 1
    1 0 1 0 0 1 0 1
    1 0 1 0 0 0 1 0
    1 1 1 1 0 1 1 0

    Ejemplo:
    Para la primera fila: 1011101  1
    La suma de los primeros 7 bits es 5, que es un resultado impar.

    Para que la suma de toda la fila sea par se debe añadir un bit 1 adicional que es el bit de paridad.

    Si suma ahora los 8 bits, incluyendo el bit de paridad, el resultado es 6 que es un número par, cumpliendo así con lo requerido.

    Sugerencia: Resuelva primero para una fila, luego repita el resultado para las siguientes filas.
    Referencia:
    https://es.wikipedia.org/wiki/Paridad_(telecomunicaciones)

    matriz = [[1,0,1,1,1,0,1,1],
          [0,1,0,1,1,0,1,0],
          [1,1,1,1,1,0,1,0],
          [1,0,1,1,0,1,1,1],
          [1,0,1,0,0,1,0,1],
          [1,0,1,0,0,0,1,0],
          [1,1,1,1,0,1,1,0]]

  • 1Eva_IIT2004_T3 Estimar π por Montecarlo

    Parcial  II Término 2004 - 2005, Diciembre, 2004 /ICM00794

    Tema 3. (25 puntos) Encuentre un valor aproximado de la constante π con el siguiente procedimiento. circulo centrado en origen de radio 1

    Considere un círculo de radio unitario, centrado en el origen e inscrito en un cuadrado:

    Dado el valor n, genere las coordenadas x, y para n puntos.

    Asigne valores aleatorios reales entre 0 y 1 y cuente cuantos puntos caen dentro del cuadrante de círculo.

    Si llamamos a este contador k, se puede establecer la siguiente relación aproximada suponiendo n grande:

    \frac{k}{n} = \frac{\frac{1}{4} \text{del área del círculo}}{\frac{1}{4} \text{del área del cuadrado}} \frac{\frac{1}{4}\pi(1)^2}{\frac{1}{4} (2)^2}=\frac{\pi}{4} \frac{k}{n} =\frac{\pi}{4}

    Donde se puede obtener el valor aproximado de π a partir de k y n.

    Rúbrica: Puntos de coordenadas aleatorias dentro del cuadrado (5 puntos), verificar punto dentro del círculo (5 puntos), conteo de puntos dentro del círculo (5 puntos), calcular el valor de π (5 puntos). Algoritmo estructurado (5 puntos)

    Referencia:  Fontana di Trevi, https://es.wikipedia.org/wiki/Fontana_di_Trevi

  • 1Eva_IIT2004_T2 Apuestas a números con dados

    Parcial II Término 2004 – 2005. Diciembre, 2004 /ICM00794

    Tema 2. (25 puntos) Simule en un algoritmo el juego descrito entre dos personas: A y B. dado
    Muestre cuál jugador gana el juego y cuántos turnos se tuvieron que jugar.

    • Inicialmente cada una tiene $20
    • En cada turno se lanza un dado
    • Si sale 6 o 4, A gana $3 y B pierde $3
    • Si sale 2, ninguno gana ni pierde
    • Si sale 1, A pierde $6 y B gana $6
    • Si sale 3 o 5, A pierde $1 y B gana $1

    El juego termina cuando una de las dos personas pierde todo su dinero.