Ejercicio: 1Eva_IIT2007_T3 Garantías de prestamos IESS
[ algoritmo ] [ diagrama flujo ]
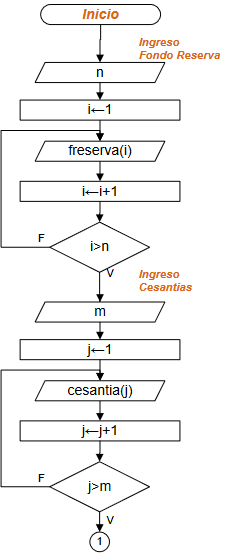
Para el ejemplo, por simplicidad se usan cédulas de 3 dígitos; también se supone que no existen elementos repetidos dentro de cada arreglo.
|
|
En la nota se indica que las listas de las cédulas de los afiliados tienen tamaño diferente, además el ingreso de datos es separado por tener origen de datos diferentes.
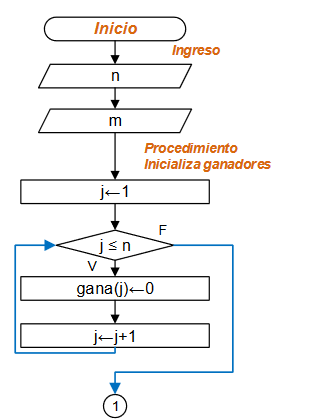
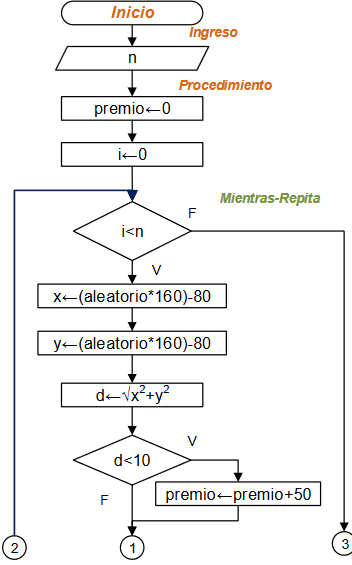
# INGRESO # datos de afiliados con fondo de reserva n = int(input('Afiliados con Fondo de Reserva: ')) freserva = np.zeros(n+1,dtype=int) i = 1 while not(i>n): print(i) freserva[i] = input('ingrese cedula:') i = i + 1
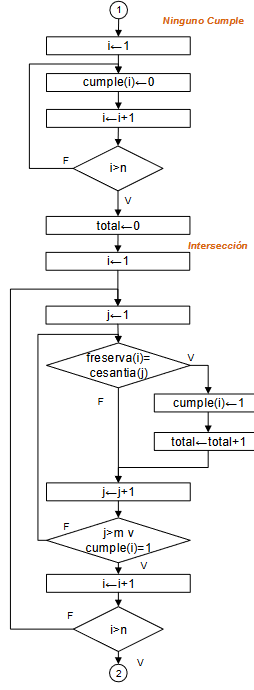
Al inicio del algoritmo, se supondrá que ningún afiliado cumple con los requisitos, por lo que se usa un arreglo de banderas de cumple o no cumple (1 ó 0).
# Hipotesis: Ninguno cumple requisito cumple = np.zeros(n+1,dtype=int)
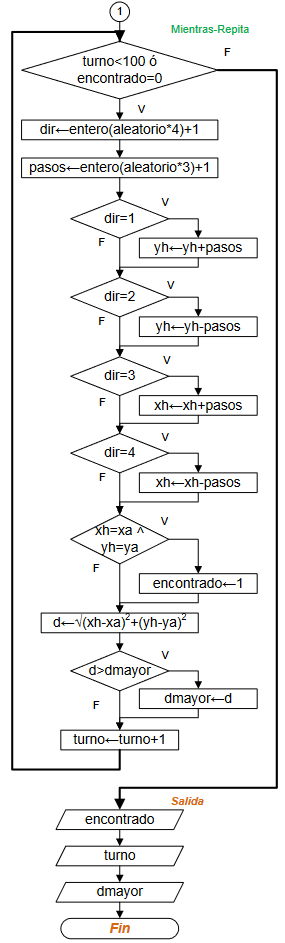
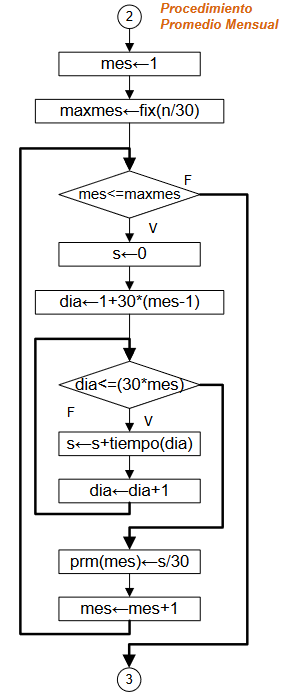
Realizar una búsqueda ordenada de números de cédula:
- para cada cédula de reserva[i] con n elementos
- realizar una búsqueda en el arreglo de cesantía[j] para los m elementos.
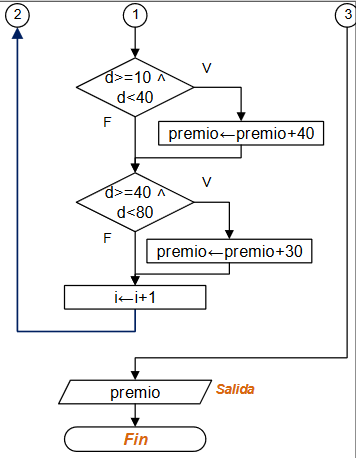
# Revisa listado buscando iguales total = 0 i = 1 while not(i>n): j = 1 while not(j>m or cumple[i]==1): if freserva[i]==cesantia[j]: cumple[i] = 1 total = total + 1 j = j + 1 i = i + 1
Repetir el proceso, marcando el arreglo de banderas, cumple, cada vez que se encuentra un valor repetido entre ambas listas.
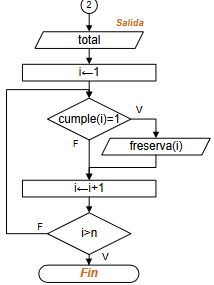
Tarea: Realizar el ejercicio, construyendo un tercer arreglo con solamente los elementos que cumplen con la condición.
[ algoritmo ] [ diagrama flujo ]
..
Algoritmo en Python
# ICM00794-Fundamentos de Computación - FCNM-ESPOL # 1Eva_IIT2007_T3 Garantías de prestamos IESS # propuesta: edelros@espol.edu.ec import numpy as np # INGRESO # datos de afiliados con fondo de reserva n = int(input('Afiliados con Fondo de Reserva: ')) freserva = np.zeros(n+1,dtype=int) i = 1 while not(i>n): print(i) freserva[i] = input('ingrese cedula:') i = i + 1 # datos de afiliados con cesantía m = int(input('Afiliados con Cesantia: ')) cesantia = np.zeros(m+1,dtype=int) j = 1 while not(j>m): print(j) cesantia[j] = input('ingrese cedula:') j = j + 1 # PROCEDIMIENTO # Hipotesis: Ninguno cumple requisito cumple = np.zeros(n+1,dtype=int) # Revisa listado buscando iguales total = 0 i = 1 while not(i>n): j = 1 while not(j>m or cumple[i]==1): if freserva[i]==cesantia[j]: cumple[i] = 1 total = total + 1 j = j + 1 i = i + 1 # SALIDA: Muestra cedulas de los que cumplen requisito print('Cumplen requisitos:') print(total) print('listado: ') i = 1 while not(i>n): if (cumple[i]==1): print(freserva[i]) i = i + 1
ejemplo de resultado del algoritmo
Afiliados con Fondo de Reserva: 3 1 ingrese cedula:123 2 ingrese cedula:234 3 ingrese cedula:345 Afiliados con Cesantia: 2 1 ingrese cedula:123 2 ingrese cedula:345 Cumplen requisitos: 2 listado: 123 345 >>>
[ algoritmo ] [ diagrama flujo ]
..
Diagrama de Flujo
[ algoritmo ] [ diagrama flujo ]
Propuesta de solución con diagrama de flujo, Python y otra versión con Matlab