Ejercicio: 1Eva_IIT2006_T2 Dígito verificador de cuenta

[ algoritmo n_dígitos ] [ diagrama flujo ] ; [ algoritmo 4_dígitos ]

Para números de cuenta con 4 dígitos y un verificador, se extrae el dígito verificador usando el residuo para 10; con el cociente de la división para 10 queda el número de cuenta como se indica en la descripción. Referencia, Operaciones básicas

Ejemplo

Código:	25431	codigo = 25431
verificador escrito:	1	escrito = codigo%10 = 25431 % 10 = 1
número de cuenta:	25431	numero = codigo//10 = 25431 // 10 = 2543

se extraen los dígitos del número de posición impar usando también el residuo de 10. Se continua la operación con el siguiente dígito usando la división entera de 10

impar  = numero%10 = 2543%10 = 3
numero = numero//10 = 2543//10 = 254

de forma semejante se obtiene el dígito de posición par, usando el residuo de 10.

par = numero%10 =254%10 = 4
numero = numero//10 = 254//10 = 25

Se continúa con las operaciones para los siguientes dígitos, realizando la operación de suma y multiplicación.

Se obtiene el verificador calculado para compararlo con el verificador recibido, estableciendo si la respuesta es afirmativa o negativa.

[ algoritmo n_dígitos ] [ diagrama flujo ] ; [ algoritmo 4_dígitos ]
..

---

Algoritmo en Python: para n dígitos

Opción 1. Usando lazos, es más general para usar mayor cantidad de dígitos

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2006_T2 Dígito verificador de cuenta

# INGRESO
codigo = int(input('escriba el codigo completo: '))

# PROCEDIMIENTO
escrito = codigo%10
numero  = codigo//10

multimpar = 1
sumapar   = 0
while not(numero <= 0):
    impar  = numero%10
    numero = numero//10
    multimpar = multimpar*impar

    par = numero%10
    numero  = numero//10
    sumapar = sumapar+par
    
suma = sumapar + multimpar
calculado = suma%10

if (escrito == calculado):
    respuesta = 1
else:
    respuesta = 0

# SALIDA
print(respuesta)

[ algoritmo n_dígitos ] [ diagrama flujo ] ; [ algoritmo 4_dígitos ]
..

---

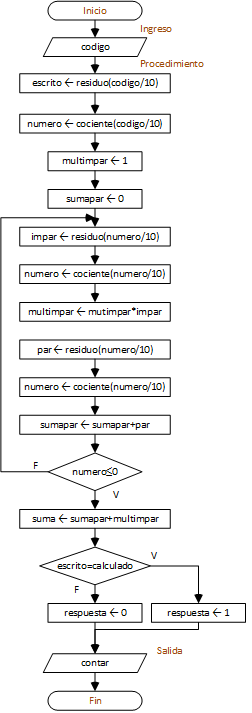
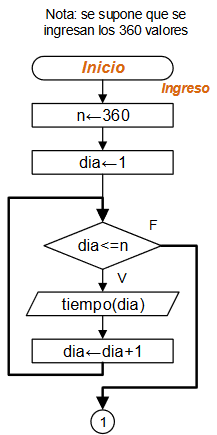
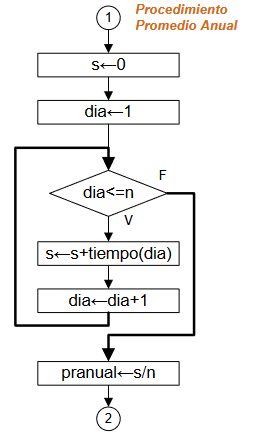
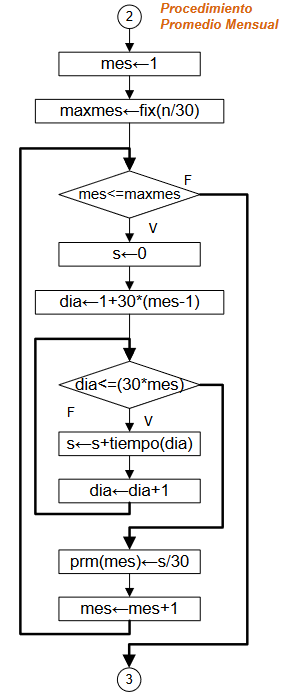
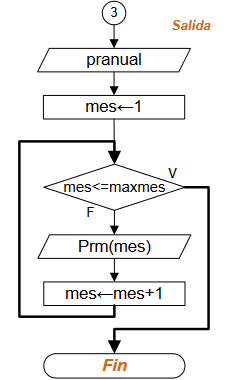
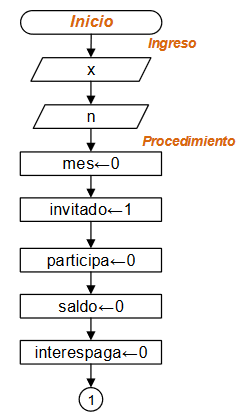
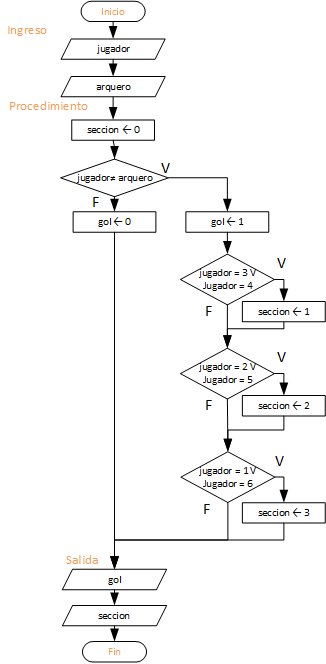
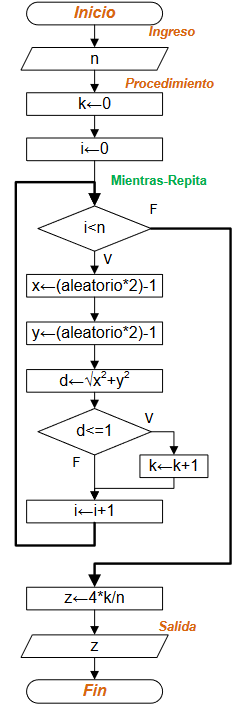
Diagrama de Flujo

Ejecución del algoritmo

escriba el codigo completo: 25431
1
>>> 
escriba el codigo completo: 25432
0
>>> 

[ algoritmo n_dígitos ] [ diagrama flujo ] ; [ algoritmo 4_dígitos ]
..

---

Algoritmo en Python: para 4 dígitos

Opción 2. En caso que requiera repasar más sobre lazos, aún se presenta una solución particular, solo para cuatro dígitos.

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1ra Evaluación II Termino 2006
# Tema 2. Verificador cuenta. Ejercicio Básico

# INGRESO
codigo = int(input('escriba el codigo completo: '))

# PROCEDIMIENTO
escrito = codigo%10
numero = codigo//10

a = numero%10
numero = numero//10

b = numero%10
numero = numero//10

c = numero%10
d = numero//10

suma = a*c+(b+d)
calculado = suma%10

if (escrito == calculado):
    respuesta = 1
else:
    respuesta = 0

# SALIDA
print(respuesta)

[ algoritmo n_dígitos ] [ diagrama flujo ] ; [ algoritmo 4_dígitos ]

Propuesta de solución en Python, otras propuestas:

ejercicios resueltos Python 1eva_iit2006_t2 pdf

ejercicios resueltos Matlab 1eva_iit2006_t2 pdf

Ejercicio: 1Eva_IIT2005_T4 Juego escaleras y serpientes

Algoritmo: [ mientras-repita ] [ repita-hasta ] ; [ diagrama flujo ]

En un primer bosquejo, no se considera el lanzar la moneda para ver cuál jugador inicia, semejante al ajedrez en que las fichas blancas salen primero sin considerar el nombre del jugador.

Para determinar las posiciones de las fichas en el tablero, se usarán acumuladores para cada jugador A y B, usando como variables “fichaa” y “fichab”.

# jugador A
dadoa = int(rnd.random()*6)+1
fichaa = fichaa + dadoa

Serán necesarios otras variables como el contador para el turno, cada jugador dispondrá de una variable generada de forma aleatoria dadoa, dadob, que simula un dado de 6 caras.

Se lanza el dado para el jugador A, se avanza acumulando conforme a los puntos del dado, se valida el premio o castigo para luego repetir el proceso para el jugador B, repitiendo el proceso hasta que alguna ficha se ubique o pase la casilla de “llegada”.

    if (fichaa==4 or fichaa==9 or fichaa==29 or fichaa==34 or fichaa==46):
        fichaa = fichaa + 3
    if (fichaa==8 or fichaa==19 or fichaa==38 or fichaa==50 or fichaa==60):
        fichaa = fichaa - 3

Terminado el proceso anterior, se determina cuál jugador ganó, observe que se supone que gana tiene inicialmente el valor de 0, para tener la opción de registrar un empate.

Al final se muestran los resultados del juego simulado.

Tarea: Resolver con el lanzamiento de la moneda para ver cuál inicia.

Algoritmo: [ mientras-repita ] [ repita-hasta ] ; [ diagrama flujo ]

..

---

Algoritmo en Python: Mientras-Repita

Primero se presenta la solución usando lazo “Mientras-Repita”, luego se muestra la versión con el lazo “Repita-Hasta” que se puede escribir en otros lenguajes de programación.

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2005_T4 Juego escaleras y serpientes
# Propuesta de solución: edelros@espol.edu.ec

import random as rnd

# INGRESO
# Sortear quién empieza

# PROCEDIMIENTO
llegada = 64
fichaa = 0
fichab = 0

turno = 0
while (fichaa<llegada or fichab<llegada):

    # jugador A
    dadoa = int(rnd.random()*6)+1
    fichaa = fichaa + dadoa
    if (fichaa==4 or fichaa==9 or fichaa==29 or fichaa==34 or fichaa==46):
        fichaa = fichaa + 3
    if (fichaa==8 or fichaa==19 or fichaa==38 or fichaa==50 or fichaa==60):
        fichaa = fichaa - 3

    #jugador B
    dadob = int(rnd.random()*6)+1
    fichab = fichab + dadob
    if (fichab==4 or fichab==9 or fichab==29 or fichab==34 or fichab==46):
        fichab = fichab + 3
    if (fichab==8 or fichab==19 or fichab==38 or fichab==50 or fichab==60):
        fichab = fichab - 3

    turno = turno + 1

# Revisa ganador
gana = 0
if fichaa > fichab:
    gana = 1
if fichab > fichaa:
    gana = 2

# SALIDA
print('gana el jugador: ')
print(gana)
print('turnos jugados:')
print(turno)

Ejecución del algoritmo

gana el jugador: 
2
turnos jugados:
16
>>> 
gana el jugador: 
2
turnos jugados:
16
>>> 

Algoritmo: [ mientras-repita ] [ repita-hasta ] ; [ diagrama flujo ]
..

---

Algoritmo en Python: Repita-Hasta

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2005_T4 Juego escaleras y serpientes
# Propuesta de solución. edelros@espol.edu.ec

import random as rnd

# INGRESO
# Sortear quién empieza 
# PROCEDIMIENTO

llegada = 64
fichaa = 0
fichab = 0

turno = 0
while not(fichaa>=llegada or fichab>=llegada):

    # jugador A
    dadoa = int(rnd.random()*6)+1
    fichaa = fichaa+dadoa
    if (fichaa==4 or fichaa==9 or fichaa==29 or fichaa==34 or fichaa==46):
        fichaa = fichaa+3
    if (fichaa==8 or fichaa==19 or fichaa==38 or fichaa==50 or fichaa==60):
        fichaa = fichaa - 3

    #jugador B
    dadob = int(rnd.random()*6)+1
    fichab = fichab + dadob
    if (fichab==4 or fichab==9 or fichab==29 or fichab==34 or fichab==46):
        fichab = fichab + 3
    if (fichab==8 or fichab==19 or fichab==38 or fichab==50 or fichab==60):
        fichab = fichab - 3

    turno = turno+1

gana = 0
if fichaa>fichab:
    gana = 1

if fichab>fichaa:
    gana = 2

# SALIDA
print('gana el jugador: ')
print(gana)
print('turnos jugados:')
print(turno)

Algoritmo: [ mientras-repita ] [ repita-hasta ] ; [ diagrama flujo ]
..

---

Diagrama de Flujo

 

Algoritmo: [ mientras-repita ] [ repita-hasta ] ; [ diagrama flujo ]

Propuesta de solución:

ejercicios resueltos Python parc_iit2005_t4 pdf

ejercicios resueltos Matlab parc_iit2005_t4 pdf

Ejercicio: 1Eva_IIT2005_T3 Entrenamiento atleta: promedios

[ algoritmo ] [ diagrama flujo ]

Pedir la cantidad de mediciones n a tabular

n = int(input('¿días a cronometrar?: '))

Ingresar todos los tiempos en un arreglo de n elementos.

# Inicia tabla de tiempos
tiempo = np.zeros((n+1),dtype=int)
dia = 1
while (dia<=n):
    print('tiempo[' + str(dia) + ']: ')
    tiempo[dia] = float(input(''))
    dia = dia + 1

Empezar con el promedio anual, acumular en s todos los tiempos.

# Promedio anual
s = 0
dia = 1
while (dia<=n):
    s = s + tiempo[dia]
    dia = dia+1

El promedio anual se obtiene con la suma s al dividirla para n.

pranual = s/n

Para el promedio mensual, desarrollar el algoritmo para el primer mes (día 1 al 30) y luego revisar la relación que existe entre el primer día del mes y el número del mes, revisar también para el último día del mes.

Determinar la relación también para los días de la semana y el número de la semana, comparar resultados.

Tarea: completar el algoritmo, pues la solución propuesta no desarrolla el promedio semanal.

En el caso de Python, es necesario declarar el vector, al menos con valores de 0. Como la primera posición del arreglo es 0 y no existe el día 0, se aumentará el tamaño del vector en 1, a fin de usar el indicador de día de forma más natural.

Se requiere importar la librería Numpy, para trabajar con los arreglos.

[ algoritmo ] [ diagrama flujo ]
..

---

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2005_T3 Entrenamiento atleta: promedios
# Propuesta de solución. edelros@espol.edu.ec
# Tarea: realizar promedio por semana

import numpy as np

# INGRESO
n = int(input('¿días a cronometrar?: '))

# Inicia tabla de tiempos
tiempo = np.zeros((n+1),dtype=int)
dia = 1
while (dia<=n):
    print('tiempo[' + str(dia) + ']: ')
    tiempo[dia] = float(input(''))
    dia = dia + 1

# PROCEDIMIENTO

# Promedio anual
s = 0
dia = 1
while (dia<=n):
    s = s + tiempo[dia]
    dia = dia+1
pranual = s/n

# Promedio mensual
mes = 1
maxmes = int(n/30)
while (mes<=maxmes):
    s = 0
    dia = 1+30*(mes-1)
    while (dia<=(30*mes)):
        s = s+tiempo[dia]
        dia = dia+1
    prm[mes] = s/30
    mes = mes+1

# SALIDA
print('Promedio anual: ')
print(pranual)
print('Promedio mensual: ')
mes = 1
if maxmes==0:
    print('Meses completos: 0')
while (mes<=maxmes):
    print(prm[mes])
    mes = mes+1

# Se modificó el algoritmo para
# probar con n de pocos días.

Ejecución del algoritmo

¿días a cronometrar?: 5
tiempo[1]: 
20
tiempo[2]: 
18
tiempo[3]: 
23
tiempo[4]: 
19
tiempo[5]: 
22
Promedio anual: 
20.4
Promedio mensual: 
Meses completos: 0
>>> 

[ algoritmo ] [ diagrama flujo ]
..

---

Diagrama de Flujo

[ algoritmo ] [ diagrama flujo ]

Propuesta de solución en Python, también en Matlab:

ejercicios resueltos Python parc_iit2005_t3 pdf

ejercicios resueltos Matlab parc_iit2005_t3 pdf

Ejercicio: 1Eva_IIT2005_T2 Negocio piramidal

[ algoritmo ] [ diagrama flujo ]

Para la solución, considere las operaciones descritas en el orden lógico de ejecución: depósitos, comisiones e intereses pagados para calcular el saldo.

siendo x la cantidad de depositantes.

deposito = invitado*x
comision = 0.20*deposito
interespaga = 0.10*x*participa
saldo = saldo+deposito-comision-interespaga
participa = participa+invitado

El control de participantes e invitados permitirá calcular apropiadamente los depósitos de los invitados y los intereses pagados a los participantes.

Los meses se cuentan para cada iteración hasta que se cumpla la condición que los intereses pagados sean mayores al saldo.

while (interespaga<=saldo):

[ algoritmo ] [ diagrama flujo ]
..

---

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2005_T2 Negocio piramidal
# Propuesta de solución: edelros@espol.edu.ec

# INGRESO
x = int(input('cantidad por depositante: '))
n = int(input('personas en el mercado: '))

# PROCEDIMIENTO
mes = 0
invitado = 1
participa = 0

saldo = 0
interespaga = 0
while (interespaga<=saldo):
    deposito = invitado*x
    comision = 0.20*deposito
    interespaga = 0.10*x*participa
    saldo = saldo+deposito-comision-interespaga
    participa = participa+invitado

    if (participa<=(n/2)):
        invitado = participa
    else:
        invitado = 0
    
    mes = mes+1

# SALIDA
print('meses con saldo disponible: ')
print(mes)

Ejecución del algoritmo

cantidad por depositante: 100
personas en el mercado: 1000
meses con saldo disponible: 
17
>>>

[ algoritmo ] [ diagrama flujo ]
..

---

Diagrama de Flujo

[ algoritmo ] [ diagrama flujo ]

Propuesta de solución en Python, también en Matlab:

ejercicios resueltos Python parc_iit2005_t2 py_pdf

ejercicios resueltos Matlab parc_iit2005_t2 pdf

Ejercicio: 1Eva_IT2005_T4 Lanza penales

[ algoritmo ] [ diagrama flujo ]

Propuesta de solución en Python. 

Se realiza el control de goles conseguidos en cada lanzamiento de balón, contando los lanzamientos hasta que se alcancen 5 .

conseguido = 0
lanza = 0
while not(lanza==5):

El área dónde patea el balón el jugador se ingresa por teclado y la posición del arquero se obtiene de un aleatorio.

    # Patea
    print('Penal número: ', lanza)
    patea = int(input('donde patea: '))
    while not(patea>=1 and patea<=6):
        patea = int(input('OE!..donde patea: '))

    # Arquero
    arquero = int(rnd.random() * 6) +1

Se analiza si hubo gol siempre que donde se patea sea diferente donde está el arquero, con lo que se contabiliza los goles conseguidos.

    # Gol/tapa
    if not(patea==arquero):
        gol = 1
    else:
        gol = 0

    conseguido = conseguido + gol
    lanza = lanza + 1

[ algoritmo ] [ diagrama flujo ]
..

---

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2005_T4 Lanza penales

import random as rnd

conseguido = 0
lanza = 0
while not(lanza==5):

    # Patea
    print('Penal número: ', lanza)
    patea = int(input('donde patea: '))
    while not(patea>=1 and patea<=6):
        patea = int(input('OE!..donde patea: '))

    # Arquero
    arquero = int(rnd.random() * 6) +1

    # Gol/tapa
    if not(patea==arquero):
        gol = 1
    else:
        gol = 0

    conseguido = conseguido + gol
    lanza = lanza + 1

    # Resultado
    print('patea, arquero, gol/tapa')
    print(patea, arquero, gol)

print('*** Goles conseguidos: ', conseguido)

Ejemplo de resultado del algoritmo:

Penal número:  0
donde patea: 3
patea, arquero, gol/tapa
3 3 0
Penal número:  1
donde patea: 2
patea, arquero, gol/tapa
2 6 1
Penal número:  2
donde patea: 1
patea, arquero, gol/tapa
1 1 0
Penal número:  3
donde patea: 2
patea, arquero, gol/tapa
2 4 1
Penal número:  4
donde patea: 3
patea, arquero, gol/tapa
3 5 1
*** Goles conseguidos:  3
>>>

[ algoritmo ] [ diagrama flujo ]
..

---

Diagrama de Flujo

[ algoritmo ] [ diagrama flujo ]

Ejercicio: 1Eva_IT2005_T3 Arreglo aleatorio binario a decimal

Propuesta de solución en Python

Use un vector de n casillas,

Las casillas pueden iniciar en cero,para luego llenarlas de números aleatorios una por una,

B = np.zeros(n,dtype=int)

Junto a la operación anterior, podría realizar las operaciones requeridas en el enunciado.

B[i] = int(rnd.random()*2)+0

De ser necesario repasar: Binario a Decimal – Algoritmo

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2005_T3 Arreglo aleatorio binario a decimal
# Tarea: contar los 1's, literal a)

import numpy as np
import random as rnd

# INGRESO
n = int(input('cuantos componentes n: '))

# PROCEDIMIENTO
B = np.zeros(n,dtype=int)
decimal = 0
i = 0
while (i<n):
    B[i] = int(rnd.random()*2)+0
    # orden de binarios es izquierda a derecha
    posicion = n-1-i  
    decimal  = decimal+B[i]*(2**posicion)
    i = i+1

# SALIDA
print('Arreglo de binarios B[i]:')
print(B)
print('equivale en decimal:',decimal)

Resultados de algoritmo realizados para un byte (8 bits):

cuantos componentes n: 8
Arreglo de binarios B[i]:
[0 0 1 0 1 0 1 0]
equivale en decimal: 42
>>> 
cuantos componentes n: 8
Arreglo de binarios B[i]:
[1 1 1 1 1 1 1 1]
equivale en decimal: 255
>>> 
cuantos componentes n: 8
Arreglo de binarios B[i]:
[0 0 1 1 1 1 1 0]
equivale en decimal: 62
>>> 

Ejercicio: 1Eva_IIT2004_T4 Matriz de paridad

Establecer una matriz de n filas y n+1 columnas.

matriz = np.zeros(shape=(n,n+1),dtype=int)

Para cada casilla en cada fila y columna, generar un aleatorio de dos posibilidades que mínimo puede ser cero.

aleatorio = int(rnd.random()*2)+0

con lo que se genera la matriz de números aleatorios.

Al finalizar una fila, considere la suma de fila para revisar la paridad con el residuo de la división para 2.

    residuo = sumafila % 2

Si hay residuo el número es impar y se debe escribir el número 1 en la última casilla de toda la fila (fila, n), es decir se completa la paridad.

En el caso opuesto, que no hay residuo=0, el conteo de '1' ya es par y se deja el valor cero en la última casilla.

Algoritmo en Python

# 1Eva_IIT2004_T4 Matriz de paridad
import numpy as np
import random as rnd

# INGRESO
n = 7 # tamaño matriz

# PROCEDIMIENTO
# matriz de n filas y n+1 columnas
matriz = np.zeros(shape=(n,n+1),dtype=int)

# recorre matriz
for fila in range(0,n,1):
    sumafila = 0
    for columna in range(0,n,1):
        aleatorio = int(rnd.random()*2)+0
        matriz[fila,columna] = aleatorio
        sumafila = sumafila + aleatorio
    # revisa residuo paridad
    residuo = sumafila % 2  
    if residuo: # sumafila es impar
        matriz[fila,n] = 1

# SALIDA
print(' Matriz obtenida')
print(matriz)

resultado:

 Matriz obtenida
[[0 1 1 1 0 1 1 1]
 [1 1 0 1 0 0 1 0]
 [0 1 1 1 0 1 1 1]
 [1 0 0 1 1 0 1 0]
 [0 1 0 0 0 1 0 0]
 [1 0 0 0 1 1 0 1]
 [1 0 0 0 1 0 1 1]]
>>> 

Nota: Observe que la matriz contiene números aleatorios, por lo que el resultado varía cada vez que se ejecuta el algoritmo.

Ejercicio: 1Eva_IIT2004_T3 Estimar π por Montecarlo

[ algoritmo ] [ diagrama flujo ]

Ingresar la cantidad de puntos n para ubicar en el plano de forma aleatoria dentro del rango del cuadrado que contiene al círculo. 

Usar una variable k como el contador para los puntos que caen dentro del círculo.

Al generar aleatoriamente cada punto (x,y), se puede calcular la distancia al centro usando Pitágoras.

d= \sqrt{x^2 +y^2}

Se repite el proceso para n puntos y al final se calcula el valor estimado de pi según la relación del enunciado.

\frac{k}{n} =\frac{\pi}{4}

Nota: no se usa como variable la palabra “pi” debido a que es nombre de variable reservada.

[ algoritmo ] [ diagrama flujo ]
..

---

Algoritmo en Python

# 1Eva_IIT2004_T3 Estimar Pi por Montecarlo
# Propuesta de solución. edelros@espol.edu.ec
# se usa todo el círculo
import random as rnd
import numpy as np

# INGRESO
n = int(input('¿Cuántos puntos?: '))
radio = 1

# PROCEDIMIENTO
punto = np.zeros(shape=(n,2),dtype=float)
k = 0
i = 0
while i<n:
    x = rnd.random()*(2*radio)-1
    y = rnd.random()*(2*radio)-1

    d = np.sqrt(x**2+y**2)
    if d<=radio:
        k = k + 1
    punto[i] = [x,y]
    i = i + 1

estimadopi = 4*k/n

# SALIDA
print(k,n)
print('estimador pi: ', estimadopi)
print(punto)

la estimación de π con números aleatorios que se ubican dentro del círculo de radio 1 es:

¿Cuántos puntos?: 1000
781 1000
estimador pi:  3.124
[[ 0.15581724  0.43992571]
 [-0.11114653 -0.86426905]
 [ 0.51257751 -0.1969925 ]
 ...
 [ 0.26965478 -0.01555604]
 [-0.89575602  0.56077385]
 [ 0.33467618 -0.59497405]]
>>> 

[ algoritmo ] [ diagrama flujo ]
..

---

Diagrama de Flujo

[ algoritmo ] [ diagrama flujo ]

ejercicios resueltos Matlab parc_iit2004_t3 pdf

Ejercicio: 1Eva_IT2004_T3 Sortear parejas para tenis

Propuesta de solución en Python:

La variable n indica el número de parejas o tamaño de los vectores para almacenar la "pareja" y el contador de "veces" que juega cada una.

# INGRESO
n = int(input('cuantas parejas: '))

El ejercicio se divide en dos partes: la primera para seleccionar de forma aleatoria la pareja de la dama (una por una), es decir se sortean los caballeros (quien), y la segunda parte se realiza el proceso para los caballeros.

dama = n+1
while not(dama>(2*n)):
    quien = int(rnd.random()*n)+1
    pareja[dama] = quien
    veces[quien] = veces[quien]+1
    dama = dama + 1

En cada sorteo se registra cuántas veces participa cada uno.

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2004_T3 Sortear parejas para tenis

import random as rnd
import numpy as np

# INGRESO
n = int(input('cuantas parejas: '))

# PROCEDIMIENTO
pareja = np.zeros(2*n+1,dtype=int)
veces  = np.zeros(  n+1,dtype=int)

dama = n+1
while not(dama>(2*n)):
    quien = int(rnd.random()*n)+1
    pareja[dama] = quien
    veces[quien] = veces[quien]+1
    dama = dama + 1

# SALIDA
print(pareja[n+1:])
print('veces: ')
print(veces)

print('juegan varias veces: ')
caballero = 1
while not(caballero>n):
    if (veces[caballero]>1):
        print(caballero)
    caballero = caballero + 1

print('los que no juegan: ')
caballero = 1
while not(caballero>n):
    if (veces[caballero]==0):
        print(caballero)
    caballero = caballero + 1

con un ejemplo de resultado:

cuantas parejas: 10
[ 6  2  1  8  3  9 10  1  7  9]
veces: 
[0 2 1 1 0 0 1 1 1 2 1]
juegan varias veces: 
1
9
los que no juegan: 
4
5
>>> 

Ejercicio: 1Eva_IT2004_T2 Verificar ISBN

Propuesta de solución en Python, para un número ISBN dado

ISBN = 9684443242

Luego de pedir el número ISBN, se inicia extrayendo el dígito verificador escrito, quedando el resto de dígitos del número hacia la izquierda para realizar los cálculos.

vescrito = ISBN%10
n = ISBN//10

Tarea: verificar el número de dígitos del ISBN

Para la posición del dígito se usa un contador.

Las operaciones se acumulan en suma, de la que se obtiene el residuo de la división para 11.

El residuo corresponde al verificador calculado que se compara con el verificador escrito para dar el veredicto.

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2004_T2 Verificar ISBN
# propuesta: edelros@espol.edu.ec

# INGRESO
ISBN = int(input('cual ISBN: '))

# PROCEDIMIENTO
vescrito = ISBN%10
n = ISBN//10

contador = 9
suma = 0
while (n>0):
    digito = n%10
    n = n//10
    suma =  suma + digito*contador
    contador = contador -1

vcalculado = suma%11

if (vescrito==vcalculado):
    respuesta = 1
else:
    respuesta = 0

#SALIDA
print(respuesta)

Resultado del algoritmo

cual ISBN: 9684443242
1
>>> 
cual ISBN: 9684443243
0
>>>