Ejercicio: 1Eva_IT2014_T2 Verificar EAN

[ algoritmo ] [ diagrama flujo ]

Para un número EAN dado, de cualquier producto, se ingresa como un número entero.

 

# INGRESO
EAN = int(input('European Article Number,EAN: '))

Se requiere separar los componentes usando cociente y residuo: producto, empresa y país según las posiciones y cantidad de dígitos.

# PROCEDIMENTO
# separar las partes
verificador = EAN%10 # un dígito
numero = EAN//10

producto = numero%100000 # cinco dígitos
numero =  numero//100000

empresa =  numero%10000 # cuatro dígitos
pais =  numero//10000

Luego encontrar la suma de los dígitos con la operación indicada en el enunciado.

La siguiente semana de ser necesario se explica el tema de la decena superior.

[ algoritmo ] [ diagrama flujo ]

..

---

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2014_T2 Verificar EAN

# INGRESO
EAN = int(input('European Article Number,EAN: '))

# PROCEDIMENTO
# separar las partes
verificador = EAN%10  # un dígito
numero = EAN//10

producto = numero%100000 # cinco dígitos
numero =  numero//100000

empresa =  numero%10000  # cuatro dígitos
pais =  numero//10000

# calcular verificador
suma = 0
numero = numero = EAN//10
while not(numero<=0):
    digito = numero%10
    numero = numero//10
    suma   = suma + 3*digito
    
    digito = numero%10
    numero = numero//10
    suma   = suma + 1*digito
    
decena    = suma//10
superior  = (decena + 1)*10
calculado = superior - suma

if (verificador == calculado):
    valido = 1
else:
    valido = 0
    
# SALIDA
print('el numero ingresado es válido: ', valido)
print('producto: ', producto)
print('empresa: ', empresa)
print('pais: ', pais)

resultado del algoritmo

European Article Number,EAN: 7702004003508
el numero ingresado es válido:  1
producto:  350
empresa:  2004
pais:  770
>>> 

European Article Number,EAN: 7702004003509
el numero ingresado es válido:  0
producto:  350
empresa:  2004
pais:  770
>>> 

[ algoritmo ] [ diagrama flujo ]
..

---

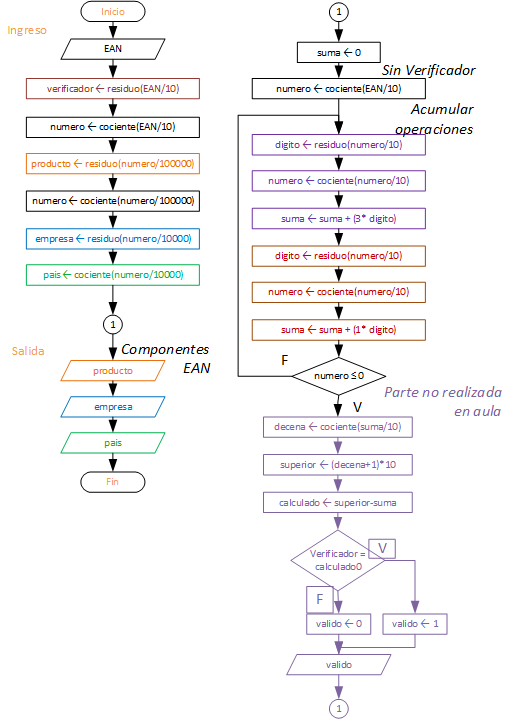
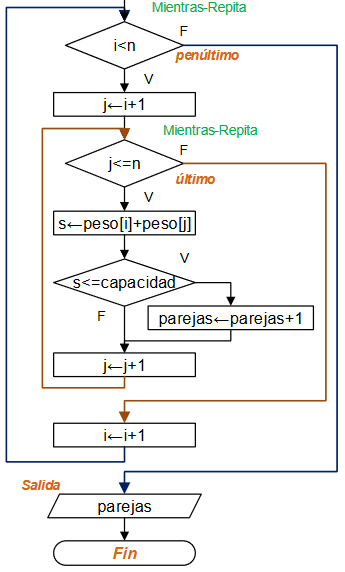
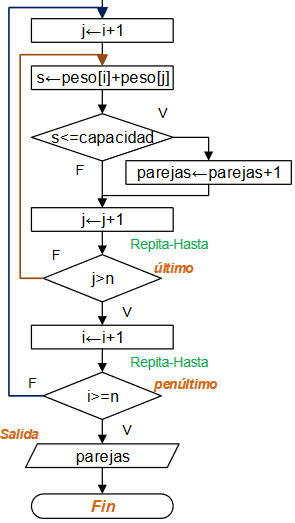
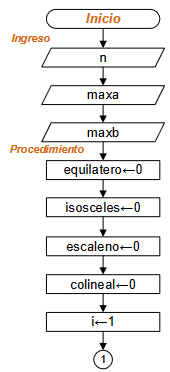
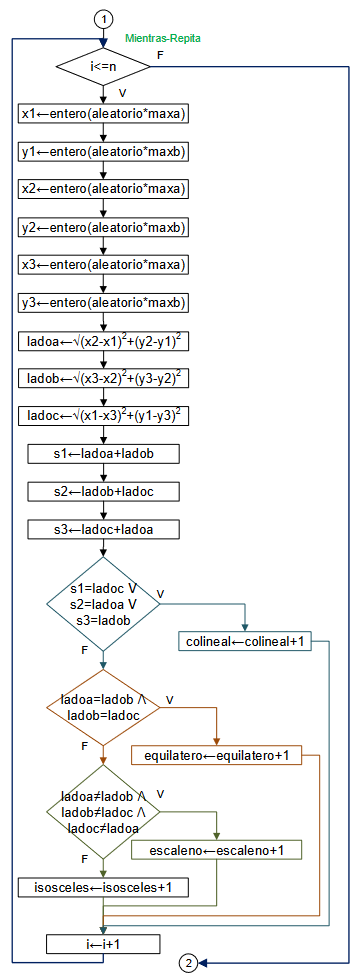
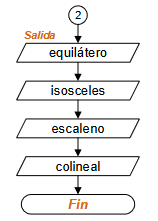
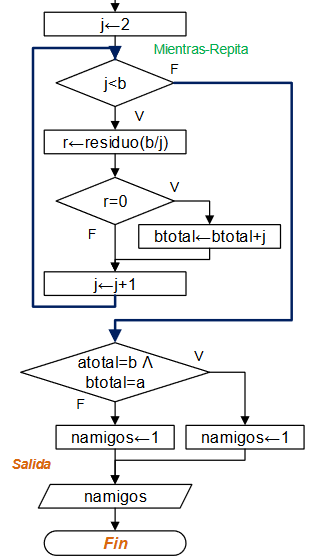
Diagrama de Flujo

Diagrama según taller realizado en aula. tenía una sección de tarea.

[ algoritmo ] [ diagrama flujo ]

Ejercicio: 1Eva_IIT2014_T4 Turnos en imprenta de gigantografía

Propuesta de solución en el Archivo diagrama en pdf

Tarea: traducir el diagrama a instrucciones en Python

 

ejercicios resueltos Python 1eva_iit2014_t4 pdf

Ejercicios: 1Eva_IIT2014_T3 Parasailing sin sobrecarga, parejas

[ algoritmo ] diagrama flujo: [ mientras-repita ] [ repita-hasta ]

El ejercicio consiste en una revisión ordenada del peso de cada persona a participar con una posible pareja.

i	1	2	3	...
pesos[i]	120	180	165	...

Los pesos de cada persona se registran en un arreglo.

# INGRESO
capacidad = int(input('capacidad de equipo: '))
n = int(input('personas en cola: '))

peso = np.zeros((n+1),dtype=int)
i = 1
while (i<=n):
    peso[i] = int(input("Peso[ "+str(i)+"]:"))
    i = i + 1

El algoritmo comienza revisando una persona i junto a otra persona j. Si la pareja no sobrecarga el paracaidas, se cuenta y registra la pareja posible de participar en un solo viaje de parasailing.

        s = peso[i] + peso[j]

        # revisa capacidad
        if (s<=capacidad):
            parejas = parejas + 1
            posibles.append([i,j])

Use un contador y una lista para el registro.

[ algoritmo ] diagrama flujo: [ mientras-repita ] [ repita-hasta ]
..

---

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2014_T3 Parasailing sin sobrecarga, parejas
# propuesta solucion: edelros@espol.edu.ec

import numpy as np

# INGRESO
capacidad = int(input('capacidad de equipo: '))
n = int(input('personas en cola: '))

peso = np.zeros((n+1),dtype=int)
i = 1
while (i<=n):
    peso[i] = int(input("Peso[ "+str(i)+"]:"))
    i = i + 1

# PROCEDIMIENTO

# busca parejas
posibles = []
parejas = 0
i = 1
while (i<n):
    j = i + 1
    while (j<=n):
        s = peso[i] + peso[j]

        # revisa capacidad
        if (s<=capacidad):
            parejas = parejas + 1
            posibles.append([i,j])
        
        j = j + 1
    i = i + 1

# SALIDA
print('La cantidad de parejas encontradas es: ')
print(parejas)
print('Se puede combinar: ')
print(posibles)

resultado del algoritmo

capacidad de equipo: 350
personas en cola: 3
Peso[ 1]:120
Peso[ 2]:180
Peso[ 3]:165
La cantidad de parejas encontradas es: 
3
Se puede combinar: 
[[1, 2], [1, 3], [2, 3]]
>>> 
capacidad de equipo: 300
personas en cola: 3
Peso[ 1]:120
Peso[ 2]:180
Peso[ 3]:165
La cantidad de parejas encontradas es: 
2
Se puede combinar: 
[[1, 2], [1, 3]]
>>> 

[ algoritmo ] diagrama flujo: [ mientras-repita ] [ repita-hasta ]
..

---

Diagrama de Flujo: Mientras-Repita

[ algoritmo ] diagrama flujo: [ mientras-repita ] [ repita-hasta ]
..

---

Diagrama de Flujo: Repita-Hasta

[ algoritmo ] diagrama flujo: [ mientras-repita ] [ repita-hasta ]

---

ejercicios resueltos Python 1eva_iit2014_t3 pdf

Ejercicio: 1Eva_IT2014_T1 Cuadrado de Cinco

Propuesta de solución en Python

Operación	decena	decena+1	añadir	resultado
252	2	2+1=3	2*3 = 6	625
852	8	8+1=9	8*9 = 72	7225

Para validar la operación con los múltiplos de 5 menores que 100, se usa un intervalo entre [5,m]. El intervalo inicia con el número 5

El siguiente número ascendente terminado en cinco es el anterior sumando 10.

La decena del número se obtiene como el cociente de la división para 10

El número por añadir a la izquierda de 25 es es la multiplicación de:
(decena)*](decena+1), que equivale a las centenas.

Para revisar que se cumpla la operación en todo el intervalo [5,m] se usa una bandera "funciona".

---

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2014_T1 Cuadrado de Cinco
# Tarea: validar que la unidad del número sea 5

# INGRESO
m = int(input('rango [5,m]: '))

# PROCEDIMIENTO
numero = 5 # inicial
funciona = True # si funciona
while (numero<=m and funciona==True):
    
    # terminados en 5 desde el 15
    numero = numero+10

    # algoritmo cuadrado de 5
    unidad = numero%10    #residuo
    decena = numero//10   #cociente
    a = decena*(decena + 1)
    propuesto = a*100 + 25

    # calcula cuadrado
    calculado = numero*numero

    #compara resultado
    if (calculado!=propuesto):
        funciona = False

# SALIDA
print ('Algoritmo funciona:',funciona)
if (funciona==0):
    print(numero)

resultado del algoritmo dentro del intervalo.

rango [5,m]: 100
Algoritmo funciona: True
>>> 
rango [5,m]: 1000
Algoritmo funciona: True
>>> 

Ejercicios: 1Eva_IIT2014_T2 Triángulos aleatorios en rectángulo

[ algoritmo ] [ diagrama flujo ]

Para iniciar el ejercicio, se requiere la cantidad n de triángulos a generar y los límites del plano donde se generan [maxa,maxb] .

Para cada triángulo se generan las coordenadas de los vértices (xi,yi), usando números aleatorios ajustados a los límites del plano.

    # puntos aleatorios
    x1 = int(rnd.random()*maxa) +0
    y1 = int(rnd.random()*maxb) +0
    
    x2 = int(rnd.random()*maxa) +0
    y2 = int(rnd.random()*maxb) +0

    x3 = int(rnd.random()*maxa) +0
    y3 = int(rnd.random()*maxb) +0

Lo más importante para este ejercicio es determinar las distancias entre los vértices, pues con ellas se determina el tipo de triángulo, siguiento las reglas básicas de la geometría.

    # distancias entre puntos
    a = np.sqrt((x2-x1)**2 + (y2-y1)**2)
    b = np.sqrt((x3-x2)**2 + (y3-y2)**2)
    c = np.sqrt((x1-x3)**2 + (y1-y3)**2)

Puede darse el caso que los puntos se encuentren en una sola línea en el plano, el caso se verifica al revisar si la suma de la longitud de dos lados es la longitud del tercer lado. Comprobar en todas las combinaciones ésta situación.

[ algoritmo ] [ diagrama flujo ]
..

---

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2014_T2 Triángulos aleatorios en rectángulo
# Propuesta de solución: edelros@espol.edu.ec

import numpy as np
import random as rnd
import matplotlib.pyplot as plt

# INGRESO
n = int(input(" cuántos triángulos: "))
maxa = int(input(" rango lado a: "))
maxb = int(input(" rango lado b: "))

# PROCEDIMIENTO
equilatero = 0
isosceles  = 0
escaleno   = 0
colineal   = 0

i = 1
while (i<=n):
    
    # puntos aleatorios
    x1 = int(rnd.random()*maxa) +0
    y1 = int(rnd.random()*maxb) +0
    
    x2 = int(rnd.random()*maxa) +0
    y2 = int(rnd.random()*maxb) +0

    x3 = int(rnd.random()*maxa) +0
    y3 = int(rnd.random()*maxb) +0

    # distancias entre puntos
    a = np.sqrt((x2-x1)**2 + (y2-y1)**2)
    b = np.sqrt((x3-x2)**2 + (y3-y2)**2)
    c = np.sqrt((x1-x3)**2 + (y1-y3)**2)

    # realiza la gráfica de cada triángulo
    plt.plot([x1, x2], [y1, y2])
    plt.plot([x2, x3], [y2, y3])
    plt.plot([x1, x3], [y1, y3])

    # clasifica triángulos
    s1 = a + b
    s2 = b + c
    s3 = c + a
    if (s1==c or s2==a or s3==b):
        colineal = colineal + 1
    else:
        if (a==b and b==c):
            equilatero = equilatero+1
        else:
            if (a!=b and b!=c and c!=a):
                escaleno = escaleno+1
            else:
                isosceles = isosceles+1
    i=i+1

# SALIDA
print("equilateros: ")
print(equilatero)
print("escalenos: ")
print(escaleno)
print("isosceles: ")
print(isosceles)
print("colineales: ")
print(colineal)

# muestra la gráfica
plt.show()

Resultado del algoritmo

 cuántos triángulos: 100
 rango lado a: 10
 rango lado b: 10
equilateros: 
0
escalenos: 
90
isosceles: 
4
colineales: 
6
>>>
 cuántos triángulos: 100
 rango lado a: 10
 rango lado b: 10
equilateros: 
0
escalenos: 
87
isosceles: 
6
colineales: 
7
>>> 

[ algoritmo ] [ diagrama flujo ]
..

---

Diagrama de Flujo

[ algoritmo ] [ diagrama flujo ]

---

ejercicios resueltos Python 1eva_iit2014_t2 pdf

Ejercicios: 1Eva_IIT2014_T1 Números amigos

[ algoritmo ] diagrama flujo: [ mientras-repita ] [ repita-hasta ]

Dos números enteros positivos a y b son amigos sí solo sí la suma de los divisores de a es igual al número b, y la suma de los divisores de b es igual al número a.

Se divide el ejercicio en dos partes, primero la suma de divisores del número a.

# suma de divisores para "a"
atotal = 1
i = 2
while (i<a):
      r = a%i
      if (r==0):
          atotal = atotal + i
      i = i + 1

El concepto se repite par la suma de divisores de b.

El resultado se obtiene comparando las sumas de divisores

if (atotal==b and btotal==a):
      namigos = 1
else:
      namigos = 0

Se muestran los resultados al final

[ algoritmo ] diagrama flujo: [ mientras-repita ] [ repita-hasta ]
..

---

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2014_T1 Números amigos
# Propuesta de solucion: edelros@espol.edu.ec

# INGRESO
a = int(input("número a: "))
b = int(input("número b: "))

# PROCEDIMIENTO

# suma de divisores para "a"
atotal = 1
i = 2
while (i<a):
      r = a%i
      if (r==0):
          atotal = atotal + i
      i = i + 1

# suma de divisores para "b"
btotal = 1
j = 2
while (j<b):
      r = b%j
      if (r==0):
          btotal = btotal + j
      j = j + 1

if (atotal==b and btotal==a):
      namigos = 1
else:
      namigos = 0

# SALIDA
print('números amigos: ', namigos)

resultado del algoritmo

número a: 220
número b: 284
números amigos:  1
>>> 
número a: 221
número b: 284
números amigos:  0

[ algoritmo ] diagrama flujo: [ mientras-repita ] [ repita-hasta ]
..

---

Diagrama de Flujo: Mientras-Repita

[ algoritmo ] diagrama flujo: [ mientras-repita ] [ repita-hasta ]
..

---

Diagrama de Flujo: Repita-Hasta

[ algoritmo ] diagrama flujo: [ mientras-repita ] [ repita-hasta ]

ejercicios resueltos Python 1eva_iit2014_t1 pdf

Ejercicio: 1Eva_IT2013_T4 Tabular atención al cliente

Para el ejercicio por simplicidad, en el bloque de ingreso se tabula también la "evaluación" del cliente para el servicio en un arreglo.

Recuerde repasar el algoritmo del mayor

---

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2013_T4 Tabular atención al cliente
# Tarea: literal c)
#  calcular promedio dentro de procedimiento
#  mostrar clientes con atencion menor al promedio en SALIDA
import numpy as np

# INGRESO
n = int(input('cuantos clientes: '))
atencion = np.zeros(n+1, dtype=int)
cuenta   = np.zeros(6, dtype=int) # de 0 a 5
cliente  = 1
while not(cliente>n):
    pregunta = 'CLIENTE '+str(cliente)+' evalue: '
    nota = int(input(pregunta))
    
    if (nota>=1 and nota<n):
        atencion[cliente] = nota
        cuenta[nota] = cuenta[nota] + 1
    cliente = cliente + 1

# Algoritmo Mayor
mayor = 1  
nota  = 2 
while not(nota>5):
    if (cuenta[nota]>cuenta[mayor]):
        mayor = nota
    nota = nota + 1
    
# SALIDA
print('las evaluaciones fueron: ')
print(cuenta)
print('mayor: ',mayor)
print('evaluacion [mayor]: ',cuenta[mayor])

resultado esperado:

cuantos clientes: 5
CLIENTE 1 evalue: 1
CLIENTE 2 evalue: 1
CLIENTE 3 evalue: 1
CLIENTE 4 evalue: 2
CLIENTE 5 evalue: 2
las evaluaciones fueron: 
[0 3 2 0 0 0]
mayor:  1
evaluacion [mayor]:  3
>>> 

Tarea: literal c,  calcular promedio y seleccionar clientes que presentaron evaluación menor al promedio

Ejercicio: 1Eva_IT2013_T1 Primos gemelos

Para facilitar el ejercicio, pues no se dispone de una lista de números primos, se inicia generando usa secuencia ordenada de números naturales a partir del 2 hasta el número n donde se desea realizar la observación.

# PROCEDIMIENTO
# intervalo de búsqueda de números primos
secuencia = np.arange(2,n+1,1)
tamano = len(secuencia)

# supone que todos son primos
cumple = np.ones(tamano, dtype=int)

Se simplifica el procedimiento de generar la secuencia usando la función de Numpy para generar un rango entre un intervalo [a,b) y dando el incremento: np.arange(a,b,incremento). Siendo un lado del intervalo no incluyente, pues se define con paréntesis, se añade el límite usando n+1.

Sobre la secuencia, se usa un algoritmo de búsqueda de números primos realizado en clase para obtener un vector que tenga solo números primos. Otro ejemplo como repaso, puede revisar el ejercicio de la Criba de Eratóstenes.

La búsqueda de primos gemelos consiste en comparar dos números consecutivo del vector soloprimos. Si la diferencia entre ellos es 2, se encontraron los números buscados. La respuesta se puede dar por medio de un nuevo vector o lista, o semejante al ejercicio de la Criba de Eratóstenes se puede usar un arreglo de banderas.

---

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2013_T1 Primos gemelos
import numpy as np

# INGRESO
n = int(input('límite n: '))

# PROCEDIMIENTO
# intervalo de búsqueda de números primos
secuencia = np.arange(2,n+1,1)
tamano = len(secuencia)

# supone que todos son primos
cumple = np.ones(tamano, dtype=int)

# revisa cada número de secuencia
posicion = 0
while (posicion<tamano):
    n = secuencia[posicion]
    
    # PROCEDIMIENTO esprimo 
    esprimo = 1
    divisor = 2
    while not(divisor>=n or esprimo==0):
        r = n%divisor
        if (r == 0):
            esprimo = 0
        divisor = divisor + 1
        
    cumple[posicion] = esprimo
    posicion = posicion + 1

cuantos = np.sum(cumple)
soloprimos = np.zeros(cuantos,dtype=int)

# separa solo los primos
posicion = 0
i = 0
while not(posicion>=tamano):
    if (cumple[posicion]==1):
        soloprimos[i] = secuencia[posicion]
        i = i + 1
    posicion = posicion + 1

# SALIDA

# BUSCA GEMELOS
i = 0
while not(i>=(cuantos-1)):
    sigue = i + 1
    diferencia = soloprimos[sigue] - soloprimos[i]
    if (diferencia==2):
        print('pareja gemelo: ')
        print(soloprimos[i],soloprimos[sigue])
    i = i + 1
    
# revisando resultados
print('secuencia: ', secuencia)
print('cumple:    ', cumple)
print('soloprimos:', soloprimos)

resultado del algoritmo

pareja gemelo: 
3 5
pareja gemelo: 
5 7
secuencia  [2 3 4 5 6 7 8 9]
cumple:    [1 1 0 1 0 1 0 0]
soloprimos: [2 3 5 7]
>>> 

Ejercicios: 1Eva_IIT2013_T3 Juego Semillero

Propuesta de solución en Python, realizada solo para dos jugadores.

Observe que al lanzar dos dados, el intervalo de valores posibles es [2,12].

dado1 = int(rnd.random()*6)+1
dado2 = int(rnd.random()*6)+1
suma  = dado1 + dado2

La variable quien determina el turno del jugador.

Se lanzan los dados como números aleatorios, se acumula los puntos para cada jugador y se resta la cantidad de fichas del semillero.

if (suma<=semillero):
    A = A + suma
    semillero = semillero -suma
else:
    A = A +semillero
    semillero = 0

Se cambia el turno del jugador y se repite el proceso.

    # cambia jugador
    if (quien==1):
        quien = 2
    else:
        quien = 1

TAREA: Implementar con arreglos para n jugadores.

---

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2013_T3 Juego Semillero
# usando solo dos jugadores
import random as rnd

# INGRESO
apuesta = int(input('cuantas canicas: '))
while not(apuesta>=20):
    apuesta = int(input('mas de 20 canicas: '))

# PROCEDIMIENTO
semillero = 2*apuesta
A = 0
B = 0
quien = 1
while not(semillero<=0):

    # Juega A
    if (quien==1):
        dado1 = int(rnd.random()*6)+1
        dado2 = int(rnd.random()*6)+1
        suma  = dado1 + dado2
        if (suma<=semillero):
            A = A + suma
            semillero = semillero -suma
        else:
            A = A +semillero
            semillero = 0

    # Juega B
    if (quien==2):
        suma = int(rnd.random()*11)+2
        if (suma<=semillero):
            B = B + suma
            semillero = semillero - suma
        else:
            B = B + semillero
            semillero = 0
            
    # cambia jugador
    if (quien==1):
        quien = 2
    else:
        quien = 1

# Determina ganador
gana = 1
if (A < B):
    gana = 2
if (B==A):
    gana = 0
    
# SALIDA
print('canicas de A: ', A)
print('canicas de B: ', B)
print('estado semillero: ', semillero)
print('jugador ganador: ', gana)

Ejecución del algoritmo

cuantas canicas: 20
canicas de A:  25
canicas de B:  15
estado semillero:  0
jugador ganador:  1
>>> 
cuantas canicas: 20
canicas de A:  20
canicas de B:  20
estado semillero:  0
jugador ganador:  0
>>> 
cuantas canicas: 20
canicas de A:  22
canicas de B:  18
estado semillero:  0
jugador ganador:  1
>>> 

Ejercicios: 1Eva_IIT2013_T2 Números palíndromo con Python

Literal a. Para invertir los dígitos de un número, se usan residuo y el cociente para extraer cada dígito y rearmarlo en otro número con posiciones invertidas.

Sec compara el número de forma inversa para verificar si el igual al número original, siendo solamente así un número palíndromo.

Tarea: implementar el literal b a partir de la solución del literal a.

Para iniciar la búsqueda de los números palíndromos se inicia con dos dígitos es decir numero=10. Se aplica el algoritmo al número y se repite el proceso con un lazo hasta llegar al millón-1

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2013_T2 Números palíndromo

# INGRESO
numero = int(input('numero a revisar: '))

# PROCEDIMIENTO
numcopia = numero
cociente = numero

# invierte dígitos del número
invertido = 0
while not(cociente<=0):
    numcopia = cociente
    cociente = numcopia//10
    residuo  = numcopia%10
    invertido = invertido*10 + residuo

# revisa si el número es igual a invertido
if (invertido == numero):
    palindromo = 1
else:
    palindromo = 0

# SALIDA
print('numero invertido: ', invertido)
print('Palindromo:', palindromo)

Ejecución del algoritmo

numero a revisar: 1991
numero invertido:  1991
Palindromo: 1
>>> 
numero a revisar: 2112
numero invertido:  2112
Palindromo: 1
>>> 
numero a revisar: 2020
numero invertido:  202
Palindromo: 0
>>>