Categoría: Unidades

Unidades de Estudio

4.2 Matrices en programación - Arreglos de dos dimensiones en Python
Arreglos: [ índice ][ Vector ] [ Matriz ] || [ cadenas/string ] [listas]

Las matrices en programación se manejan como arreglos de Numpy.
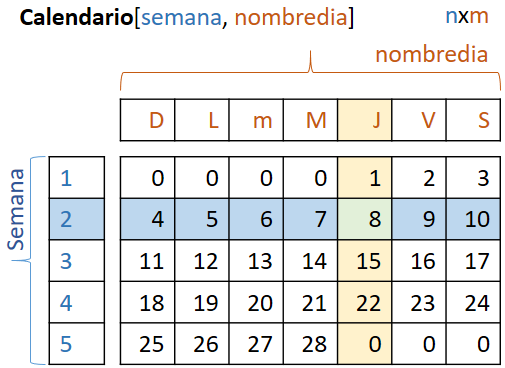
La interpretación de los datos de una Matriz o arreglo puede ser desde un sistema de ecuaciones, una tabla de goles de un campeonato o una hoja de calendario.

Al igual que los vectores, las matrices en arreglos tienen como componentes: "nombre", "índice" y "tamaño". Los valores de tamaño dependen de las dimensiones de la matriz. Para los primeros ejercicios serán rectangulares de nxm.

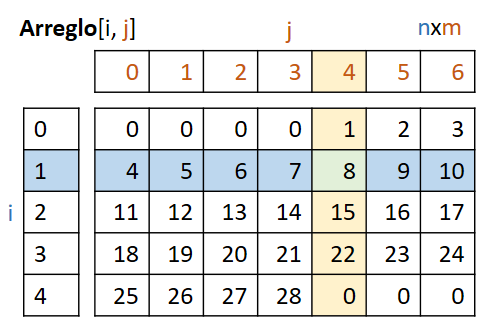
Los índices a diferencia de el álgebra, inician en cero.

En los ejercicios, la matriz de dos dimensiones usa como índices de filas la variable "i" y para columnas "j".

Arreglos: [ índice ][ Vector ] [ Matriz ] || [ cadenas/string ] [listas]

Matrices en programación con Numpy-Python

Para un mejor manejo de matrices en programación, se usan las funciones de la librería Numpy (Numerical Python) que se incorporan en el bloque de inicio con el alias np.
```
import numpy as np
```
Definir una matriz de nxm, con ceros o llena de unos, requiere la instrucción:
```
>>> 
import numpy as np
>>> n = 5
>>> m = 7
>>> matriz0 = np.zeros(shape=(n,m), dtype=float)
>>> matriz0
array([[0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0.]])
>>> matriz1 = np.ones(shape=(n,m), dtype=float)
>>> matriz1
array([[1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1.]])
>>> 
```
El tipo de matriz (dtype=int) se añade para indicar que la matriz tiene datos tipo entero, la forma predeterminada para los datos es tipo real (dtype=float)

Las dimensiones de la matriz se obtienen mediante la instrucción con Numpy:
```
>>> np.shape(matriz0)
(5, 7)
>>> tamano = np.shape(matriz0)
>>> tamano
(5, 7)
>>> tamano[0]
5
>>> tamano[1]
7
>>> dimension = np.ndim(matriz0)
>>> dimension
2
>>> 
```
entre otras operaciones en Numpy que reflejan las operaciones de matrices de álgebra.

Referencias: Inicie con la definición de matrices del álgebra lineal:

https://blog.espol.edu.ec/matg1049/cl1-02-sistema-de-ecuaciones-lineales/

Las operaciones básicas de matrices se describen también en álgebra lineal:

https://blog.espol.edu.ec/matg1049/cl2-07-operaciones-entre-subespacios/

Algoritmos sobre Matrices en Análisis y Métodos Numéricos

La Unidad 3 Sistemas de Ecuaciones del curso Análisis Numérico desarrolla los algoritmos en Python en base a los métodos matemáticos.

3.2 Pivoteo parcial por filas con Python

3.3 Método de Gauss con Python

Interpretación de matrices

Observe el siguiente video y plantee la relación con el tema de arreglos, matrices, dimensiones y computación.

Las aplicaciones de las matrices | Lo que desearía que mis maestros me hubieran dicho antes. Zach Star. 11 oct 2019.

Arreglos: [ índice ][ Vector ] [ Matriz ] || [ cadenas/string ] [listas]
2015-06-05
4.1.1 Vectores como arreglos en programación Arreglos - Ejercicios resueltos en Python
Tarea

Ejemplo Fibonacci

Ejemplo Primos

Ejemplos

1. Tarea

1Eva2005TI_T3 Arreglo aleatorio binario a decimal

1Eva2001TI_T6 Piloto y copiloto para nave

1Eva2002TII_T3 Conjetura de Ullman

1Eva2008TII_T4 Área del polígono convexo por triángulos

2. Ejemplo 1 - Secuencia de Fibonacci

Referencia: Bucle o Ciclos Tarea Ejercicio 12

La secuencia de Fibonacci es muy reconocida en la matemática. Como introducción al tema se recomienda observar el video de "misterio de las matemáticas" que tiene una explicación interesante entre los tiempos 2:33 y 6:40, por lo que el video inicia en el minuto 2:33.

La secuencia se desarrolla a partir de dos números: 1 y 1

El siguiente término se obtiene sumando los dos anteriores:
```
1 1 2 3 5 8 13 21 ...
a+b=c
  a+b=c
    a+b=c
```
El algoritmo primero se presenta en el diagrama de flujo para facilidad visual de los pasos.

Al requerir mostrar toda la secuencia, en lugar de un solo valor, aparece la necesidad de usar un vector.

Para éste caso usamos la librería Numpy para obtener los siguientes resultados:
```
¿cuál término?: 8
término n-ésimo:  21
secuencia:  [ 1  1  2  3  5  8 13 21]
>>> 
```
Algoritmo en Python

Se modifican las instrucciones para añadir la secuencia en un vector:
```
# secuencia de Fibonacci
# usando vectores
import numpy as np

# INGRESO
nesimo = int(input('¿cuál término?: '))

# PROCEDIMIENTO
a = 1
b = 1
terminos = 2
secuencia = np.zeros(nesimo,dtype = int)
secuencia[0] = 1
secuencia[1] = 1

while not(terminos>=nesimo):
    c = a+b
    secuencia[terminos] = c
    terminos = terminos+1
    a = b
    b = c
    
# SALIDA
print('término n-ésimo: ',c)
print('secuencia: ', secuencia)
```
Tarea

Ejemplo Fibonacci

Ejemplo Primos

Ejemplos

3. Ejemplo 2 - números primos

Referencia: 1Eva2015TII_T3 Vector de números primos

Primero desarrolle el algoritmo para un número cualquiera "n".

Como hipótesis, inicie considerando que el número es primo, esprimo=1, luego pruebe con cada uno de los divisores en el intervalo entre 2 y (n-1).

La divisibilidad se revisa con el residuo entre el número n y los divisores del intervalo [2,n-1].

Primero con divisor=2. El número 1 no cuenta pues todos los números son divisibles para 1.

Si el residuo calculado tuvo resultado cero, el número n no es primo, esprimo=0. Continua las pruebas con el siguiente divisor, divisor = divisor +1

Se revisa si se han probado con todos los números inferiores a n o que el resultado ya no es primo, esprimo=0.

Se muestran los resultados.

El esquema del ejemplo se muestra en el diagrama de flujo.

Algoritmo en Python

Convirtiendo las instrucciones de diagrama de flujo a instrucciones en Python:
```
# 1ra Evaluación II Término 2015. Tema 3
# numeros primos

# INGRESO
n = int(input('primo a revisar: '))

# PROCEDIMIENTO ES PRIMO
esprimo = 1

divisor = 2
while not(divisor>=(n-1) or esprimo==0):
    residuo = n%divisor
    if (residuo==0):
        esprimo=0
    divisor = divisor+1

# SALIDA
print('numero primo: ', esprimo)
```
Tarea

En una secuencia de números enteros, identifique cuales son números primos.

Reutilice el algoritmo anterior para almacenar cada resultado en un vector, indicando 1 si es primo y 0 si no lo es.

Luego de probar que el algoritmo funciona, realice un bloque de ingreso para la secuencia de prueba.
```
numeros prueba:  [ 2  3  4  5  6  7  8  9 10]
cumple esprimo:  [ 1  1  0  1  0  1  0  0  0]
>>> 
```
```
# 1ra Evaluación II Término 2015
# numeros primos
import numpy as np

# INGRESO
probar = np.array([2,3,4,5,6,7,8,9,10])

# PROCEDIMIENTO
tamano = len(probar)
cumple = np.ones(tamano, dtype=int)
posicion =  0
while not(posicion==tamano):
    n = probar[posicion]
    
    # PROCEDIMIENTO ES PRIMO
    esprimo = 1
    i = 2
    while not(i>=(n-1) or esprimo==0):
        r = n%i
        if (r==0):
            esprimo=0
        i = i+1
    
    cumple[posicion] = esprimo
    posicion = posicion+1

# SALIDA
print('numeros prueba: ', probar)
print('cumple esprimo: ', cumple)
```
Tarea

Ejemplo Fibonacci

Ejemplo Primos

Ejemplos

4. Ejemplos - Ejercicios resueltos de vectores

Vectores - Arreglos unidimensionales con Python y Numpy

1Eva2013TI_T4 Tabular atención al cliente

solución propuesta: s1Eva_IT2013_T4 Tabular atención al cliente

1Eva2002TII_T2 Color de placas de vehículos

solución propuesta: s1Eva2002TII_T2 Color de placas de vehículos

1Eva2008TI_T2 Criba de Eratóstenes

solución propuesta: s1Eva2008TI_T2 Criba de Eratóstenes

Arreglos unidimensionales y números aleatorios

1Eva2008TI_T3 Simular precio de petroleo

Solución literal c: s1Eva2008TI_T3 Simular precio de petroleo

1Eva2010TII_T3 Juego del amigo secreto

Solución propuesta: s1Eva2010TII_T3 Juego del amigo secreto

1Eva2007TII_T2 Juego de la Ruleta

Solución propuesta: s1Eva2007TII_T2 Juego de la Ruleta

Arreglos, acumuladores y contadores

1Eva2010TII_T1 Censo de instrucción por género

Solución propuesta: s1Eva2010TII_T1 Censo de instrucción por género

1Eva2011TI_T3 Calcular ventas por región

Solución propuesta: s1Eva2011TI_T3 Calcular ventas por región

1Eva2013TI_T1 Primos gemelos

Solución propuesta: s1Eva2013TI_T1 Primos gemelos

1Eva2008TI_T2 Criba de Eratóstenes

Solución propuesta: s1Eva2008TI_T2 Criba de Eratóstenes

Tarea

Ejemplo Fibonacci

Ejemplo Primos

Ejemplos
2015-06-03
4.1 Vectores en programación - Arreglos de una dimensión en Python
Algoritmo

Arreglos

Ingreso

índices

Procedimiento

Salida

Al disponer de varios de datos de igual tipo y relacionados se manejan como un conjunto. Ejemplo: una lista de calificaciones de una lección o las edades de los estudiantes.

estudiante edad[estudiante]
1 17
2 21
3 19

El conjunto de datos se maneja como un “arreglo” que tiene las siguientes características:
- Todos los datos son de igual tipo (enteros, reales, lógicos, etc.)
- Se conoce su “tamaño”, es decir la cantidad de elementos en el arreglo.
- El arreglo se identifica por medio del nombre del conjunto ordenado de datos.
- Cada elemento se identifica por una variable índice que da su posición.
edad = \begin{pmatrix} 17\\21\\19 \end{pmatrix}
En éste ejemplo se puede observar que:
- todos los datos de las edades son tipo entero, int
- el tamaño o cantidad de estudiantes es n=3 en el arreglo
- los datos corresponden a la “edad”, nombre del arreglo
- mediante su posición en la lista i, se identifica al estudiante. El estudiante 2, i=2, la edad es edad[2]=21.
Otro ejemplo , temperaturas por día. Los datos son tipo Real, float:

día 1 2 3 4
temperatura[día] 28.6 24.9 26.5 25.1

Tamaño n=4, temperatura[2]=24.9

Para éste caso, el arreglo contiene las mediciones de temperatura en varios días, para éste caso es de 4 días, por lo que el arreglo es de tamaño 4. Todos los datos son números reales, si se quiere conocer la temperatura de un día específico se usa la variable índice día, con lo que se obtiene el valor de 24.9.

Algoritmo

Arreglos

Ingreso

índices

Procedimiento

Salida

Arreglos en algoritmos

Los arreglos en algoritmos se manejan como vectores y matrices en álgebra. Python dispone de la librería Numpy para manejo de arreglos, por lo que en el bloque de inicio se requiere pedir la librería "numpy" con el álias "np".
```
import numpy as np
```
En el caso que se usen arreglos, los bloques de ingreso deben reflejar las acciones para llenar los datos.

Bloque de Ingreso

La primera pregunta para llenar una lista de temperaturas es para conocer cuántos datos se encuentran registrados. Por lo que primero se preguntará el tamaño n del arreglo .

El ingreso de datos es de forma ordenada, por lo que se inicia el índice para solicitar el valor del primero de la lista. Por ejemplo:
día=1,

Luego se solicita el ingreso de la temperatura de cada día: temperatura[día] .

Se continúa el siguiente índice , sumándole uno, para repetir la operación hasta completar el ingreso de todos los datos.

Se repite el procedimiento para cada elemento del arreglo "temperatura".

Algoritmo

Arreglos

Ingreso

índices

Procedimiento

Salida

Indices en arreglos

Los índices en arreglos se manejan de forma semejante a un vector en álgebra. Sin embargo, la numeración de casillas empieza en cero.

i 0 1 2 3
día 1 2 3 4
temperatura[día] 28.6 24.9 26.5 25.1

Por lo que el día 2, tiene índice 1. El índice está en el arreglo desplazado en una posición.
```
import numpy as np
temperatura = np.array([28.6, 24.9, 26.5, 25.1])

>>> temperatura[2]
26.5
>>> temperatura[1]
24.9
>>> 
>>> len(temperatura)
4
>>> 
```
Asunto para recordar cuando se realicen las operaciones en el arreglo.

Algoritmo

Arreglos

Ingreso

índices

Procedimiento

Salida

Bloque de procedimiento

Al manejar el conjunto de datos ordenado se puede realizar los cálculos individualmente sobre cada elemento. O se puede manejar el conjunto con las reglas de vectores o matrices.

Por ejemplo, promediar la temperaturas, requiere sumar todas las temperaturas y dividirlas para la cantidad de datos (tamaño)
```
# PROCEDIMIENTO
promedio = np.sum(temperatura)/n
```
Algoritmo

Arreglos

Ingreso

índices

Procedimiento

Salida

Bloque de Salida

Para la presentación de datos, cuando se dicta o se muestra uno por uno, se procede de forma semejante al bloque de ingreso.

En algunos lenguajes estructurados, existen formas de presentar todo el conjunto mediante una sola instrucción.
```
# temperaturas promedio
import numpy as np

# INGRESO
n = int(input('cuántos días: '))

temperatura = np.zeros(n,dtype=float)
dia = 0
while not(dia>=n):
    temperatura[dia] = float(input('t: '))
    dia = dia + 1

# PROCEDIMIENTO
promedio = np.sum(temperatura)/n

# SALIDA
print('promedio t: ',promedio)
print(temperatura)
```
que al ejecutar el algoritmo obtenemos
```
cuántos días: 4
t: 28.6
t: 24.9
t: 26.5
t: 25.1
promedio t:  26.275
[28.6 24.9 26.5 25.1]
>>> 
```
Algoritmo

Arreglos

Ingreso

índices

Procedimiento

Salida
2015-06-02
Unidad 04 Arreglos, Listas y Cadenas de caracteres

4.1 Vectores en programación - Arreglos de una dimensión

4.2 Matrices en programación - Arreglos de dos dimensiones

4.2.1 Matrices en programación, Arreglos - Archivo Abrir/Guardar con Numpy

4.3 Cadenas de caracteres/strings - vector de letras en Python

4.4 Listas como conjuntos en Python

2015-06-01
3.5.3 Bases Numéricas en programación - Ejercicios resueltos y Tarea

Bases numéricas se usan para diferentes propósitos, para interpretarlas apropiadamente se requieren algoritmos que usan cocientes, residuos y acumuladores.

Se presentan algunos ejercicios resueltos en los que se requiere realizar el cambio de bases numérica desarrollados con Python.

Sistemas de Numeración - Bases Numéricas

Ejemplos: ejercicios resueltos con bases numéricas

1Eva_IIT2008_T1 Odómetro OCTAL

Solución propuesta: s1Eva_IIT2008_T1 Odómetro OCTAL

1Eva_IIT2003_T1 Cambiar Decimal a Octal

Solución propuesta: s1Eva_IIT2003_T1 Cambiar Decimal a Octal

1Eva_IT2005_T3 Arreglo aleatorio binario a decimal

Solución propuesta: s1Eva_IT2005_T3 Arreglo aleatorio binario a decimal

Actividades independientes

Otros ejercicios que para practicar lazos/bucles, acumuladores, cocientes y residuos.

1Eva_IIT2002_T3 Conjetura de Ullman

1Eva_IIT2008_T4 Área del polígono convexo por triángulos

1Eva_IT2001_T6 Piloto y copiloto para nave

2015-05-28
3.5.2 Número Decimal a Binario - Algoritmo Básico en Python
[ Decimal a Binario ] [ Ejercicio ] [ Algoritmo ] || [ Binario a Decimal ]

..

1. Número Decimal a Binario

Los números decimales se convierten a base binaria para mostrarlos por ejemplo en códigos de barra.

La base numérica binaria es ampliamente usada en informática o computación.

[ Decimal a Binario ] [ Ejercicio ] [ Algoritmo ] || [ Binario a Decimal ]

..

2. Ejercicio: Cinco en binario

Para convertir el número Decimal 5 en Binario hay que descomponer el número en la nueva base numérica, para luego trabajar con los residuos y ubicar cada uno desde la posición menos significativa a la más significativa.

Las operaciones se basan principalmente en el uso de cocientes, residuos y acumuladores y el proceso se muestra en la figura:

Observe la diferencia en las operaciones para el divisor y la base, las operaciones son similares a las del ejercicio de Binario a Decimal.

Cambia el divisor y la ponderación usadas, sin embargo las operaciones seguirán siendo básicamente las mismas.

Con esta observación se pueden plantear los cambios de base con otras bases numéricas, por ejemplo la de base 8 también conocida como Octal.
[ Decimal a Binario ] [ Ejercicio ] [ Algoritmo ] || [ Binario a Decimal ]
..

3. Algoritmo Decimal a Binario

Puesto que el ejercicio es una variante del mostrado como Binario a Decimal, se muestra directamente su forma en: Diagrama de flujo, pseudo-código y en Python.

El ejemplo en seudo-código:
```
Proceso DecimalBinario
	Leer decimal
	binario ← 0
	i ← 0
	Mientras decimal > 0
		digito ← decimal mod 2
		decimal ← trunc(decimal/2)
		binario ← binario+digito*10^i
		i ← i + 1
	FinMientras
	Escribir binario
FinProceso
```
Algoritmo en Python
```
# Decimal a binario

# INGRESO
decimal = int(input("número decimal: "))

# PROCEDIMIENTO
binario = 0
i = 0
while (decimal>0):
    digito  = decimal%2
    decimal = int(decimal//2)
    binario = binario+digito*(10**i)
    i = i+1
# SALIDA
print("en binario: ",binario)
```
Resultados en Python
```
número decimal:5
en binario:  101
>>>
```
Ejercicios:
1. Realizar los algoritmos Binario a Decimal y Decimal a Binario usando el lazo Repita-Hasta.
2. Crear un algoritmo para convertir un número de base numérica x a base y.
  Comprobar el algoritmo usando los valores: 23_x número_y.
  Sugerencia, convierta el número de la base x primero a decimal y luego transforme el resultado a la siguiente base numérica y.
[ Decimal a Binario ] [ Ejercicio ] [ Algoritmo ] || [ Binario a Decimal ]

Referencia: Cadenas de Supermercados - Gigantes de la comida. History Latinoamérica. 18 Julio 2025. minuto 8:15 códigos de barra.
2015-05-27
3.5.1 Número Binario a Decimal - Algoritmo Básico en Python
[ Binario a Decimal ] [ Ejercicio ] [ Algoritmo ] || [ Decimal a Binario ]
..

1. Binario a Decimal

Referencia: Baldor, Aurelio (1974). Capítulo III Otros sistemas de numeración. Aritmética de Baldor, Guatemala. Cultural Centroamericana S.A..https://es.wikipedia.org/wiki/Sistema_binario

Los números binarios se conforman con los símbolos 0 y 1, que se combinan para representar cualquier número.
Una etiqueta de un producto en código de barras es la representación binaria del número que identifica el producto.

Para representar números superiores a 1 dígito, se aplica un método semejante al de formación de números decimales, combinando ordenadamente los símbolos. Se repiten las combinaciones de dígitos anteriores y se le añade un dígito para continuar la numeración

Decimal Binaria

0 0

1 1

2 10

3 11

4 100

5 101

6 110

7 111

8 1000

9 1001

10 1010

11 1011

12 1100

… …

En el sistema binario se utiliza la ponderación por posición de dígito en la misma forma que en la numeración decimal, por ejemplo:

posición 3 2 1 0

ponderación 2³ 2² 2¹ 2⁰

peso en decimal 8 4 2 1

Número en binario 5₍₁₀₎=101₍₂₎
=0*8+1*4+0*2+1*1 0 1 0 1
- La posición más a la derecha es menos significativa y de menor ponderación o peso: 2⁰
- La siguiente posición hacia la izquierda tiene un peso equivalente a: 2¹
- La siguiente posición a la izquierda usa un equivalente a: 2³
- Y así sucesivamente.
Se puede encontrar el valor decimal de un número binario cualquiera multiplicando el dígito correspondiente por el “peso” que tiene y sumando los resultados parciales.

[ Binario a Decimal ] [ Ejercicio ] [ Algoritmo ] || [ Decimal a Binario ]

..

2. Ejercicio: Convertir a decimal el binario 101

Para convertir el número binario 101 a decimal, se realizan las operaciones de ponderación usando los residuos de la división para 10 del número en base 10.

La operación de residuo es la extracción de cada dígito empezando por el menos significativo. cada dígito se pondera por 2ⁱ, siendo i la posición del dígito.

[ Binario a Decimal ] [ Ejercicio ] [ Algoritmo ] || [ Decimal a Binario ]

..

3. Algoritmo de Binario a Decimal

Para realizar el algoritmo, se separa cada dígito del número binario, y luego se realiza la operación de ponderación para acumularla en el resultado final.

En la ponderación se usará un contador de posición para ser usado como el exponente de la base 2.

El algoritmo en diagrama de flujo se representará como:

Algoritmo en Python
```
# Binario a Decimal

binario = int(input("número en binario: "))

decimal = 0
i = 0
while (binario>0):
    digito  = binario%10
    binario = int(binario//10)
    decimal = decimal+digito*(2**i)
    i = i+1
# SALIDA
print("en decimal: ",decimal)
```
con los siguientes resultados:
```
>>> 
número en binario: 101
en decimal:  5
>>> 
número en binario: 1000
en decimal:  8
>>> 
número en binario: 111
en decimal:  7
>>> 
```
[ Binario a Decimal ] [ Ejercicio ] [ Algoritmo ] || [ Decimal a Binario ]

Referencia: Cadenas de Supermercados - Gigantes de la comida. History Latinoamérica. 18 Julio 2025. minuto 8:15 códigos de barra.
2015-05-26
3.5 Bases Numéricas en programación - Introducción

Referencia: Van Rossum 15 p105, Rodriguez 5.6.5 p63, Sistemas de numeración

A través del tiempo la humanidad adoptado diferentes formas de numeración, tanto en símbolos como en bases.

Las formas simbólicas de numeración más conocidas son:
la arábiga (0, 1, 2, 3,… 9) usada en estos días, y
la romana (I, II, III, IV, V, VI,…X,…).

El uso de computadores nos obliga a revisar el tema de sistemas de numeración, debido a que internamente el computador opera en numeración binaria basada en dos símbolos representados como 0 y 1.

La electrónica digital, que permite construir una computadora, trabaja sobre dos estados del circuito: abierto o cerrado, verdadero o falso, 1 o 0.

Es común ver en las etiquetas de un producto el denominado código de barras que facilita el trabajo de identificar el producto vendido.

El código de barras permite usar un dispositivo para “leer” la representación binaria del producto, cada barra de color blanco o negro representa un dígito binario del número. Para estos casos es necesario disponer de un algoritmo que permita leer y convertir un código de producto de binario a decimal, así como el decimal a binario en el caso de la impresión o escritura del código de barras.

Base Numérica Decimal

La base numérica 10 nos resulta muy natural y no requiere mucha descripción. Se basa en diez símbolos conocidos como numeración arábiga: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Para números superiores a 9 se añade a la izquierda un dígito y se los combina ordenadamente: 10, 11, 12, …, 19, 20, 21, …

Al aplicar el mismo método de formación de números usando otra base numérica se obtiene resultados simulares como se muestra en la siguiente sección.

Referencias: Capítulo II Numeración. Baldor, Aurelio (1974). Aritmética de Baldor, Guatemala. Cultural Centroamericana S.A.

posición 3 2 1 0

ponderación 10³ 10² 10¹ 10⁰

peso en decimal 1000 100 10 1

numero decimal (1492) 1 4 9 2

2015-05-25
3.4.1 Números Aleatorios - Ejercicios resueltos en Python

Ejercicios resueltos sobre números aleatorios con simulaciones de juegos de mesa o aleatorios son una herramienta para encontrar una solución a una situación.

Ejercicios resueltos con Números Aleatorios, random()

1Eva_IIT2005_T4 Juego escaleras y serpientes

Solución propuesta: s1Eva_IIT2005_T4 Juego escaleras y serpientes,

1Eva_IIT2007_T1 Hormiga busca arroz

Solución Propuesta: s1Eva_IIT2007_T1 Hormiga busca arroz,

1Eva_IIT2012_T3 Hundir el barco enemigo

Solución propuesta: s1Eva_IIT2012_T3 Hundir el barco enemigo

1Eva_IIT2003_T4 Juego con icosaedros

Solución propuesta: s1Eva_IIT2003_T4 Juego con icosaedros

Ejercicios resueltos de Algoritmos con aleatorios,

Tipos de datos y variables numéricas (entero, real)

1Eva_IT2007_T1 Tiro al blanco con dardos

Solución propuesta: s1Eva_IT2007_T1 Tiro al blanco con dardos

1Eva_IIT2004_T3 Estimar π por Montecarlo

Solucion propuesta: s1Eva_IIT2004_T3 Estimar π por Montecarlo

1Eva_IT2008_T3 Simular precio de petroleo

Solución propuesta: s1Eva_IT2008_T3 Simular precio de petroleo

1Eva_IT2012_T2 Juego de carreras con dados

Solución propuesta: s1Eva_IT2012_T2 Juego de carreras con dados

Actividades independientes con números aleatorios

Se proponen algunos ejercicios para desarrollo a partir de lo practicado hasta esta sección.

1Eva_IT2004_T1 Aleatorios en región sombreada

3Eva_IT2003_T5 Calcular área de f(x) por Montecarlo

1Eva_IIT2004_T2 Apuestas a números con dados

1Eva_IT2007_T2 Convertir decimal a hexadecimal

2015-05-24
3.4 Números Aleatorios, al Azar o random con Python
Referencia: Van Rossum 10.6 p85, Rodríguez 5.9 p99, Downey 12.1

Para simular un número de azar se recurre al concepto de números aleatorios, que por ejemplo es el valor obtenido al lanzar un dado para juegos de tablero. Si el dado es estándar, no se puede predecir el valor que saldrá en el dado.

Un número aleatorio se define como un número real cualquiera en el intervalo [0,1).

La forma básica de generar un número aleatorio en Python es usando la librería random(), que se puede usar con operaciones adicionales para simulaciones de dados, movimientos en juegos, etc.
```
>>> import random as rnd
>>> rnd.random()
0.28033599517631624
>>> rnd.random()
0.07239272147532794
>>> 
```
Ejemplo de número aleatorios para un dado en Python

Para simular un dado de seis caras, que es un número aleatorio entero en el intervalo [0,6] se construye paso a paso:

dado ← entero(aleatorio*6)+1

1. Un número aleatorio

Se empieza con la forma básica para generar un número aleatorio entre [0,1)
```
>>> import random as rnd
>>> aleatorio = rnd.random()
>>> aleatorio
0.9531257439341784
```
2. Se debe convertir del intervalo [0,1) al intervalo de un dado de 6 caras,

multiplicando el aleatorio por 6, obteniendo un real de [0,6). No se incluye el 6.
```
>>> dado = aleatorio*6
>>> dado
5.7187544636050704
```
3. Sin embargo, el aleatorio de un dado es un número entero

Se extrae solo la parte entera para obtener un número entero [0,5]
```
>>> dado = int(aleatorio*6)
>>> dado
5
```
4. Para que el resultado sea [1,6],

se desplaza el intervalo a la derecha sumándole 1, con lo que el valor mínimo es 1 y el máximo será 6
```
>>> dado = int(aleatorio*6)+1
>>> dado
6
```
La fórmula final del ejemplo usada varias veces, mostrará que se obtiene un número diferente semejante a lanzar un dado de seis caras.
```
>>> dado = int(rnd.random()*6)+1
>>> dado
1
>>> dado = int(rnd.random()*6)+1
>>> dado
3
>>> 
```
Referencia: Elementos esenciales para programación: Algoritmos y Estructuras de Datos Latin Project. Primera Edición 2014. Sección 4.42. p.86

Ejercicio 1

1Eva_IT2008_T3 Simular precio de petroleo

Realice un algoritmo para simular el precio del barril de petróleo durante un mes de 30 días, suponiendo que son valores enteros que fluctúan en forma aleatoria entre $ 130 y $ 150 y se obtenga las siguientes respuestas:

a) El promedio del precio del petróleo.
b) ¿Cuál fue el día en el que estuvo más barato el barril de petróleo?

Diagrama de Flujo ejercicio - números aleatorios

Desarrollo

Para iniciar el algoritmo, se puede considerar como variable de entrada los días del mes, o asignarles directamente 30 días.

La primera aproximación al problema para responder el literal a) consiste en generar números aleatorios en el rango [130, 150] y acumular sus valores para el promedio.

Será necesario disponer de un contador para controlar el número de veces que se generan los precios de forma aleatoria en el lazo de repetición.

Una de las formas de resolver el problema es con un lazo repita hasta, cuyo diagrama de flujo se muestra a continuación:

Instrucciones en Python
```
# Ejercicio 1. Precio del petroleo
import random as rnd

# INGRESO
diasmes = int(input('dias que tiene el mes: '))

# PROCEDIMIENTO
total = 0
dia   = 0
rango = (150-130)+1
while not(dia>=diasmes):
    precio = int(rnd.random()*rango) + 130
    total  = total + precio
    dia    = dia + 1
promedio = total/diasmes

# SALIDA
print(promedio)
```
```
dias que tiene el mes: 30
137.56666666666666
>>> 
```
Para la pregunta b) es necesario analizar la manera de encontrar el día con el precio más barato.

En este caso se utilizará el algoritmo para búsqueda del menor, que consiste en iniciar con el supuesto para el valor menor de precio y día, probando contra el precio de cada día y de ser necesario se cambian los valores menores.

Diagrama de Flujo ejercicio - búsqueda de menor valor

Es un similar al caso de usar una hipótesis y realizar luego las pruebas.

Como supuesto, se escogerá el valor máximo de precio con el objetivo que el primer precio que aparece sustituye los valores.
```
# Ejercicio 1. Precio del petroleo
import random as rnd

# INGRESO
diasmes =  int(input('dias que tiene el mes: '))

# PROCEDIMIENTO
total = 0
dia = 0
rango = (150-130)+1
diamenor = 0
preciomenor = 150
while not(dia>=diasmes):
    precio = int(rnd.random()*rango) + 130
    total = total + precio
    if (precio<preciomenor):
        diamenor = dia
        preciomenor = precio
    dia = dia + 1
promedio = total/diasmes

# SALIDA
print(promedio)
print(diamenor)
```
```
dias que tiene el mes: 30
 140.06666666666666
 22
 >>>
```
Otra forma de realizar el algoritmo consiste en cambiar la perspectiva del lazo repita- hasta por un mientras repita. Para el cambio será necesario solo negar la expresión usada en el lazo repita-hasta en días<diasmes.

Diagrama de Flujo ejercicio - aleatorios y búsqueda de menor valor con mientras-repita
2015-05-23

Decimal	Binaria
`0`	`0`
`1`	`1`
`2`	`10`
`3`	`11`
`4`	`100`
`5`	`101`
`6`	`110`
`7`	`111`
`8`	`1000`
`9`	`1001`
`10`	`1010`
`11`	`1011`
`12`	`1100`
…	…

posición	3	2	1	0
ponderación	2³	2²	2¹	2⁰
peso en decimal	8	4	2	1
Número en binario 5₍₁₀₎=101₍₂₎ =08+14+02+11	0	1	0	1

posición	3	2	1	0
ponderación	10³	10²	10¹	10⁰
peso en decimal	1000	100	10	1
numero decimal (1492)	1	4	9	2

estudiante	edad[estudiante]
1	17
2	21
3	19

día	1	2	3	4
temperatura[día]	28.6	24.9	26.5	25.1

i	0	1	2	3
día	1	2	3	4
temperatura[día]	28.6	24.9	26.5	25.1

Categoría: Unidades

Matrices en programación con Numpy-Python

Algoritmos sobre Matrices en Análisis y Métodos Numéricos

Interpretación de matrices

1. Tarea

2. Ejemplo 1 - Secuencia de Fibonacci

Algoritmo en Python

3. Ejemplo 2 - números primos

Algoritmo en Python

Tarea

4. Ejemplos - Ejercicios resueltos de vectores

Vectores - Arreglos unidimensionales con Python y Numpy

Arreglos unidimensionales y números aleatorios

Arreglos, acumuladores y contadores

Arreglos en algoritmos

Bloque de Ingreso

Indices en arreglos

Bloque de procedimiento

Bloque de Salida

Ejemplos: ejercicios resueltos con bases numéricas

Actividades independientes

1. Número Decimal a Binario

2. Ejercicio: Cinco en binario

3. Algoritmo Decimal a Binario

Algoritmo en Python

Ejercicios:

1. Binario a Decimal

2. Ejercicio: Convertir a decimal el binario 101

3. Algoritmo de Binario a Decimal

Algoritmo en Python

Base Numérica Decimal

Ejercicios resueltos con Números Aleatorios, random()

Ejercicios resueltos de Algoritmos con aleatorios,

Actividades independientes con números aleatorios

Ejemplo de número aleatorios para un dado en Python

Ejercicio 1

Desarrollo

Instrucciones en Python