8.2.1 Gráficas 3D en Python – Fundamentos de Programación

Gráficas 3D: [ planos ] [ wireframe] [ scatter ] [ sólido revolución ]
..

1. Gráficas 3D en Python. Sistema de ecuaciones y Planos

El ejercicio se presenta desde la perspectiva que la solución es un punto de intersección de los planos en el espacio dados por cada ecuación. Ejercicio de métodos numéricos.

Ejercicio: Métodos numéricos en sistema de ecuaciones
Sistema de ecuaciones 3×3, planos 3D con Python

Gráficas 3D: [ planos ] [ wireframe] [ scatter ] [ sólido revolución ]
..

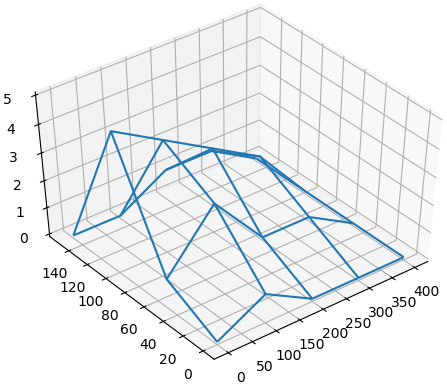
2. Gráficas 3D malla / wireframe

Usada cuando se tienen muestras de puntos f(x,y) y se dan los valores en cada eje x y eje y.

Ejemplo:

isla = np.array([[0,1,0,0,0],
                 [1,3,1,1,0],
                 [5,4,3,2,0],
                 [0,0,1,1,0]])

xi = np.array([0,100,200,300,400])
yi = np.array([0, 50,100,150])

la grafica requiere importar las librerias en 3D

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d

crea las matrices de puntos de referencia:

X, Y = np.meshgrid(xi, yi)

crea la gráfica en una figura con proyección 3D

figura = plt.figure()
ax = figura.add_subplot(111, projection = '3d')
ax.plot_wireframe(X,Y,isla)
plt.show()

con lo que obtiene:

Ejercicio: Métodos numéricos, para la unidad de integración numérica:
2Eva_IIT2011_T1_MN Volumen de lago

Gráficas 3D: [ planos ] [ wireframe] [ scatter ] [ sólido revolución ]
..

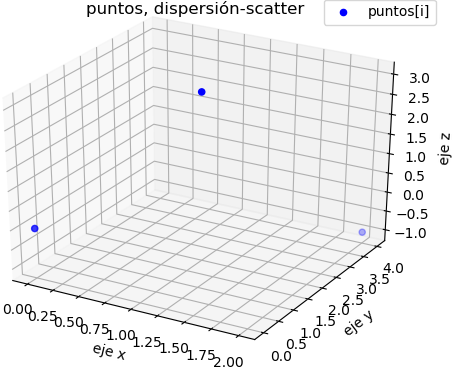
3. Gráficas 3D puntos dispersos / scatter

Varios puntos en el espacio para graficar, los puntos se ordenan por filas. Cada fila contiene las coordenadas [x, y, z] de cada punto:

puntos = np.array([[x0, y0, z0],
                   [x1, y1, z1],
                   [x2, y2, z3]])

Se usa un vector para cada coordenada xi, yi, zi.

xi = [x0, x1, x2]
yi = [y0, y1, y2]
zi = [z0, z1, z2]

con lo que se crea la gráfica de puntos (scatter) en 3d:

las instrucciones en Python son:

# Puntos en el espacio, Dispersión-Scatter
# cada fila representa un punto [xi,yi,zi]
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# INGRESO
# unpunto = [x,y,z]
puntos = np.array([[0, 0, 0],
                   [1, 2, 3],
                   [2, 4,-1]])

# SALIDA
# grafica
figura = plt.figure()
grafica = figura.add_subplot(111,projection = '3d')

# xi = [:,0] ; yi = [:,1], zi = [:,2]
# selecciona columnas, use la transpuesta de puntos
[xi, yi , zi] = np.transpose(puntos)

grafica.scatter(xi,yi,zi,
                c = 'blue',
                marker='o',
                label = 'puntos[i]')
grafica.set_title('puntos, dispersión-scatter')
grafica.set_xlabel('eje x')
grafica.set_ylabel('eje y')
grafica.set_zlabel('eje z')
grafica.legend()
plt.show()

siguiendo el esquema, se pueden añadir los puntos que sean necesarios.

Gráficas 3D: [ planos ] [ wireframe] [ scatter ] [ sólido revolución ]

4. Gráficas 3D sólidos de revolución

El ejercicio se presenta desde la perspectiva que un sólido que se genera al rotar un área que se encuentra entre f(x) y el eje x.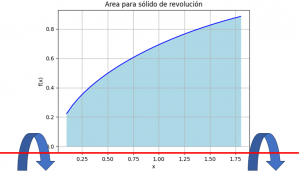

f(x) = \sqrt{\sin (x/2)}

El volumen del sólido de revolución se puede encontrar usando el integral

V = \int_{a}^{b} \pi (f(x))^2 dx

La gráfica del volumen de rotación se representa como: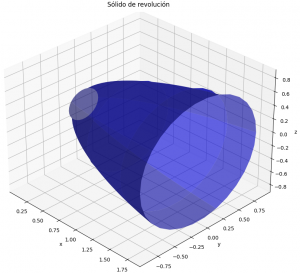

que se desarrolla usando la librería mpl_toolkits.mplot3d.axes3d

Se usa una figura(ventana) con una gráfica para 2D y otra figura para 3D

Instrucciones en Python

# 2Eva_2023PAOII_T1 Volumen por solido de revolución
# https://blog.espol.edu.ec/analisisnumerico/2eva_2023paoii_t1-volumen-por-solido-de-revolucion/
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d

# INGRESO
f = lambda x: np.sqrt(np.sin(x/2))

# eje x
xa = 0.1
xb = 1.8
xmuestras = 31
# angulo w de rotación
w_a = 0
w_b = 2*np.pi
w_muestras = 31

# PROCEDIMIENTO
# muestras en x
xi = np.linspace(xa, xb, xmuestras)

# grafica 2D para el area de corte en eje y,x
fi = f(xi)
f0 = np.zeros(xmuestras,dtype=float)

# grafica 3D muestras en x y angulo w
wi = np.linspace(w_a, w_b, w_muestras)
X, W = np.meshgrid(xi, wi)
# proyeccion en cada eje 
Yf = f(xi)*np.cos(W)
Zf = f(xi)*np.sin(W)

# SALIDA
# grafica 2D
fig_2D = plt.figure()
graf_2D = fig_2D.add_subplot(111)
graf_2D.plot(xi,fi,color='blue',label='f(x)')
graf_2D.fill_between(xi,fi,f0,color='lightblue')
graf_2D.grid()
graf_2D.set_title('Area para sólido de revolución')
graf_2D.set_xlabel('x')
graf_2D.set_ylabel('f(x)')

# grafica 3D
fig_3D = plt.figure()
graf_3D = fig_3D.add_subplot(111, projection='3d')

graf_3D.plot_surface(X, Yf, Zf,
                     color='blue', label='f(x)',
                     alpha=0.6, rstride=6, cstride=12)

graf_3D.set_title('Sólido de revolución')
graf_3D.set_xlabel('x')
graf_3D.set_ylabel('y')
graf_3D.set_zlabel('z')
# grafica.legend()
eleva = 30
rota = -45
deltaw = 5
graf_3D.view_init(eleva, rota)

# rotacion de ejes
for angulo in range(rota, 360+rota, deltaw ):
    graf_3D.view_init(eleva, angulo)
    plt.draw()
    plt.pause(.001)
plt.show()

Referencia: Sólido de revolución. Wikipedia. https://es.wikipedia.org/wiki/S%C3%B3lido_de_revoluci%C3%B3n

Ejercicio: métodos numéricos, para la unidad de integración numérica: 2Eva_2023PAOII_T1 Volumen por solido de revolución

Gráficas 3D: [ planos ] [ wireframe] [ scatter ] [ sólido revolución ]