Algoritmos 101

Cursos Python

Etiqueta: aleatorios

random, números aleatorios

  • 2Eva_IIT2008_T1 Carrera de caracoles

    2da Evaluación II Término 2008-2009. Febrero 10, 2009 /ICM00794

    Tema 1 (20 puntos) Para una carrera de n caracoles se coloca cada uno al inicio de una pista de 100 cm. caracolescarrera

    Cada minuto cada uno de ellos avanza aleatoriamente -1, 0, 1, 2, o 3 cm.

    Realice un programa que:

    • simule la carrera,
    • muestre en que minuto terminará la carrera y
    • cual es el caracol ganador.

    Nota: Pueden haber empates.
    Sugerencia: Almacene en un vector la distancia recorrida por cada caracol.

    Rúbrica: Simulación (10 puntos), control de carrera(5 puntos), ganador(5 puntos)

  • 2Eva_IT2008_T1 Juego 21 modificado

    2da Evaluación I Término 2008-2009. Septiembre 2, 2008 /ICM00794

    Tema 1. (25 puntos). Escriba un programa de simulación del juego “21 modificado”, donde el usuario sea el “primer jugador” y otro jugador “Banco” sea simulado por el computador, al final indique el resultado del juego acorde con las siguientes reglas:

    • El Juego de cartas “21 Modificado” participa un “jugador” y el “Banco” que consiste en obtener la suma de las cartas más cercana a 21. Existe un mazo de 44 cartas, numeradas del 1 al 11 para cada tipo o “palo” (trébol, corazón rojo, corazón negro, diamante).
    • El “primer jugador” al pedir una carta, selecciona azar una carta del mazo de 44, quien acumula los puntos de la obtenida sin importar el tipo. El jugador decide si solicita otra carta o se queda con la suma de puntos obtenida. El jugador puede solicitar cartas mientras no pase de 21 puntos acumulados. (10 puntos)
    • Al terminar el primer jugador, continúa el “Banco” que selecciona al azar 3 cartas del mazo. Si la suma de puntos es inferior a 12, se añade al azar otra carta. (5 puntos)
    • El jugador que consigue 21 puntos o la cantidad más cercana a 21 gana el juego; existe la posibilidad de empate o que ambos pierdan al sobrepasar los 21 puntos. (10 puntos)

  • 2Eva_IIT2007_T2 Juego de memotest

    2da Evaluación II Término 2007-2008. Febrero 12, 2008 /ICM00794

    Tema 2. (25 puntos) Memotest es un juego de tablero que consiste en buscar las “parejas”. El tablero cuadrado de tamaño 4×4, donde se encuentran ubicados de forma aleatoria números del 1 al 8 en fichas “volteadas” que no muestran el número. memotest

    • El juego consiste en indicar las ubicaciones de dos fichas en el tablero (fila y columna), que muestran su número y de resultar “parejas” se gana 10 puntos.
    • El jugador tiene máximo 3 posibilidades de equivocación para tratar de descubrir las 8 parejas.

    Escriba un programa en Matlab que permita simular el juego memotest.

    El programa pone parejas de números del 1 al 8 aleatoriamente en una matriz cuagrada de 4×4 equivalente al tablero de juego. Realice esta sección como una función tableroparejas(n) con n=4.

    Se pregunta al jugador dos posiciones de fichas que desea jugar, es decir filas y columnas en el tablero. El  algoritmo verifica si se ha encontrado una pareja de números o si se ha equivocado, revisando que no se puede equivocar más de 3 veces.

    Al final muestra la cantidad de puntos conseguidos.

    >>tableroparejas(4)
[[3 5 8 1]
 [4 3 2 6]
 [8 7 2 4]
 [6 7 1 5]]
>>>

    Rúbrica: generar tablero (5 puntos), función estructurada (3 puntos), validar casillas del jugador (2 puntos), equivocaciones (5 puntos), control de aciertos  o puntaje (5 puntos). Algoritmo estructurado (5 puntos)

  • 2Eva_IIT2007_T1 Palabras aleatorias alternando vocal y consonante, genword

    2da Evaluación II Término 2007-2008. Febrero 12, 2008 /ICM00794

    Tema 1. (25 puntos) Elabore una función GenWord para generar palabras conformadas de n letras escogidas de forma aleatoria, que pueden ser válidas o no en el idioma español.

    Para realizar la función se sugiere conformar una palabra de n letras, empezando con vocal o consonante y luego alternando entre vocal y consonante. Las letras se escogerán entre un arreglo de vocales y un arreglo de consonantes.

    Elabore un programa que permita:

    a) Leer y validar la cantidad de m palabras a generar.
    b) Para cada palabra generada, llamando previamente a la función GenWord, pedir al usuario si la palabra es válida o no.
    c) Mostrar el total de palabras válidas encontradas.

    Ingrese la cantidad de palabras: 4
Palabra generada: VELA
Desea aceptarla (1: Si, 0: No): 1
Palabra generada: IBUX
Desea aceptarla (1: Si, 0: No): 0
Palabra generada: ADAN
Desea aceptarla (1: Si, 0: No): 1
Palabra generada: CARO
Desea aceptarla (1: Si, 0: No): 1
total de palabras válidas: 3

    Referencia: Mono infinito. https://es.wikipedia.org/wiki/Teorema_del_mono_infinito

  • 2Eva_IT2007_T3 Simular carrera de perros

    2da Evaluación I Término 2007-2008. Agosto 28, 2007 /ICM00794

    Tema 3. (30 puntos) Diez perros se encuentran participando en una carrera, el recorrido que deben realizar es de un total de 100 metros con obstáculos, bajo las siguientes reglas: carreraperros

    • Todos avanzan al mismo tiempo.
    • Cada perro realiza aleatoriamente una de las 4 acciones siguientes:
      • salta 1 metro, o derribando o sorteando apropiadamente el obstáculo,
      • salta 2 metros, o derribando o sorteando apropiadamente el obstáculo.
    • Cuando el perro derriba un obstáculo, usted debe considerar que no puede avanzar en el siguiente instante de tiempo, porque tiene que recuperarse para el siguiente salto.

    Elabore un programa que simule el recorrido de los perros y muestre:

    a) El avance de los perros en la carrera, en cada instante de tiempo, hasta que terminó.
    b) El perro que ganó la carrera y la cantidad de saltos que necesitó para lograrlo (suponga que fue un solo perro).

     

  • 2Eva_IT2006_T2 Simula juego de ruleta, punto y premio

    2da Evaluación I Término 2006-2007. Agosto 29, 2006 /ICM00794

    Tema 2. (35 puntos) En la siguiente ruleta en su posición original encuentran ubicadas en casillas los puntajes 2, 7, 5, 9, 1, 3, 8 y 4 respectivamente y que son visibles al jugador.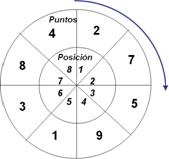

    En cada jugada, el participante apunta a (escoge) una casilla a la cual disparar, mientras que la ruleta gira posiciones aleatorias de 1 a 8 casillas a la derecha de forma rotativa.

    La ruleta gira, y gana los puntos dados en la posición donde el jugador decidió apuntar.

    Para cada jugada, la ruleta vuelve a su posición original.

    Luego de vario intentos, se muestra el resultado de los puntos acumulados obtenidos en cada disparo, y de acuerdo a los puntos acumulados, recibe uno de los premios de la tabla:

    Puntos Acumulados Premios
    5 a 15 Pluma
    16 a 35 Camiseta
    36 a 45 Balón del Mundial

    a) Escriba una función denominada puntoganado(posición) que recibiendo el elemento posición de disparo escogido por el jugador, retorne los puntos ganados obtenidos con el desplazamiento aleatorio de la ruleta. (15 puntos)

    b) Escriba una función denominada premio(acumulados), que reciba la cantidad de puntos acumulados y presente la descripción del premio correspondiente. (10 puntos)

    c) Escriba un programa en matlab que simule el juego si para cada jugador se le permite 5 disparos, y muestre al final el premio obtenido (use las funciones anteriores). (10 puntos)

    Rúbrica: literal a, definir la función (5 puntos), uso de aletorio (5 puntos), corrección de puntos por giro (5 puntos), literal b, producto predeterminado (2 puntos), uso de intervalos (8 puntos), literal c, usando las funciones (10 puntos)

  • 3Eva_IT2013_T2 sorteo de consejeros para estudiantes

    3ra Evaluación I Término 2013-2014, Septiembre 10, 2013 /ICM00794

    Tema 2 (25 puntos). Para asignar un consejero a cada estudiante, la universidad los selecciona de forma aleatoria buscando mantener el mismo número de estudiantes por cada consejero.

    http://www.vra.espol.edu.ec/content/estudiantes
    http://www.vra.espol.edu.ec/content/estudiantes

    Se dispone de n estudiantes y m profesores con dedicación tiempo completo que serán los consejeros.

    Realice una función sorteoconsejeros(n,m), que realice la asignación descrita

    >> sorteaconsejero(9,3)
ans = 1 3 1 1 2 3 3 2 2
 
>> sorteaconsejero(11,3) 
ans = 2 3 2 1 3 2 1 1 3 2 1

    Rúbrica: Definición de función (5 puntos), sorteo equitativo (10 puntos), sorteo fuera de equidad (10 puntos)

    Referencia: http://www.abet.espol.edu.ec/noticias/historico/17-noviembre-2008/35-consejerias-academicas.html

    Consejeros
    Profesor 1 2 3
    conteo
    asignados    		 3 3 3
    Estudiantes
    matricula 1 2 3 4 5 6 7 8 9
    consejero 1 3 1 1 2 3 3 2 2

  • 2Eva_IT2013_T1 Función sorteoentre(k,a,b)

    2da Evaluación I Término 2013-2014, Agosto 27, 2013 /ICM00794

    Tema 1. (15 puntos) Realice una función sorteoentre(k,a,b) que selecciona k números aleatorios no repetidos en el rango comprendido entre a y b.
    La función entrega un vector ordenado en forma ascendente.

    >> sorteoentre(5,1,15)
ans = 2 4 6 7 8
>> sorteoentre(5,16,30)
ans = 16 19 22 25 26

    No use las funciones definidas en MATLAB.

    Rubrica: Definición de función (5 puntos), generar vector no repetidos (5 puntos), vector ordenado (5 puntos)

    propuesta: s2Eva_IT2013_T2 Una Tabla de Bingo con arreglos

  • 1Eva_IIT2013_T4 Sorteo series mundial de fútbol

    1ra Evaluación II Término 2013-2014. Diciembre 3, 2013 /ICM00794

    Tema 4. (30 puntos) Una vez conocidas las 32 selecciones que participarán del próximo mundial de fútbol se necesita realizar el sorteo entre las 8 series o grupos de competencia.

    Las selecciones se encuentran numeradas del 1 al 32, las mejores han sido pre asignadas como “cabeza de serie”; una por cada grupo y no se sorteará su ubicación en la serie.

    Las selecciones restantes se sortearán la ubicación en cada serie (grupo) para completar los cuatro participantes por serie.

    grupo 1 2 3 4 5 6 7 8
    cabeza [grupo] 3 7 9 12 22 25 26 30

    El sorteo de serie (luego de copiar los cabezas de grupo) ser realizará en un vector como el mostrado:

    selección 1 2 3 4 5 6 7 8 9 ... 32
    serie [selección] 0 0 1 0 0 0 2 0 3 ... 0

    Elabore un algoritmo que solicite cuáles son los 8 equipos que serán cabezas de serie, asigne aleatoriamente (y sin repeticiones) los 24 equipos restantes, al final muestre el listado de las series resultantes.

    Rúbrica: Ingreso (5 puntos), definir pre-asignados (5 puntos), sorteos no repetidos (15 puntos), presentación de resultados (5 puntos).

  • 1Eva_IT2013_T3 Generar tarjetas pre pago

    1ra Evaluación I Término 2013-2014, Julio 2, 2013 /ICM00794

    Tema 3. (20 puntos) Una tarjeta prepago que se activa y valida por llamada telefónica o internet utiliza dos números: tarjeta prepago dibujo

    • la serie y
    • una clave

    ambos números hacen única a la tarjeta y se usan como método de registro y seguridad.

    La serie  se compone de 8 dígitos que corresponden a la identificación de la tarjeta dentro de un rango de producción, la clave es un número de 6 dígitos generados de forma aleatoria [100000, 999999];

    Elabore un algoritmo que permita
    a) generar n tarjetas prepago dentro de un rango de serie con su correspondiente clave de validación.
    b) Muestre cuántas tarjetas tienen claves impares y cuántas pares.
    c) Muestre la tabla de las series y sus claves

    Ejemplo:
    ¿Cuántas tarjetas?: 1000
    ¿Serie Inicial?:  2531 1001    		 Tarjeta Serie Clave
    1 2531 1001 725 673
    2 2531 1002 428 095
    ... ... ...
    1000 2531 2000 152 652

    Rúbrica: Ingreso (5 puntos), literal b (10 puntos), literal c (5 puntos).