Tema 2 (25 puntos). La función densidad conjunta de dos variables aleatorias está dada por:
f_{XY}(x,y) = k e^{-x} e^{-2y} 0 \leq y \leq x \leq \inftydeterminar:
a) P[y ≥ x/2]
b) E[Y|x=3]
Tema 1 (25 puntos). Dado FX(x) en la figura y Y=X2, determine:
a) P(x=1) y P(x≤-0.5)
b) Dibuje FY(y)
c) el valor esperado E[Y]
Tema 3 (30 puntos). Dada la siguiente función de Autocorrelación Rx(ζ) del proceso estocástico X(t) que es WSS.
a) (15 puntos) Encuentre Var[X(t)]
b) (15 puntos) Sx(w) ( o Sx(f))
Transformadas de Fourier
x(t) \rightarrow X(\omega) g(t) \rightarrow \int_{-\infty}^{\infty} g(t) e^{-j2 \pi ft} dt rect\left( \frac{t}{\tau}\right) \rightarrow \tau sinc\left( \frac{\omega \tau}{2}\right) tri\left( \frac{t}{\tau}\right) \rightarrow \frac{\tau}{2} sinc^2(\frac{\omega \tau}{4})Tema 2 (35 puntos). Sean A y Θ variables aleatorias independientes, A con distribución exponencial de media 1, y Θ con distribución uniforme en el intervalo (0, π/2), es decir las funciones de densidad de A y B son respectivamente:
f_A(a) = e^{-a} , a \in [0,\infty) T_{\Theta}(\theta) = \frac{2}{\pi} , \theta \in [0,\pi /2 ]Sea X(t) un proceso estocástico definido por:
X(t) = e^{-At}cos(\pi t + 4 \Theta) ; t>0Calcular:
a) La media y la autocorrelación del proceso X(t).¿Es el proceso estacionario en sentido amplio?
b) La varianza de X(t) y la covarianza entre X(1) y X(2).
c) La función de densidad de probabilidad para X(0)
cos(a ± b) = cos(a)cos(b) ∓ sen(a) sen(b)
Rúbrica: literal a (10 puntos, literal b (10 puntos), literal c (15 puntos)
Tema 1 (35 puntos). Para las variables aleatorias x,y con la siguiente función densidad conjunta:
f_{XY} (x,y) =\begin{cases} k(x+y) && 0.5 \leq y \leq x , 0.5\leq x\leq 1 \\ 0 && \text{otro caso}\end{cases}Encuentre:
a) (15 pts) Las funciones de densidad marginal de probabilidad, fx(x) y fy(y).
b) (10 Pts) Calcule P[x+y > 3/2].
c) (10 Pts) Calcule P\left[ \frac{Y\leq 0.75}{X+Y \geq 1.5}\right]
Tema 4 (20 puntos).Un proceso estocástico consiste de cuatro funciones del tiempo:
X(t, \xi_1) = 1 X(t, \xi_2) = cos(t) X(t, \xi_3) = sen(t) X(t, \xi_4) = e^{-|t/\pi|}cada una con probabilidad 0.1, 0.25, 0.3, 0.35 respectivamente.
Dibuje las funciones de tiempo (en forma aproximada)
a) Dibuje la función de distribución y la función densidad de probabilidad de la variable aleatoria definida a t=π, esto es, X1=X(t=π).
b) ¿Es este proceso estacionario de orden 1? Demostrar cualquiera que sea su respuesta
Tema 3 (30 puntos). Un proceso aleatorio estacionario en sentido amplio X(t) con densidad espectral de potencia:
\Im_{XX}(\omega) = 50 \pi \delta(\omega) + \frac{3}{1+\left(\frac{\omega}{2}\right)^2}se aplica a una red con respuesta impulso
h(t) = 2 e^{-2t} \mu (t)obteniendo luego de la red Y(t)
Determine:
a) Var[X(t)]
b) La densidad espectral de potencia de la respuesta de Y(t)
c) La potencia de Y(t)
Pares de Transformadas de Fourier:
x(t) \leftrightarrow X(\omega) 1 \leftrightarrow 2 \pi \delta(\omega) e^{-at}\mu (t) \leftrightarrow \frac{1}{a+j\omega} te^{-at}\mu (t) \leftrightarrow \frac{1}{(a+j\omega)^{2}} t^{n}e^{-at}\mu (t) \leftrightarrow \frac{n!}{(a+j\omega)^{n+1}} a>0Tema 2 (20 puntos). Se ha calculado la suma de una lista de 100 números reales .
Suponga que los números se redondean al entero más cercano de tal manera que cada número tiene un error que está distribuido uniformemente en el intervalo (-0.5, 0.5).
Usando el teorema del límite central estime la probabilidad de que el error en la suma exceda de 6.
Q(x) = \frac{1}{\sqrt{2 \pi}} \int_{x}^{\infty} e^{-t^2 /2} dt| x | Q(x) | x | Q(x) | |
|---|---|---|---|---|
| 0 | 5.00E-01 | 2.7 | 3.47E-03 | |
| 0.1 | 4.60E-01 | 2.8 | 2.56E-03 | |
| 0.2 | 4.21E-01 | 2.9 | 1.87E-03 | |
| 0.3 | 3.82E-01 | 3.0 | 1.35E-03 | |
| 0.4 | 3.45E-01 | 3.1 | 9.68E-04 | |
| 0.5 | 3.09E-01 | 3.2 | 6.87E-04 | |
| 0.6 | 2.74E-01 | 3.3 | 4.83E-04 | |
| 0.7 | 2.42E-01 | 3.4 | 3.37E-04 | |
| 0.8 | 2.12E-01 | 3.5 | 2.33E-04 | |
| 0.9 | 1.84E-01 | 3.6 | 1.59E-04 | |
| 1.0 | 1.59E-01 | 3.7 | 1.08E-04 | |
| 1.1 | 1.36E-01 | 3.8 | 7.24E-05 | |
| 1.2 | 1.15E-01 | 3.9 | 4.81E-05 | |
| 1.3 | 9.68E-02 | 4.0 | 3.17E-05 | |
| 1.4 | 8.08E-02 | 4.5 | 3.40E-06 | |
| 1.5 | 6.68E-02 | 5.0 | 2.87E-07 | |
| 1.6 | 5.48E-02 | 5.5 | 1.90E-08 | |
| 1.7 | 4.46E-02 | 6.0 | 9.87E-10 | |
| 1.8 | 3.59E-02 | 6.5 | 4.02E-11 | |
| 1.9 | 2.87E-02 | 7.0 | 1.28E-12 | |
| 2.0 | 2.28E-02 | 7.5 | 3.19E-14 | |
| 2.1 | 1.79E-02 | 8.0 | 6.22E-16 | |
| 2.2 | 1.39E-02 | 8.5 | 9.48E-18 | |
| 2.3 | 1.07E-02 | 9.0 | 1.13E-19 | |
| 2.4 | 8.20E-03 | 9.5 | 1.05E-21 | |
| 2.5 | 6.21E-03 | 10.0 | 7.62E-24 | |
| 2.6 | 4.66E-03 |
Tema 1 (30 puntos). Asuma un proceso estocástico estacionario en el sentido amplio X(t) con función de autocorrelación
R_X(t) = e^{-|t|} t \in \Rea) Determine la densidad espectral de potencia del proceso
A(t) = X(t) - X(t-1)Si se define el proceso estocástico
B(t) = X(t) cos(t+ \rho)donde ρ es una variable aleatoria independiente de X(t) con distribución uniforme en el intervalo (0, π), determine:
b) Es B(t) estacionario en el sentido amplio
c) La mínima diferencia de tiempos para la cual dos variables aleatorias de B(t) son independientes entre sí.
Indicación: 2 cos(a) cos(b) = cos(a + b) + cos(a − b)
Referencia: Leon W Couch 4-2 p234, "El Aguacate" introducción
La modulación es el proceso de codificación de la información fuente, sonido o moduladora, dentro de una señal pasabanda s(t), resultande o modulada. La señal modulada se obtiene de:
senal(t) = A_c[1+moduladora(t)] cos(\omega_c t) s(t) = A_c[1+m(t)] cos(\omega_c t)
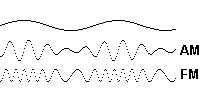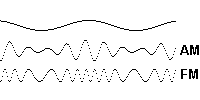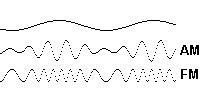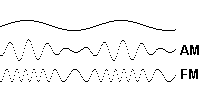
donde:
\omega_c = 2\pi f_cfc es la frecuencia de la portadora o "carrier".
Ac es la amplitud de la portadora.
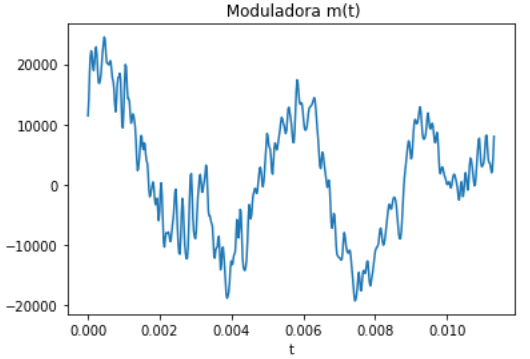
Como ejemplo, si se quiere enviar una señal de sonido obtenida de un archivo.wav modulada en Amplitud, la señal m(t) será:
# pmf de un sonido # entrada es archivo01 # propuesta:edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import scipy.io.wavfile as waves import scipy.stats as stats # INGRESO # archivo01 = input('archivo de sonido 01: ' ) # k = int(input('muestras para ejemplo: ')) archivo01 = 'muestra_GuitarraCuerda.wav' k = 500 # PROCEDIMIENTO muestreo, sonido01 = waves.read(archivo01) # Extrae un canal en caso de estéreo canales = sonido01.shape cuantos = len(canales) canal = 0 if (cuantos==1): # Monofónico uncanal = sonido01[:] if (cuantos>=2): # Estéreo uncanal = sonido01[:,canal] moduladora = uncanal[0:k].astype(float) dt = 1/muestreo t = np.arange(0,k*dt,dt) # SALIDA GRAFICA plt.plot(t,moduladora) plt.title(' Moduladora m(t)') plt.xlabel('t') plt.ylabel('señal') plt.plot() plt.show()
Para el ejemplo, la señal de la portadora presentada tiene frecuencia de 5500 para que se pueda visualizar el efecto.
(Revisar frecuencias de portadoras AM estándares o ver el dial de un radio AM).
# Portadora: fc = 5500 portadora = np.cos(2*np.pi*fc*t) # SALIDA GRAFICA plt.plot(t,portadora, color='orange') plt.title(' Portadora') plt.xlabel('t') plt.ylabel('señal') plt.plot() plt.show()
Antes de aplicar la moduladora, se la normaliza para mantener la proporción en la gráfica
# normalizar y subir a positiva moduladoranorm = moduladora/np.max(moduladora) moduladora = (1+ moduladoranorm) # Modular portadora Ac = 1 modulada = Ac*moduladora*portadora # SALIDA GRAFICA plt.plot(t,moduladora,label='moduladora') plt.plot(t,modulada,label='modulada') plt.title(' Señal modulada S(t)') plt.xlabel('t') plt.ylabel('señal') plt.legend() plt.show()
