Tema 2
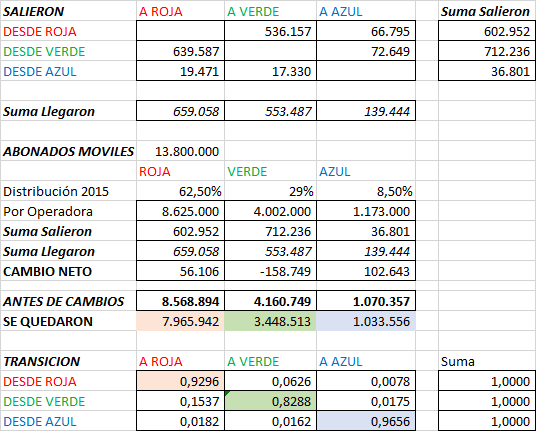
Cadena de Markov, desarrollo a partir del diagrama
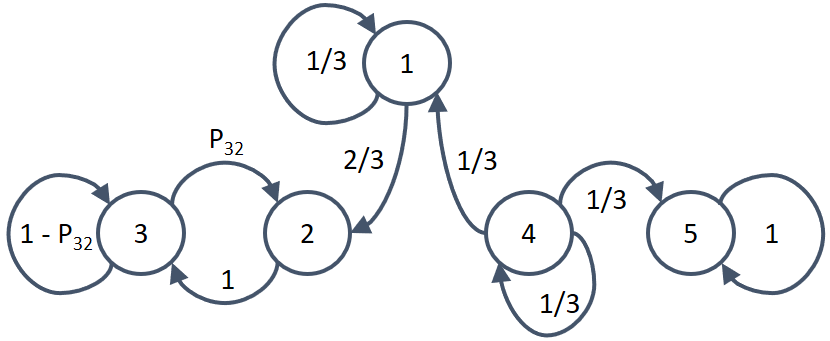
a) Identifique los estados transientes
estados 1 y 4
b) Identifique las clases de los estados recurrentes
estados 2 y 3 son de tipo recurrente m y el estado 5 es una clase (singlenton) o absorvente
c)Para cada clase recurrente, encuentre la probabilidad de estado estable \pi_i.
p = \begin{pmatrix} 1/3 & 2/3 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & P_{32}& 1-P_{32}& 0 & 0 \\ 1/3 & 0 & 0 & 1/3 & 1/3 \\ 0 & 0 & 0 & 0 & 1 \end{pmatrix}
para la clase {2,3} se tiene que:
\pi_{2} = \pi_{3}P_{32}
\pi_{3} = \pi_{2} + (1-P_{32}) \pi_{3}
1 = \pi_{2} + \pi_{3}
usando la ecuacion (1) en ecuacion (3)
1 = \pi_{3}P_{32} + \pi_{3}
1 = (P_{32} + 1) \pi_{3}
\pi_{3} = \frac{1}{(P_{32} + 1)}
que reemplazando en (1)
\pi_{2} = \frac{P_{32}}{(P_{32} + 1)}
en el caso de \pi_{5} = [0,0,0,0,1] por ser absorvente.
d) Encuentre las probabilidades de transición para n pasos Pnij como una función de n. Con sus palabras describa cada una (no requiere ecuaciones).
1. Pn44 = (1/3)n debido las transiciones a si misma, cada vez son mas pequeñas y tenderían a cero.
2. Pn45 = (1/3 + (1/3)2 + ... + (1/3)n = 1/2(1-(1/3)n). En el largo plazo solo hay dos opciones, o ir hacia 5 o ir hacia 1, por simetria de salida del estado 4.
3. Pn41 = n(1/3)n para cada n caminos para ir de 4 a 1 en n pasos, cada camino tiene una probabilidad de (1/3)n, pero debe tender a cero.
4. Pn43 + Pn42 = 1- Pn44- Pn45 - Pn41 = 1/2 - [(2n+1)/2] (1/3)n. Corresponde al otro camino complementario de ir al estado 5.
que debe ser distribuido entre la llegada al estado 2 y 3, que a su vez sumará 1/2.
5. de el caso anterior, el limite cuando n tiende a infinito, la suma de los estados 2 y 3 será 1/2. Usando el resultado del literal e, que sucedan las dos cosas implica multiplicar el pasar por la rama de 1, y lo que corresponde al estado 3, es decir:
\pi_{3} = \frac{1}{2} \frac{1}{(P_{32} + 1)}
OTRA FORMA, usando python
Se analiza el comportamiento a largo plazo, usando un valor para Pa , por ejemplo 0.5.
Para un exponente "grande" n=1000, se puede ver en la columna 4 lo que se escribió en la sección anterior, que solo hay dos caminos de salida ,y se distribuye la probabilidad por simetría en 0.5 y 0.5 hacia el estado absorvente {5} y el recurrente {2,3}
# Tema 2. diagrama de transicion
import numpy as np
a=0.5
p=np.array([
[1/3,2/3, 0, 0, 0],
[ 0, 0, 1, 0, 0],
[ 0, a,1-a, 0, 0],
[1/3, 0, 0,1/3,1/3],
[ 0, 0, 0, 0, 1]
])
n=1000
pn=np.linalg.matrix_power(p,n)
print(pn)
# Resolviendo por matrices A= AT-I) y el vector de ceros terminado en 1
k=len(p)
A=p.transpose()
A=A-np.identity(k, dtype=int)
# la última fila se sustitute por la suma de probabilidades
A[-1,:]=np.ones(k,dtype=int)
B=np.zeros(k,dtype=int)
B[-1]=1 # el último
Pncalc=np.linalg.solve(A,B)
print('largo plazo')
print(Pncalc)
[[ 0. 0.33333333 0.66666667 0. 0. ]
[ 0. 0.33333333 0.66666667 0. 0. ]
[ 0. 0.33333333 0.66666667 0. 0. ]
[ 0. 0.16666667 0.33333333 0. 0.5 ]
[ 0. 0. 0. 0. 1. ]]
largo plazo
[ 0. -0. 0. -0. 1.]
donde se pueden observar las clases...y los valores a largo plazo