Para que un modelo sea útil, se debe poder realizar predicciones del comportamiento del sistema en el futuro, es decir debe tener un comportamiento regular.
Muchos modelos de probabilidad en ingeniería se fundamentan en los promedios obtenidos en las secuencias de resultados, así las muchas repeticiones o intentos del experimento aleatorio son consistentes y tienden aproximadamente al mismo valor. 
Esta es la propiedad de regularidad estadítica.
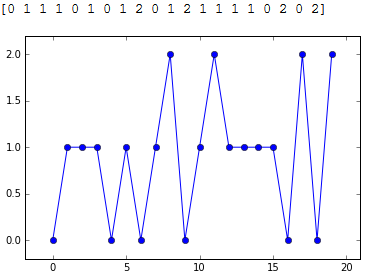
En el experimento de la urna y pelotas con S={0, 1, 2}, se pueden procesar las muestras del archivo: aleatoriosurna100.txt
muestras = [1,1,1,1,1,2,1,2,2,2,2,0,0,0,0,0,2,1,2,2,
0,2,0,2,1,2,1,2,2,0,2,0,1,2,0,2,2,0,2,1,
1,1,1,1,0,2,1,2,1,0,1,0,1,2,0,2,2,2,1,0,
2,2,0,2,0,2,1,1,0,0,2,1,0,1,0,0,2,1,2,0,
1,1,2,0,0,0,1,0,2,2,2,0,0,0,1,2,1,1,0,0]
Algoritmo en Python
Para seleccionar los valores únicos de las muestras y contar el número de veces de cada uno se puede usar la instrucción de numpy np.unique
los valores unicos: [ 0. 1. 2.]
la cuenta de unicos: [33 31 36]
Nk:
[[ 0. 33.]
[ 1. 31.]
[ 2. 36.]]
Instrucciones en Python
# Muestras de una urna con pelotas S=[0,1,2]
# propuesta: edelros@espol.edu.ec
import numpy as np
# INGRESO
# archivotxt=input('nombre del archivo.txt: ')
archivotxt = 'aleatoriosurna100.txt'
# PROCEDIMIENTO
muestras = np.loadtxt(archivotxt)
n = len(muestras)
# cuenta los únicos
[unicos,cuenta] = np.unique(muestras,return_counts=True)
# une en tabla N, y aplica T transpuesta
N = np.asarray((unicos, cuenta)).T
# SALIDA
print('los eventos unicos: ', unicos)
print('la cuenta de unicos: ', cuenta)
print('Nk:')
print(N)
El número de veces que aparece la pelota 0 en el experimento es N0(n)=33,la pelota N1(n)=31 y N2(n)=36.
Frecuencia relativa
La frecuencia relativa de un resultado k, se define como:
f_k(n)=\frac {N_k(n)}{n}
y lo que la regularidad estadística quiere decir es que fk(n) varía siempre acercandose a una constante pk cuando n tiende a ser muy grande.
lim_{n\to\infty} f_k(n) = p_k
# frecuencia relativa
fk = cuenta/n
fkn = np.asarray((unicos, fk)).T
print(fkn)
[[ 0. 0.33]
[ 1. 0.31]
[ 2. 0.36]]
Tarea
Repita el experimento de la urna con n=1000 intentos, y determine las frecuencias relativas de cada pelota. Use el algoritmo de la hoja "modelo de probabilidad" para generar el archivo de aleatorios
Ejercicios
Referencia: Gubner 1.1 p.18
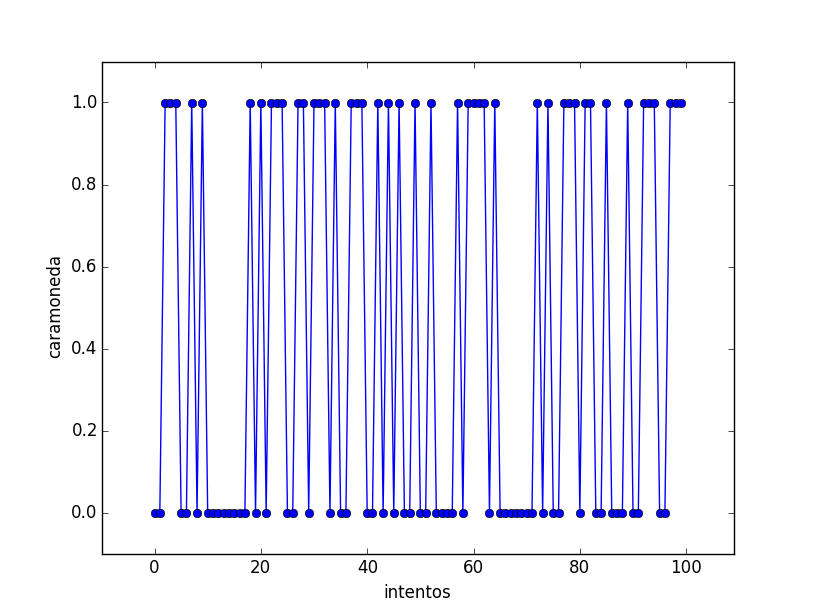
Se lanza una moneda 100 veces, y se anota la frecuencia relativa de las caras (0) y sellos (1). La experiencia nos indica que la frecuencia relativa debería estar alrededor de 0.5. Realice el experimento simulado y compare los resultados.
caras de moneda:
[0 0 1 1 1 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0
1 0 1 1 1 0 0 1 1 0 1 1 1 0 1 0 0 1 1 1
0 0 1 0 1 0 1 0 0 1 0 0 1 0 0 0 0 1 0 1
1 1 1 0 1 0 0 0 0 0 0 0 1 0 1 0 0 1 1 1
0 1 1 0 0 1 0 0 0 1 0 0 1 1 1 0 0 1 1 1]
frecuencia relativa:
[[ 0. 0.55]
[ 1. 0.45]]
# Simulador de lanza monedas [0,1]
# propuesta: edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
intentos = 100
eventos = 2
# PROCEDIMIENTO
# lanza moneda
caramoneda = np.random.randint(eventos,size=intentos)
# cuenta los únicos
[unicos, cuenta] = np.unique(caramoneda,return_counts=True)
# frecuencia relativa
fk = cuenta/intentos
# une en tabla fkn, y aplica T transpuesta
fkn = np.asarray((unicos, fk)).T
# SALIDA
print(' caras de moneda: ')
print(caramoneda)
print('frecuencia relativa:')
print(fkn)
# grafica pmf
plt.plot(caramoneda,'o--')
plt.xlabel('intentos')
plt.ylabel('caramoneda')
plt.margins(0.1)
plt.show()
Ejercicio
Referencia: Gubner 1.2 p.18, Leon-García pdf/p.21
Un experimento por si mismo es lanzar una moneda 100 veces y guardar las frecuencias relativas de cada caras.
Dado que el numero de caras puede estar en el rango entre 0 y 100, hay 101 posibilidades de respuesta.
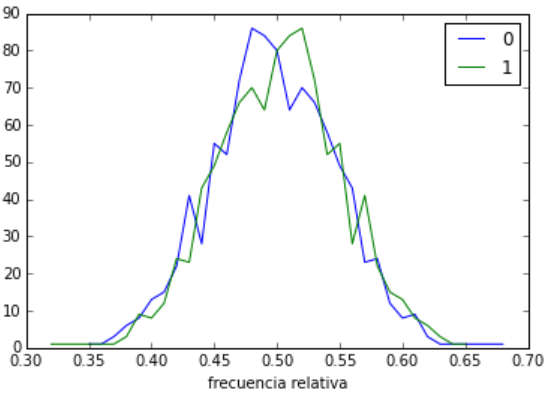
Realice el experimento anterior 1000 veces y almacene la frecuencia relativa para cada experimento. Muestre los resultados.
# Simulador de lanza monedas [0,1]
# Ejercicio: Gubner 1.2 p.18, Leon-García pdf/p.21
# propuesta: edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
experimentos = 1000
intentos = 100
eventos = 2
# PROCEDIMIENTO
# Para cada experimento
resultado = np.zeros(shape=(experimentos,eventos),dtype=int)
for i in range(0,experimentos):
# lanza moneda
caramoneda = np.random.randint(eventos,size=intentos)
n=len(caramoneda)
[unicos, cuenta] = np.unique(caramoneda,return_counts=True)
# resultado de cada experimento
for j in range(0,eventos):
resultado[i][j] = cuenta[j]
# Frecuencias relativas por evento
s = np.arange(eventos)
fr_cuenta = []
fr_unicos = []
for evento in s:
unevento = resultado[:,evento]
[unicos,cuenta] = np.unique(unevento,return_counts=True)
fr_cuenta.append(cuenta)
fr_unicos.append(unicos)
# SALIDA - gráfica
for evento in s:
plt.plot(fr_unicos[evento]/100,fr_cuenta[evento],label=str(evento))
plt.xlabel('frecuencia relativa')
plt.legend()
plt.show()
Tarea
Escriba sus observaciones en el ejercicio anterior, cambiando el número de intentos en el rango de [10, 100000].
Referencia: Leon-García 1.3 p.5, Gubner p.3