Procesos Estocásticos

Autor: Edison Del Rosario

  • PAM a PSK - valor esperado

    Y(t) = a \cos \big( 2\pi t + \frac{\pi}{2}X(t) \big)

    La pmf de x(t) es 0.5 para cada valor de [-1,1]

    c) Encuentre la media y autocorrelación de Y(t)

    E[Y(t)] = E\big[ a \cos \big( 2\pi t + \frac{\pi}{2}X \big)\big]

    Referencia:  León-García 3.3.1 p. 107. Valor esperado de funciones de variable aleatoria

    Si z =g(x)

    E[g(x)] = \sum_k g(x_k)p_x(X_k)

    se tiene entonces que:

    = \big[a \cos \big( 2\pi t + \frac{\pi}{2}(-1) \big)\big]\frac{1}{2} + \big[a \cos \big( 2\pi t + \frac{\pi}{2}(1) \big)\big] \frac{1}{2} = \frac{a}{2}\cos \big( 2\pi t - \frac{\pi}{2} \big) + \frac{a}{2}\cos \big( 2\pi t + \frac{\pi}{2} \big) = \frac{a}{2} \sin \big( 2\pi t \big) - \frac{a}{2} \sin \big( 2\pi t \big) = 0 E[Y(t)] = 0

  • PAM a PSK Gráfica

    Referencia: Problema 9.133 Leon-García p.574

    Un proceso de modulación por fase se define como:

    Y(t) = a \cos \big( 2\pi t + \frac{\pi}{2}X(t) \big)

    Sea X(t) un proceso de modulación de amplitud de pulsos con valores de +1 y -1 que representan a los bits 1 y 0 como se muestra en la tabla.

    dato en binario (bit) símbolo
    1 +1
    0 -1

    Suponga que T=1, que es la duración de cada símbolo X(t).

     

    Algunos datos:

    De los experimentos realizados con BPSK y Delta-Sigma para entrontrar la pmf de [+1,-1], se encontró que la media del proceso era igual a 0.

    a) Dibuje una muestra de la función Y(t) correspondiente a la secuencia binaria 0010110

    # Problema 9.133 Leon-Garcia p.574
# PAM - Pulse Amplitude Modulation
# PSK - Phase Shift Keying
# literal a)
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
# secuencia = input('secuencia binaria: ')
secuencia = '0010110'

# PROCEDIMIENTO
n = len(secuencia)
# texto a símbolos PAM
senalbit = np.zeros(n,dtype=int)
for i in range(0,n,1):
    senalbit[i] = int(secuencia[i])
    if (senalbit[i]==0):
        senalbit[i] = -1
# Señal en PAM
anchobit = 100 # muestras dentro de cada bit
senalpam = np.repeat(senalbit, anchobit)
m = len(senalpam)

# Eje de tiempo:
ti = np.arange(0,m,dtype=float)
ti = ti/anchobit

# Señal PSK
f = 1
senalpsk = np.zeros(m,dtype=float)
for i in range(0,m,1):
    fase = (np.pi/2)*senalpam[i]
    senalpsk[i] = np.cos(2*np.pi*f*ti[i] + fase)

# SALIDA Gráfica
# Señal PAM
plt.subplot(211)
plt.plot(ti,senalpam, color='g')
for k  in range(0,n,1):
    plt.vlines(k,1,-1, color= 'm', linestyles='dotted')
plt.ylabel('Señal PAM')
# Señal PSK
plt.subplot(212)
plt.plot(ti,senalpsk, color='b')
for k  in range(0,n,1):
    plt.vlines(k,1,-1, color= 'm', linestyles='dotted')
plt.ylabel('señal PSK')
plt.suptitle('Secuencia binaria PAM a PSK')
plt.show()

    continua...

  • Media y autocovarianza con t

    Referencia: Problema 9.13 Leon-García p.558 pdf 55

    El proceso aleatorio Z(t) definido por:

    Z(t) = 2Xt -Y

    donde X y Y son  variables aleatorias con medias mX, mY ,  varianzas σ2X y σ2Y y coeficientes de correlación ρXY.

    Encuentre la media y autocovarianza de Z(t)

    Solución propuesta:

    E[Z(t)] = E[ 2Xt - Y ]
    = 2E[X]t - E[Y]
    = 2tmX - mY = mZ
    CZ(t1, t2) = E[(2Xt1 - Y)(2Xt2 - Y)] - mZ(t1) mZ(t2)
    = E[ 4X2 t1t2 - 2XYt1   - 2XYt2 + Y2] 
      - (2t1mX - mY)(2t2mX - mY)
    = 4t1t2 E[X2] - 2t1 E[XY] - 2t2 E[XY] + E[Y2] 
      - (4t1t2m2X -2t1mXmY -2t2mXmY + m2Y)
    = 4t1t2 E[X2] - 2(t1 +t2)E[XY] + E[Y2] 
      -4t1t2m2X + 2(t1+2)mXmY - m2Y 
    = 4t1t2 (E[X2] - m2X ) - 2(t1 +t2)(E[XY] - mXmY) + (E[Y2] - m2Y)
    = 4t1t2 σ2X - 2(t1 +t2)σXY + σ2Y 

dado ρXY = σXY/σXσY
     ρXYσXσY = σXY

    = 4t1t2 σ2X - 2(t1 +t2) ρXYσXσY  + σ2Y 

σ2Z(t) = CZ(t, t) = 4t2σ2X - 4t ρXYσXσY + σ2Y

    Para X y Y solo se da la media y varianza, la función final debe tener la misma forma:
    f_{Z(t)} = \frac{e^{ -(z - m_Z)^2 /(2 \sigma_Z^2)}}{ \sqrt{2 \pi }\sigma_Z}

    f_{Z(t)} = \frac{e^{-\frac{(z - 2t m_{X} +m_{Y})^2 }{(2(4t^2\sigma_{X}^2 - 4t\sigma_{X} \sigma_{Y} \rho_{XY} + \sigma_{Y}^2)}}}{ \sqrt{2 \pi }\sqrt{4t^2\sigma_{X}^2 - 4t\sigma_{X} \sigma_{Y} \rho_{XY} + \sigma_{Y}^2}}

  • Correlación bits con ruido

    Dada una secuencia de bits, al transmitirlos se distorsionó con ruido aditivo. En el receptor será dificil discriminar los valores de los bits tomados de la señal recibida.

    La correlación permite "limpiar" un poco la señal en el receptor y una mejor estimación de los bits recibidos.

    Para el ejemplo se usa una secuencia de bits 01101001 como señal a transmitir, el ruido aditivo es de tipo normal con media m=0 y varianza σ2=1

    Para referencia del proceso, se usa un punto rojo en el centro de la ventana de tiempo de cada bit.

    La correlación se realiza con un bit y la señal con ruido.

    Observe que luego de la correlación es más sencillo discriminar si lo recibido fué un bit 0 o un bit 1.

    señal de bits sin ruido
[0 1 1 0 1 0 0 1]
estimado de bits en el receptor
[ 0.002  0.985  1.07   0.054  0.947 -0.079 -0.006  1.149]

    Instrucciones en Python

    # secuencia de bits con Ruido
# usar correlación para mejorar la senal
# estimar el bit recibido
# Tarea: convertir estimado en bits

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as st

# INGRESO

senalbit = np.array([0, 1, 1, 0, 1, 0, 0, 1])

# PROCEDIMIENTO

# señal moduladora son escalones por cada bit
# o forma rectangular de duración anchobit
anchobit = 128
mitadbit = anchobit//2
senal = np.repeat(senalbit, anchobit)
muestras=len(senal)

# reloj para observar la mitad del bit
reloj = np.arange(mitadbit, muestras, anchobit)

# Ruido normal o Gausiano
media = 0
varianza = 1
ruido = st.norm.rvs(media,varianza,muestras)

# Añade el ruido a la señal
senalruido = senal + ruido

# Referencia de un bit para correlación
modelo = np.ones(anchobit)

# correlación modelo de bits
correlacion = np.correlate(senalruido, modelo, mode='same')
# normaliza el resultado [0,1]
correlacion = correlacion / anchobit

# estimado de bits en el receptor
estimado=correlacion[reloj]

# SALIDA
print('señal de bits sin ruido')
print(senalbit)
print('estimado de bits en el receptor')
np.set_printoptions(precision=3)
print(estimado)

#GRAFICA
plt.figure(1)       # define la grafica
plt.suptitle('señal binaria con ruido gaussiano')

plt.subplot(311)
plt.plot(senal)
plt.plot(reloj, senal[reloj], 'ro')
plt.ylabel('señal original')
plt.margins(0,0.05)

plt.subplot(312)
plt.plot(senalruido)
plt.plot(reloj, senalruido[reloj], 'ro')
plt.ylabel('senal con ruido')
plt.margins(0,0.05)

plt.subplot(313)
plt.plot(correlacion)
plt.ylabel('correlación')
plt.plot(reloj, correlacion[reloj], 'ro')
plt.margins(0,0.05)

plt.show()

  • Correlación entre dos señales de audio

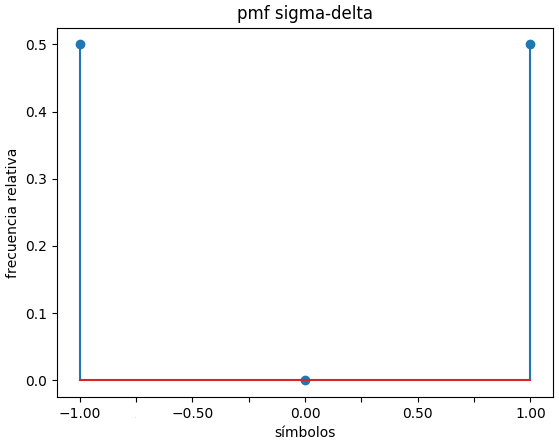
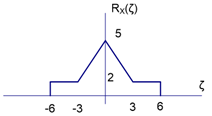
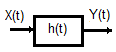
    Referencia: Archivos de Audio.wav – Abrir, extraer una porción

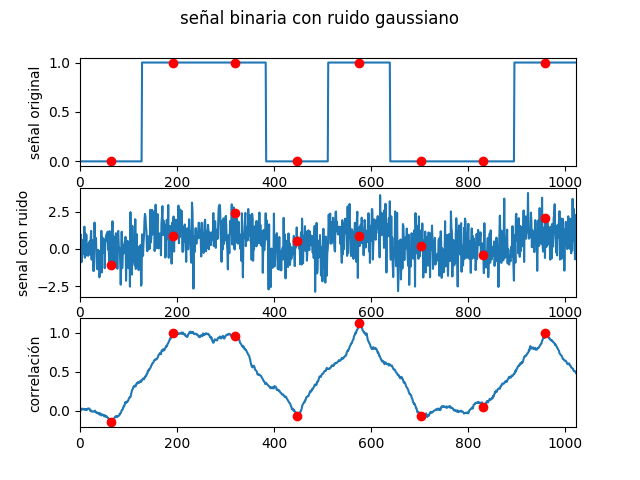
    Para comparar dos señales de sonido se puede usar la operación de correlación.

    Por ejemplo, usando dos archivos.wav, se compara las partes de una canción cantada por diferentes personas. Cada parte se obtiene de los archivos señal01 y señal02 semejantes a las siguientes:

    señal01: elaguacate_muestra01.wav
    señal02: elaguacate_muestra02.wav

    la correlación, destaca las partes en que las señales son semejantes como se muestra en la gráfica.

    Tarea: Realice las observaciones y recomendaciones al proceso, realizando el ejercicio con una canción diferente a la mostrada. Use la seleccionada para otras tareas.

    Instrucciones en Python

    Para el algoritmo, la primera señal de menor duración, la segunda es la señal de mayor duración.

    Las señáles se normalizan en el rango [0,1] previo a procesar la correlación.

    Para que las gráficas sean proporcionales en el eje de tiempo, a la señal01 se aumenta valores de cero o relleno.

    Puede quedar como tarea, convertir el eje x en unidades de tiempo en lugar del número de la muestra.

    # analiza correlación entre dos muestras
# supone que señal01 es más corta que señal02
# propuesta:edelros@espol.edu.ec

import numpy as np
import matplotlib.pyplot as plt
import scipy.io.wavfile as waves

# Un canal en caso de estereo
def extraeuncanal(sonido):
    canales=sonido.shape
    cuantos=len(canales)
    canal = 0
    if (cuantos==1): # Monofónico
        uncanal=sonido[:]
    if (cuantos>=2): # Estéreo
        uncanal=sonido[:,canal]
    return(uncanal)

# PROGRAMA
# INGRESO
# archivo01 = input('archivo de sonido 01:' )
# archivo02 = input('archivo de sonido 02:' )
archivo01 = 'elaguacate_muestra01.wav'
archivo02 = 'elaguacate_muestra02.wav'

muestreo, sonido = waves.read(archivo01)
senal01 = extraeuncanal(sonido)

muestreo, sonido = waves.read(archivo02)
senal02 = extraeuncanal(sonido)

# PROCEDIMIENTO
tamano01 = len(senal01)
tamano02 = len(senal02)

# Normaliza las señales
amplitud = np.max(senal01)
senal01 = senal01/amplitud
senal02 = senal02/amplitud

# Correlación para comparar
correlacion = np.correlate(senal01,senal02, mode='same')

# SALIDA
# unifica dimensiones de señal01 y señal02
extra = np.abs(tamano01-tamano02)
relleno = np.zeros(extra,dtype=float)
senal01relleno = np.concatenate((senal01,relleno),axis=0)
plt.suptitle('Correlación(señal01,señal02)')

plt.subplot(311)
plt.plot(senal01relleno,'g', label = 'señal01')
plt.legend()

plt.subplot(312)
plt.plot(senal02,'b', label = 'señal02')
plt.legend()

plt.subplot(313)
plt.plot(correlacion,'m', label = 'correlación')
plt.legend()

plt.show()

    Para extraer una porción de audio de un archivo.wav, revise las instrucciones en el tema:

    Referencia: Archivos de Audio.wav – Abrir, extraer una porción

  • 3Eva_IT2017_T4 densidad espectral de potencia

    3ra Evaluación I Término 2017-2018.  Septiembre 12, 2017

    Tema 4 (25 puntos). Dada la siguiente función de auto-correlación RX(ζ) del proceso estocástico X(t) que es estacionario en el sentido amplio (WSS).

    a) Determine la varianza X(t)

    b) Encuentre la densidad espectral de potencia

    c) Calcule la potencia promedio de X(t)

    Rúbrica: literal a (10 puntos), literal b(10 puntos) literal c (5 puntos)

  • 3Eva_IT2017_T3 Pdf conjunta, marginales, covarianza

    3ra Evaluación I Término 2017-2018.  Septiembre 12, 2017

    Tema 3 (20 puntos). La función densidad conjunta de X, Y es:
    f(x,y) = \frac{1}{y} e ^{-(y + x/y)}
    donde: 0<x<∞ , 0<y<∞ \

    a)    Verifique que es una función de densidad conjunta

    b)    Determine las funciones de densidad marginal

    c)     Encuentre la Covarianza(X, Y)

    Rúbrica: literal a y b (7 puntos), literal c (6 puntos)

     

  • 3Eva_IT2017_T2 pdf diente sierra

    3ra Evaluación I Término 2017-2018.  Septiembre 12, 2017

    Tema 2 (25 puntos). Dado el proceso o señal diente de sierra, descrito en la gráfica, con periodo π/3.

    Suponga que X es una variable aleatoria uniforme, distribuida en el intervalo de (0, π].

    a)    Determine la función densidad de probabilidad para Y

    b)    Calcule la función de distribución acumulada para Y

    c)     Grafique su resultado

    Rúbrica: literales a y b (10 puntos cada uno), literal c (5 puntos)

  • 3Eva_IT2017_T1 movilidad clientes supermercado

    3ra Evaluación I Término 2017-2018.  Septiembre 12, 2017

    Tema 1 (30 puntos). En una ciudad existen 3 cadenas de supermercados (X, Y, Z) y se dispone de la movilidad de los clientes entre ellos.

    En septiembre de un total de 1 millón de clientes, la cuarta parte realiza las compras en el supermercado X, 1/3 va al supermercado Y, mientras que 5/12 adquiere productos en el supermercado Z.

    En cada mes el supermercado X retiene el 90% de sus clientes y pierde el 10% que van al supermercado Y.

    Se determinó que del supermercado Y solo retiene el 5% de sus clientes y el 85% se cambian a X y el resto va a Z.

    El supermercado Z retiene solo el 40% de su clientela, el 50% va al supermercado X y el 10 % se cambia a Y.

    a) Determine los estados del problema

    b) Realice el diagrama de transición

    c) Elabore la matriz de transición correspondiente

    d) Clasifique los estados del problema

    e) Determine el vector de probabilidad estable

    f) ¿Cuál es la proporción de clientes para los supermercados al mes siguiente?

    g) Suponga que observa un cliente del supermercado Y:

    1.  Determine la probabilidad que en el siguiente periodo sea cliente de Z.
    2.  Luego el cliente del numeral anterior al segundo periodo decida cambiarse a X
    3.  Para un cliente de Y, determine la probabilidad que luego de tres periodos no termine comprando en X.

    Rúbrica: Literales a al f (4 puntos cada uno), literal g (6 puntos).

  • 2Eva_IT2017_T5 X(t) pasa por sistema h(t)

    2da Evaluación I Término 2017-2018. 29-Agosto-2017

    Tema 5 (10 puntos). Si el proceso estocástico X(t) del tema anterior pasa por un sistema con función de transferencia h(t)
    h(t) = 4 e^{-2t} \mu (t)
    a)    Determine la densidad espectral de potencia en la salida

    b)    Calcule la potencia promedio del proceso en la salida