Tema 4 (25 puntos). Dada la siguiente función de auto-correlación RX(ζ) del proceso estocástico X(t) que es estacionario en el sentido amplio (WSS). 
a) Determine la varianza X(t)
b) Encuentre la densidad espectral de potencia
c) Calcule la potencia promedio de X(t)
Rúbrica: literal a (10 puntos), literal b(10 puntos) literal c (5 puntos)
Tema 3 (20 puntos). La función densidad conjunta de X, Y es:
f(x,y) = \frac{1}{y} e ^{-(y + x/y)}
donde: 0<x<∞ , 0<y<∞ \
a) Verifique que es una función de densidad conjunta
b) Determine las funciones de densidad marginal
c) Encuentre la Covarianza(X, Y)
Rúbrica: literal a y b (7 puntos), literal c (6 puntos)
Tema 2 (25 puntos). Dado el proceso o señal diente de sierra, descrito en la gráfica, con periodo π/3. 
Suponga que X es una variable aleatoria uniforme, distribuida en el intervalo de (0, π].
a) Determine la función densidad de probabilidad para Y
b) Calcule la función de distribución acumulada para Y
c) Grafique su resultado
Rúbrica: literales a y b (10 puntos cada uno), literal c (5 puntos)
Tema 1 (30 puntos). En una ciudad existen 3 cadenas de supermercados (X, Y, Z) y se dispone de la movilidad de los clientes entre ellos. 
En septiembre de un total de 1 millón de clientes, la cuarta parte realiza las compras en el supermercado X, 1/3 va al supermercado Y, mientras que 5/12 adquiere productos en el supermercado Z.
En cada mes el supermercado X retiene el 90% de sus clientes y pierde el 10% que van al supermercado Y.
Se determinó que del supermercado Y solo retiene el 5% de sus clientes y el 85% se cambian a X y el resto va a Z.
El supermercado Z retiene solo el 40% de su clientela, el 50% va al supermercado X y el 10 % se cambia a Y.
a) Determine los estados del problema
b) Realice el diagrama de transición
c) Elabore la matriz de transición correspondiente
d) Clasifique los estados del problema
e) Determine el vector de probabilidad estable
f) ¿Cuál es la proporción de clientes para los supermercados al mes siguiente?
g) Suponga que observa un cliente del supermercado Y:
1. Determine la probabilidad que en el siguiente periodo sea cliente de Z.
2. Luego el cliente del numeral anterior al segundo periodo decida cambiarse a X
3. Para un cliente de Y, determine la probabilidad que luego de tres periodos no termine comprando en X.
Rúbrica: Literales a al f (4 puntos cada uno), literal g (6 puntos).
Tema 5 (10 puntos). Si el proceso estocástico X(t) del tema anterior pasa por un sistema con función de transferencia h(t) 
h(t) = 4 e^{-2t} \mu (t)
a) Determine la densidad espectral de potencia en la salida
b) Calcule la potencia promedio del proceso en la salida
Tema 4 (20 puntos) Asuma un proceso estocástico X(t) estacionario en el sentido amplio con función de auto-correlación
R_x(t) = e^{-|\tau |}, \tau \in \Re
a) Determine la densidad espectral de potencia del proceso A(t) = X(t) − X(t−1)
b) Calcule la potencia promedio del proceso A(t)
Tema 3 (20 puntos). Considere el proceso estocástico estacionario en el sentido amplio X(t) con media cero y con auto-correlación
R_x = 50 \cos (20 \pi \tau) + 18 \cos (30 \pi \tau)
a) Determine Var(X(t))
b) Determine la potencia promedio
c) Calcule la densidad espectral de potencia SX(f)
Tema 2 (25 puntos). Dado el proceso o señal descrito por: 
X(t) = cos(ω t + Φ)
donde Φ es una variable aleatoria uniforme en el intervalo (-π, π)
a) Encuentre la auto-covarianza de X(t).
b) Determinar y si el proceso es estacionario o estacionario en el sentido amplio. Justifique su respuesta
c) Determine si la densidad espectral de potencia SX(f)
Tema 1. (25 puntos). Dado el proceso o señal descrito por: 
Y=cos(X)
Suponga que X es una variable aleatoria uniforme, distribuida en el intervalo de (0, 2π].
a) Determine la función densidad de probabilidad para Y
b) Calcule la función de distribución acumulada para Y
c) Grafique su resultado
Este esquema de modulación es conocido también como Quaternary PSK (PSK Cuaternaria), Quadriphase PSK (PSK Cuadrafásica).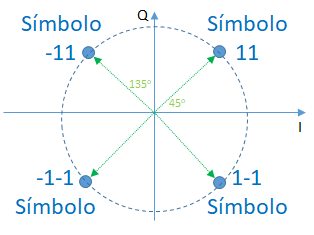 
Esta modulación digital es representada en el diagrama de constelación por cuatro puntos equidistantes del origen de coordenadas.
Con cuatro fases, QPSK puede codificar dos bits por cada símbolo.
Respecto a un ancho de banda predeterminado, la ventaja de QPSK sobre BPSK está que con el primero se transmite el doble de la velocidad de datos en un ancho de banda determinado en comparación con BPSK, usando la misma tasa de error.
En el caso de la canción procesada en BPSK, se cargan una cantidad de datos que se pueden procesar con la mitad de símbolos, enviando la información por pares.
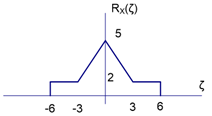
La pmf del proceso QPSK será:
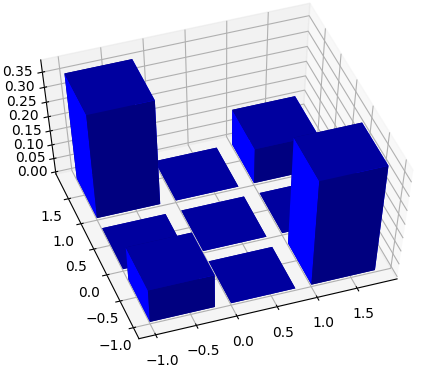
Resultados del algoritmo:
datos cargados: 8595119 símbolos procesados: 4297559 [[ 539083 0 1580668] [ 1 0 0] [1638724 0 539083]] pmf[x,y] [[ 1.25439348e-01 0.00000000e+00 3.67806003e-01] [ 2.32690232e-07 0.00000000e+00 0.00000000e+00] [ 3.81315067e-01 0.00000000e+00 1.25439348e-01]] >>>
# Modulacion digital QPSK - pmf # propuesta:edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt # INGRESO # archivo = input('archivo de delta-sigma:' ) narchivo = 'elaguacate_deltasigma_datos.txt' senal = np.loadtxt(narchivo,dtype=int) # PROCEDIMIENTO n = len(senal) simbolos = [-1,0,1] m = len(simbolos) # Codificar de 2 en dos agrupar = 2 cuenta = np.zeros(shape=(m,m), dtype=int) nmax = (n//agrupar)*agrupar for i in range(0,nmax,agrupar): a = senal[i] b = senal[i+1] f = simbolos.index(a) c = simbolos.index(b) cuenta[f,c] = cuenta[f,c]+1 k = np.sum(cuenta) pxy = cuenta/k # SALIDA print('datos cargados: ', n) print('símbolos procesados: ', k) print(cuenta) print('pmf[x,y]') print(pxy) # Gráfica: from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() ax = fig.add_subplot(111, projection='3d') xpos, ypos = np.meshgrid(simbolos,simbolos) xpos = xpos.flatten('F') ypos = ypos.flatten('F') zpos = np.zeros_like(xpos) dx = 0.8 * np.ones_like(zpos) dy = dx.copy() dz = pxy.flatten() ax.bar3d(xpos, ypos, zpos, dx, dy, dz, color='b', zsort='average') plt.show()
Tarea: Obtener las pmf marginales del ejercicio.