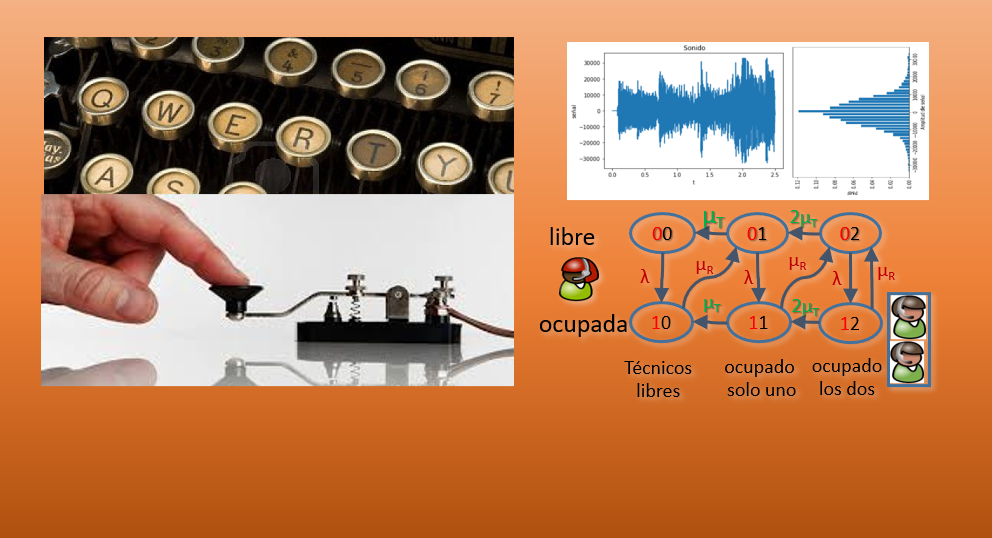
Referencia: León-García 9.6, 9.6.1 p518,521; Gubner 10.3, 10.2 p395, p392; Ross 10.7 p654, p656
Estacionario
Un proceso aleatorio discreto o contínuo en el tiempo X(t) es estacionario si la distribución conjunta de cualquier grupo de muestras No depende de la ubicación del tiempo de origen.F_{X(t_1),..., X(t_k)} (x_1, ... x_k) = F_{X(t_1+\tau),..., X(t_k)} (x_1, ... x_k+\tau)
para cualquier τ, k, o muestras t1, ... , tk.
Estacionario con cdf de 1er Orden
Un proceso aleatorio estacionario con cdf de primer orden debe ser independiente del tiempo
F_{X(t)} (x) = F_{X(t+\tau)} (x) = F_X(x)para todo t, τ, dicho de otra forma, sus resultados son constantes
m_{X}(t) = E[X(t)]=m VAR[X(t)] = E[(X(t)-m)^2] = \sigma ^2Estacionario con cdf de 2do Orden
Un proceso aleatorio estacionario con cdf de segundo orden debe depender solo de la diferencia de tiempo entre muestras y NO en particular del tiempo de las muestras
F_{X(t_1),X(t_2)} (x_1,x_2) = F_{X(0),X(t_2-t_1)} (x_1,x_2)para todo t1, t2
R_{X}(t_1,t_2) = R_{X} (t_2-t_1) C_{X}(t_1,t_2) = C_{X} (t_2-t_1)Estacionario en el Sentido Amplio (WSS o débil)
Un proceso aleatorio discreto o contínuo en el tiempo X(t) es estacionario en el sentido amplio (WSS) si satiface que:m_X(t) = m C_{X}(t_1,t_2) = C_{X} (t_2-t_1)
De forma semejante, los procesos X(t) y Y(t) son estacionarios conjuntos si ambos son estacionarios en el sentido amplio y si covarianza cruzada depende solo de t1-t2.
R_{X}(t_1,t_2) = R_{X} (\tau) C_{X}(t_1,t_2) = C_{X} (\tau)