Publicado en

Aplicaciones

Publicado en

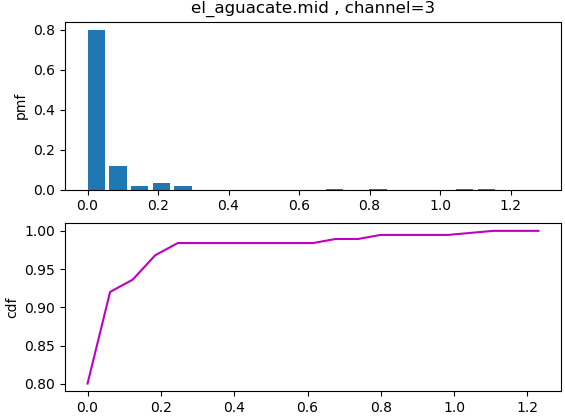
Midi un instrumento, teclas pmf y cdf

Se realiza el conteo de cada tecla de un instrumento para una canción desde un archivo.midi

# Pmf de notas de un instrumento
# desde archivo midi

import numpy as np
import matplotlib.pyplot as plt
import mido as md

# INGRESO
archivomid = 'el_aguacate.mid'
# instrumento
canal = 'channel=3' 
# para pmf
tramos = 100     

# PROCEDIMIENTO
# Abre archivo midi
partitura = md.MidiFile(archivomid)

# un instrumento, tabla de notas
transcurrido = 0
deltat = 0
accion = 'note_on'
tabla = []
for dato in partitura:
    linea = str(dato)
    parte = linea.split(' ')
    if (parte[0]==accion):
        valor = parte[4].split('=')
        tiempo = float(valor[1])
        transcurrido = transcurrido + tiempo
        deltat = deltat+tiempo
        if (parte[1]==canal):
            valor = parte[2].split('=')
            nota = int(valor[1])
            valor = parte[3].split('=')
            velocidad = int(valor[1])
            tabla.append([nota, velocidad, tiempo, deltat])
            deltat=0
tabla = np.array(tabla)
m = len(tabla)

notas = tabla[:,0]
x, cuenta = np.unique(notas, return_counts=True)
print(x)
print(cuenta)

frelativa = cuenta/np.sum(cuenta)
acumulada = np.cumsum(frelativa)
            
deltax = 1

# GRAFICAS
plt.subplot(211)
plt.bar(x,frelativa, width=deltax*0.8, align='edge')
plt.title('notas, '+ archivomid + ' , ' + canal)
plt.ylabel('pmf')

plt.subplot(212)
plt.plot(x,acumulada,'m')
plt.ylabel('cdf')
plt.show()
Publicado en

MIDI un instrumento

Referencias: Wikipedia

MIDI (Musical Instrument Digital Interface) es un protocolo estándar, una interfaz digital y conectores que permiten que varios instrumentos musicales electrónicos, ordenadores y otros dispositivos relacionados se conecten y comuniquen entre sí.

De un archivo MIDI se puede usar las instrucciones para una solo intrumento, por ejemplo el que ejecuta la melodía, y revisar los delta tiempos entre cada nota para encontrar su pmf o cdf.

Archivo ejemplo: el_aguacate.mid

Formato de MIDI

Las intrucciones midi se puden leer usando la librería mido de python.

Para instalar la librería puede usar pip install mido en la uso de una ventana“símbolo de sistema”. Revisar instrucciones en el enlace pip install.

Para abrir el archivo y crear un documento de texto que se pueda interpretar, se dispone del siguiente script de python:

import mido as md

# INGRESO
archivomid = 'el_aguacate.mid'
archivotxt = 'el_aguacatemidi.txt'

# PROCEDIMIENTO
partitura = md.MidiFile(archivomid)

# SALIDA
pistas = partitura.tracks
n = len(pistas)
for i in range(0,n,1):
    print(i, pistas[i])

# ARCHIVO DE TEXTO
archivo = open(archivotxt,'w')
for dato in partitura:
    archivo.write(str(dato) + '\n')
archivo.close()

que muestra el número de pistas/instrumentos en el archivo.mid y crea un archivo de texto.

0 <midi track 'untitled' 47 messages>
1 <midi track 'BAJO' 1041 messages>
2 <midi track 'PIANO' 3079 messages>
3 <midi track 'GUITARRAS' 943 messages>
4 <midi track 'JAZZ GTR' 383 messages>
5 <midi track 'PLATILLO' 1002 messages>
6 <midi track 'TAMBOR' 470 messages>

También se puede procesar los datos, para un instrumento, y utilizar las medidas de tiempo como parámetro para tabular el comportamiento y obtener la pmf y cdf.

import numpy as np
import matplotlib.pyplot as plt
import mido as md

# INGRESO
archivomid = 'el_aguacate.mid'
# instrumento
canal = 'channel=3' 
# para pmf
tramos = 20     

# PROCEDIMIENTO
# Abre archivo midi
partitura = md.MidiFile(archivomid)

# un instrumento, tabla de notas
accion = 'note_on'
tabla = []
for dato in partitura:
    linea = str(dato)
    parte = linea.split(' ')
    if (parte[0]==accion and parte[1]==canal):
        valor = parte[2].split('=')
        nota = int(valor[1])
        valor = parte[3].split('=')
        velocidad = int(valor[1])
        valor = parte[4].split('=')
        tiempo = float(valor[1])
        tabla.append([nota, velocidad, tiempo])
tabla = np.array(tabla)
m = len(tabla)

# Cuenta de tiempos
xmin = 0
xmax = np.round((np.max(tabla[:,2])*1.1),2)
muestreo = tramos +1
x = np.linspace(xmin,xmax,muestreo)
deltax = x[1]-x[0]
cuenta = np.zeros(muestreo,dtype=int)
for f in range(0,m,1):
    valor = tabla[f,2]
    encuentra = 0
    j=0
    while not(j>=muestreo or encuentra==1):
        if x[j]>valor:
            cuenta[j-1] = cuenta[j-1]+1
            encuentra=1
        j=j+1
frelativa = cuenta/np.sum(cuenta)
acumulada = np.cumsum(frelativa)
            
# SALIDA
# Presenta pistas
pistas = partitura.tracks
n = len(pistas)
print('pistas/instrumentos: ')
for i in range(0,n,1):
    print(i, pistas[i])
# Tabulados
print('Tabulados: ')
print('     x: ',x)
print('cuenta: ', cuenta)

# GRAFICAS
plt.subplot(211)
plt.bar(x,frelativa, width=deltax*0.8, align='edge')
plt.title(archivomid + ' , ' + canal)
plt.ylabel('pmf')

plt.subplot(212)
plt.plot(x,acumulada,'m')
plt.ylabel('cdf')
plt.show()

Tarea:

a) Descargar el archivo.mid de la canción de su preferencia, seleccionar una pista y procesar las funciones de probabilidad de masas y acumulada.

b) para las notas del instrumento, mostrar tambien la pmf, cdf

Ejemplo de instrucciones midi generadas en el archivo

control_change channel=9 control=7 value=120 time=0
note_on channel=2 note=62 velocity=64 time=1.5
note_on channel=2 note=58 velocity=64 time=0
note_on channel=2 note=58 velocity=0 time=0.155
note_on channel=2 note=62 velocity=0 time=0.08
note_on channel=0 note=43 velocity=64 time=0.065
note_on channel=1 note=74 velocity=64 time=0
note_on channel=1 note=70 velocity=64 time=0
note_on channel=1 note=62 velocity=64 time=0
note_on channel=2 note=70 velocity=64 time=0
note_on channel=2 note=67 velocity=64 time=0
note_on channel=9 note=46 velocity=64 time=0
note_on channel=9 note=46 velocity=0 time=0.07
Publicado en

PAM a PSK media cuadrática derivable

Y(t) = a \cos \big( 2\pi t + \frac{\pi}{2}X(t) \big) R_y(t_1,t_2) = E[Y(t_1)Y(t_2)] = a^2 \sin (2\pi t_1) \sin(2\pi t_2)

f) ¿Y(t) tiene media cruadrática derivable? Si lo es, encuentre las funciones para media y autocorrelacón.

Y(t) es diferenciable entodos los puntos

\frac{\delta y}{\delta t}Y(t) = \frac{\delta y}{\delta t} \big[ a \cos \big( 2\pi t + \frac{\pi}{2}X(t) \big)\big] = a(-2\pi) \sin \big( 2\pi t + \frac{\pi}{2}X \big) \big]

media o valor esperado:

E \big[ \frac{\delta y}{\delta t}Y(t) \big] = \frac{\delta y}{\delta t} E[Y(t)] = 0

autocorrelación:

R_{Y'}(t_1, t_2) = \frac{\delta ^2}{\delta t_1 \delta t_2} R_Y((t_1, t_2) = \frac{\delta ^2}{\delta t_1 \delta t_2} \big[a^2 \sin (2\pi t_1) \sin(2\pi t_2)\big] = a^2(2\pi ) \cos(2\pi t_1) \frac{\delta }{ \delta t_2} \big[\sin(2\pi t_2)\big] = a^2 (2\pi) \cos (2\pi t_1)(2\pi) \sin (2\pi t_2) = 4 \pi^2 a^2 \cos(2\pi t_1) \sin(2\pi t_2)

para nT ≤ t1 , t2 < (n+1)T

0 para otro caso

 

Publicado en

PAM a PSK media cuadrática contínua

R_y(t_1,t_2) = E[Y(t_1)Y(t_2)] = a^2 \sin (2\pi t_1) \sin(2\pi t_2)

e) ¿El proceso Y(t) tiene media cuadrática contínua?

Sí, por las condiciones siguientes:

Referencia: León-García 9.7.1 p.531

Si RX(t1,t2) es contínua en t1 y t2 en el punto (t0,t0), entonces X(t) tiene media cuadrática continua en t0.

Si X(t) tiene media cuadrática contínua en t0 , entonces la función media mX(t) debe ser contínua en t0.

Si RX(τ) es contínua en τ=0 entondes el proceso estocástico estacionario en el sentido amplio WSS para X(t) es contino en la media cuadtática en todos los  puntos t0.

Publicado en

PAM a PSK determinar estacionario

Los resultados son:

E[Y(t)] = 0 R_y(t_1,t_2) = E[Y(t_1)Y(t_2)] = a^2 \sin (2\pi t_1) \sin(2\pi t_2) C_{Y} (t_1,t_2) = E[Y(t_1)Y(t_2)] + E[Y(t_1)]E[Y(t_2)] = a^2 \sin (2\pi t_1) \sin(2\pi t_2) + 0 = a^2 \sin (2\pi t_1) \sin(2\pi t_2)

siendo la media una constante = 0, entonces:

C_Y[t_1, t_2] = R_y(t_1,t_2) C_Y[t_1, t_2] = a^2 \sin (2\pi t_1) \sin(2\pi t_2)

Existe un valor T tal que:

C_Y[t_1, t_2] = C_Y[t_1 + mT, t_2 + mT]

El proceso es clasificado como ciclo-estacionario

para:

para nT ≤ t1 , t2 < (n+1)T

0 para otro caso

Publicado en

PAM a PSK autocorrelación

Y(t) = a \cos \big( 2\pi t + \frac{\pi}{2}X(t) \big)

c) Encuentre la media y autocorrelacion de Y(t)

E[Y(t_1) Y(t_2)] = E\big[a \cos \big( 2\pi t_1 + \frac{\pi}{2}X \big) . a \cos \big( 2\pi t_2 + \frac{\pi}{2}X\big)\big] g(x) = a \cos \big( 2\pi t_1 + \frac{\pi}{2}X \big) . a \cos \big( 2\pi t_2 + \frac{\pi}{2}X\big)

Referencia: Valor esperado de funciones de variable aleatoria (León-García 3.3.1 p. 107
Si z =g(x)
E[g(x)] = \sum_k g(x_k)p_x(X_k)
tomando la pmd mostrada en el cálculo del valor esperado, se tiene entonces que:
= \big[ a \cos \big( 2\pi t_1 + \frac{\pi}{2}(-1)\big) . a \cos \big( 2\pi t_2 + \frac{\pi}{2}(-1)\big)\big] \frac{1}{2} +
+ \big[ a \cos \big( 2\pi t_1 + \frac{\pi}{2}(1)\big) . a \cos \big( 2\pi t_2 + \frac{\pi}{2}(1)\big)\big] \frac{1}{2}
= \frac{a^2}{2} \cos \big( 2\pi t_1 - \frac{\pi}{2}\big) \cos \big( 2\pi t_2 - \frac{\pi}{2}\big) +
+ \frac{a^2}{2}\cos \big( 2\pi t_1 + \frac{\pi}{2}\big) \cos \big( 2\pi t_2 + \frac{\pi}{2}\big)
= \frac{a^2}{2} \sin (2\pi t_1) \sin (2\pi t_2) +
+ \frac{a^2}{2}[-\sin(2\pi t_1)][-\sin (2\pi t_2)]
= \frac{a^2}{2} 2 \sin (2\pi t_1) \sin( 2\pi t_2)
= a^2 \sin ( 2\pi t_1) \sin(2\pi t_2)
= \frac{a^2}{2}\big[ \cos(2\pi t_1 - 2\pi t_2) - \cos(2\pi t_1 + 2\pi t_2) \big]
E[Y(t_1)Y(t_2)] = \frac{a^2}{2}\big[ \cos(2\pi t_1 - 2\pi t_2) - \cos(2\pi t_1 + 2\pi t_2) \big]

Publicado en

PAM a PSK – valor esperado

Y(t) = a \cos \big( 2\pi t + \frac{\pi}{2}X(t) \big)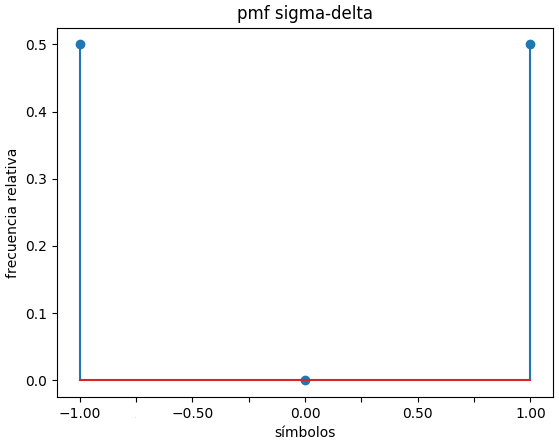

La pmf de x(t) es 0.5 para cada valor de [-1,1]

c) Encuentre la media y autocorrelación de Y(t)

E[Y(t)] = E\big[ a \cos \big( 2\pi t + \frac{\pi}{2}X \big)\big]

Referencia:  León-García 3.3.1 p. 107. Valor esperado de funciones de variable aleatoria

Si z =g(x)

E[g(x)] = \sum_k g(x_k)p_x(X_k)

se tiene entonces que:

= \big[a \cos \big( 2\pi t + \frac{\pi}{2}(-1) \big)\big]\frac{1}{2} + \big[a \cos \big( 2\pi t + \frac{\pi}{2}(1) \big)\big] \frac{1}{2} = \frac{a}{2}\cos \big( 2\pi t - \frac{\pi}{2} \big) + \frac{a}{2}\cos \big( 2\pi t + \frac{\pi}{2} \big) = \frac{a}{2} \sin \big( 2\pi t \big) - \frac{a}{2} \sin \big( 2\pi t \big) = 0 E[Y(t)] = 0