Categoría: Alfabeto-Texto

Referencia: Teclado Qwerty Wikipedia

Uso del teclado QWERTY

El nombre del teclado QWERTY proviene de las primeras seis letras de su fila superior, fue diseñado y patentado por Christopher Sholes en 1868 y vendido a Remington en 1873.

La distribución QWERTY se diseñó con objetivo de separar las letras más usadas de la zona central del teclado, para evitar que se atascaran las máquinas de escribir de primera generación. Actualmente, ésta propiedad no es más requerida, sin embargo se ha heredado la distribución en los teclados de computadora.

A partir de la frecuencia de uso de las letras del alfabeto, se requiere conocer la frecuencia de uso de cada fila del teclado. Los valores de frecuencia para cada letra se encuentran en el archivo: usoletras.txt que por cada línea registra la letra y frecuencia relativa separadas por una coma ‘,’.

archivo: usoletras.txt:
a, 0.11422682511 
b, 0.0118959769969 
c, 0.0464006717728 
d, 0.0543525280541 
...

Algoritmo en Python

# Analiza teclado QWERTY
# Datos desde Archivo 'usoletras.txt'
import numpy as np

# Ingreso
narchivo = input('Nombre del archivo:')
veces    = []
archivo  = open(narchivo,'r')
linea    = archivo.readline()
while not(linea == ''):
    partes = linea.split(',')
    letra  = partes[0]
    frecuencia = float(partes[1])
    veces.append([letra,frecuencia])
    linea = archivo.readline()
archivo.close()

# PROCEDIMIENTO
superior = 'qwertyuiop'
media    = 'asdfghjklñ'
inferior = 'zxcvbnm'
k = len(veces)
usofila = np.zeros(3,dtype=float)
for i in range(0,len(veces),1):
    if (veces[i][0] in superior):
        usofila[0] = usofila[0]+veces[i][1]
    if (veces[i][0] in media):
        usofila[1] = usofila[1]+veces[i][1]
    if (veces[i][0] in inferior):
        usofila[2] = usofila[2]+veces[i][1]

# SALIDA
print(usofila)

resultado:

[ 0.48999975  0.32815084  0.18184941]

La gráfica para pmf se obtiene al añadir las instrucciones:

# GRAFICA
% matplotlib inline
import matplotlib.pyplot as plt
plt.stem([0,1,2],usofila)
plt.title('PMF filas teclado QWERTY')
plt.xlabel('fila superior, media e inferior')
plt.show()

Tarea: En cada caso, realice la gráfica de funciones de probabilidad de masa (pmf) y la función de probabilidades acumulada (cdf)

• Encuentre la frecuencia de uso de cada mano, presente la división propuesta de el teclado en dos partes: izquierda y derecha.
• Realice el ejercicio para determinar la frecuencia de uso de cada dedo de cada mano. Presente un modelo gráfico de cada tecla, para mostrar de mejor forma la medida a obtener
• con los resultados de éste ejercicio, considere llenar la siguiente tabla:
  

  	mano izquierda	mano derecha	total fila
  superior
  media
  inferior
  total mano

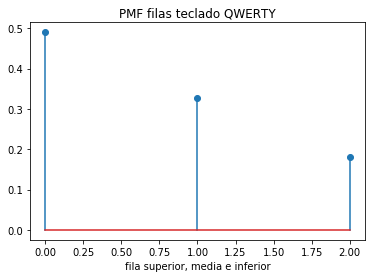
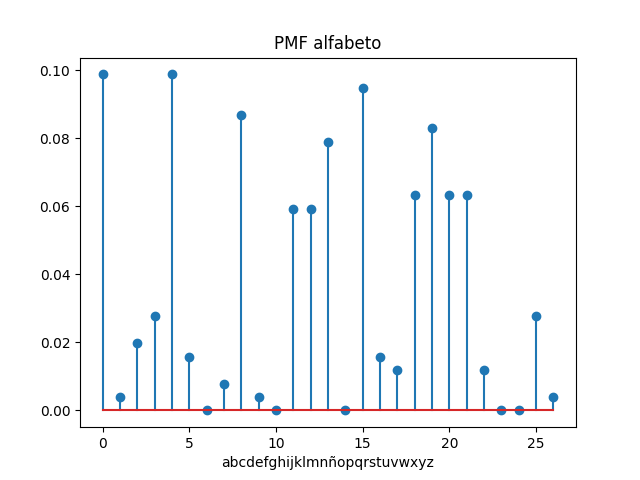
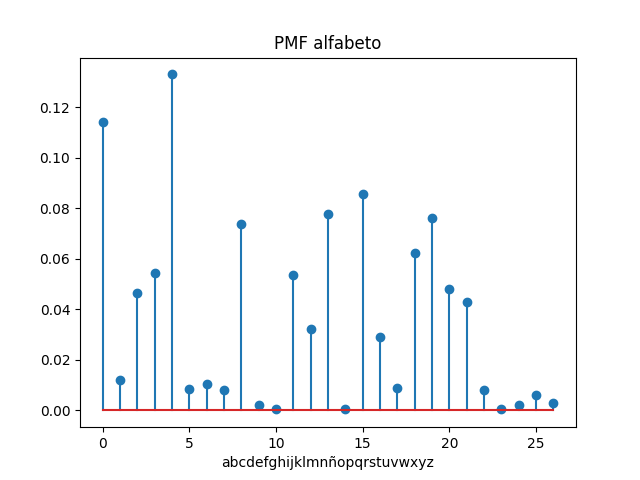
Referencia: Ross 2.2 p25, Telex, TTY o teletipo(Wikipedia)

Funciones de probabilidad de masa para alfabeto

Para el «TELEX», «TTY», «teletype» o sistema de tranmisión/recepción de mensajes de texto mecanografiados, al desconocer el contenido del mensaje se podría considerar que cada letra presenta un comportamiento aleatorio. Se puede intuir que hay letras que son poco comunes como ‘x’ y otras muy comunes como ‘e’.

Para el modelo se requiere estimar función de probabilidad de masa (pmf), tomando como base solo el alfabeto incluyendo la letra ‘ñ’, sin discriminar mayúsculas y minúsculas.

Para un ensayo, se usaría un texto con una cantidad considerable de letras, como por ejemplo una obra literaria.

Por ejemplo: ‘elaguacate_Letra.txt‘

Referencia: https://achiras.net.ec/el-aguacate-un-pasillo-ecuatoriano-sin-tiempo/

Para procesar el texto se usa como entrada un archivo en formato .txt, analizando por línea, por símbolo y contando las veces que aparece cada letra del alfabeto. La frecuencia relativa de cada letra respecto al total de letras, permitirá visualizar la forma de la función probabilidad de masa (pmf) para el alfabeto.

Nota: Considere solo el total de letras, no el total de símbolos (no incluye «,;.!?» etc.)

Algoritmo en Python

# procesar un archivo de texto
# Determinar la función de probabilidad de masa
# para las letras del alfabeto(incluye ñ)
import numpy as np

# INGRESO
# archivo=input('archivo a leer.txt: ')
nombrearchivo='elaguacate_Letra.txt'

# PROCEDIMIENTO
alfabeto='abcdefghijklmnñopqrstuvwxyz'
k=len(alfabeto)
veces=np.zeros(k,dtype=int)
total=0
# procesa el archivo
archivo = open(nombrearchivo,'r')
unalinea = archivo.readline()
while not(unalinea==''):
    n=len(unalinea)
    unalinea = unalinea.strip('\n')
    unalinea = unalinea.lower()
    m=len(unalinea)
    for j in range(0,m,1):
        unsimbolo=unalinea[j]
        donde = alfabeto.find(unsimbolo)
        if (donde>=0): #Si no encuentra es negativo
            veces[donde]=veces[donde]+1
            total=total+1
    unalinea = archivo.readline()
archivo.close()

frelativa=veces/total
alfa=np.arange(0,len(alfabeto))

# SALIDA
print('Letras contadas: ', total)
print('i,letra,veces,frelativa')
for i in range(0,len(alfabeto),1):
    print(i, alfabeto[i],veces[i], frelativa[i])

el resultado obtenido es:

Letras contadas:  253
i,letra,veces,frelativa
0 a 25 0.098814229249
1 b 1 0.00395256916996
2 c 5 0.0197628458498
3 d 7 0.0276679841897
4 e 25 0.098814229249
5 f 4 0.0158102766798
6 g 0 0.0
7 h 2 0.00790513833992
8 i 22 0.0869565217391
9 j 1 0.00395256916996
10 k 0 0.0
11 l 15 0.0592885375494
12 m 15 0.0592885375494
13 n 20 0.0790513833992
14 ñ 0 0.0
15 o 24 0.0948616600791
16 p 4 0.0158102766798
17 q 3 0.0118577075099
18 r 16 0.0632411067194
19 s 21 0.0830039525692
20 t 16 0.0632411067194
21 u 16 0.0632411067194
22 v 3 0.0118577075099
23 w 0 0.0
24 x 0 0.0
25 y 7 0.0276679841897
26 z 1 0.00395256916996

para la gráfica se añade al algoritmo:

# GRAFICA
% matplotlib inline
import matplotlib.pyplot as plt
plt.stem(alfa,frelativa)
plt.title('PMF alfabeto')
plt.xlabel(alfabeto)
plt.show()

---

otro experimento realizado con:
Poe, Edgar Allan. Eureka. Vol. 13. EDAF, 2006.

tiene el siguiente resultado:

Letras contadas:  78598
i,letra,veces,frelativa
0 a 8978 0.11422682511
1 b 935 0.0118959769969
2 c 3647 0.0464006717728
3 d 4272 0.0543525280541
4 e 10455 0.133018651874
5 f 658 0.00837171429298
6 g 818 0.010407389501
7 h 632 0.00804091707168
8 i 5792 0.0736914425303
9 j 161 0.00204839817807
10 k 36 0.000458026921805
11 l 4203 0.0534746431207
12 m 2541 0.0323290668974
13 n 6126 0.0779409145271
14 ñ 46 0.000585256622306
15 o 6725 0.0855619735871
16 p 2271 0.0288938649838
17 q 692 0.00880429527469
18 r 4899 0.0623298302756
19 s 5988 0.0761851446602
20 t 3792 0.0482455024301
21 u 3362 0.0427746253085
22 v 647 0.00823176162243
23 w 34 0.000432580981704
24 x 177 0.00225196569887
25 y 491 0.00624697829461
26 z 220 0.00279905341103

Será necesario que realizar el experimento muchas veces para tener un comportamiento más general, se propone realizar al estudiante su experimento con otros textos.

Con los resultados, se requiere:

1. Realizar la pmf para vocales
2. Realizar la pmf para consonantes
3. determine las letras con menor probabilidad de cada grupo
4. escriba alguna recomendación para mejorar el experimento
5. escriba al menos una conlusión

Considere lo siguiente:

Si en una transmisión de texto, por ruido en el canal se cambian aleatoriamente algunos caracteres,

• ¿Cuáles cambios serían los que afectan menos al mensaje?
• ¿Cuáles cambios serían los que afectan más al mensaje?

---

En caso de presentar el resultado de frecuencias relativas en un archivo:

# Archivo
narchivo='usoletras.txt'
archivo=open(narchivo,'w')
for i in range(0,k,1):
    linea=alfabeto[i]+','+str(frelativa[i])+'\n'
    archivo.write(linea)
archivo.close()