Para la transmisión de texto, por ejemplo la letra de una canción, se puede codificar a Morse usando inicialmente el procedo de los ejemplos anteriores.
Por ejemplo, una parte del archivo origen: elaguacate_Letra.txt
Tu eres mi amor
mi dicha y mi tesoro
mi sólo encanto
y mi ilusión.
se convertiría en: elaguacate_morse.txt
- ..- . .-. . ... -- .. .- -- --- .-.
-- .. -.. .. -.-. .... .- -.-- -- .. - . ... --- .-. ---
-- .. ... --- .-.. --- . -. -.-. .- -. - ---
-.-- -- .. .. .-.. ..- ... .. --- -. .-.-.-
que puede ser guardado en otro archivo y procesado como un proceso estocástico.
Hay que considerar que en la codificación estandar Morse, no existen las letras con tíldes ('áéíóú') que para la transmisión se debe quitar las tildes.
Funciones complementarias
Se usa como función básica como codificador Morse la descrita en el problema básico.
Cuando el tema a tratar es un texto más largo, se abordan más detalles del procesamiento del texto, como el quitar las tildes antes de codificar la letra. En el estándar de la codificación Morse (origen en inglés) no se usaban las tildes en las letras, para ésta operación se usa la funcion quitatildes().
Como complemento se añaden las funciones de codificación por línea, otra función para el conteo de símbolos,
La codificación en python usada para el ejemplo se adjunta:
# Código Morse - codificador de texto
# propuesta: edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
def morsecodec(caracter):
equivale={
'A':'.-', 'B':'-...', 'C':'-.-.',
'CH':'----', 'D':'-..', 'E':'.',
'F':'..-.', 'G':'--.', 'H':'....',
'I':'..', 'J':'.---', 'K':'-.-',
'L':'.-..', 'M':'--', 'N':'-.',
'Ñ':'--.--', 'O':'---', 'P':'.--.',
'Q':'--.-', 'R':'.-.', 'S':'...',
'T':'-', 'U':'..-', 'V':'...-',
'W':'.--', 'X':'-..-', 'Y':'-.--',
'Z':'--..',
'0':'-----', '1':'.----', '2':'..---',
'3':'...--', '4':'....-', '5':'.....',
'6':'-....', '7':'--...', '8':'---..',
'9':'----.',
'.':'.-.-.-', ',':'-.-.--', '?':'..--..',
'"':'.-..-.', '!':'--..--', ' ':' '}
# Si caracter no está en equivale
codigo = caracter
# codifica a morse
caracter = caracter.upper()
if (caracter in equivale):
codigo = equivale[caracter]
return(codigo)
def quitatildes(linea):
sintilde = {'á':'a', 'é':'e', 'í':'i',
'ó':'o', 'ú':'u'}
nueva = ''
for caracter in linea:
if (caracter in sintilde):
caracter = sintilde[caracter]
nueva = nueva + caracter
return(nueva)
def morselinea(linea):
linea = linea.strip('\n')
linea = linea.strip(' ')
linea = quitatildes(linea)
lineamorse = ''
for caracter in linea:
enmorse = morsecodec(caracter)
lineamorse = lineamorse + enmorse + ' '
return(lineamorse)
def cuentasimbolo(texto,simbolos):
k = len(simbolos)
veces = np.zeros(k,dtype=int)
n = len(texto)
for fila in range(0,n,1):
unalinea = texto[fila]
unalinea = unalinea.strip('\n')
m = len(unalinea)
for caracter in unalinea:
donde = simbolos.find(caracter)
if (donde>=0): #Si no encuentra es negativo
veces[donde] = veces[donde]+1
total = np.sum(veces)
return(veces)
# PROGRAMA -----------------------------
# INGRESO
nombrearchivo = 'elaguacate_Letra.txt'
# PROCEDIMIENTO
# procesa el archivo
archivo = open(nombrearchivo,'r')
unalinea = archivo.readline()
codificado = []
while not(unalinea==''):
unalinea = unalinea.strip('\n')
unalinea = unalinea.lower()
lineamorse = morselinea(unalinea)
codificado.append(lineamorse)
unalinea = archivo.readline()
archivo.close()
# cuenta símbolos
simbolos = '.- '
conteo = cuentasimbolo(codificado,simbolos)
total = np.sum(conteo)
pmf = conteo/total
# SALIDA
print('Texto en morse: ')
n = len(codificado)
etiquetas = ['punto','raya','espacio']
for i in range(0,n,1):
print(codificado[i])
# PMF
print('PMF')
print(etiquetas)
print(pmf)
# GRAFICA
x = np.arange(0,len(conteo),1)
plt.stem(x,pmf)
plt.xticks(x,etiquetas)
plt.title('pmf')
plt.show()
# ARCHIVO
narchivo = 'morsetexto.txt'
archivo = open(narchivo,'w')
for i in range(0,n,1):
linea = codificado[i]+'\n'
archivo.write(linea)
archivo.close()
Al final se presenta la pmf, sus valores y gráficas, junto al archivo morsetexto.txt como resultado.
PMF
['punto', 'raya', 'espacio']
[ 0.3588785 0.2953271 0.34579439]

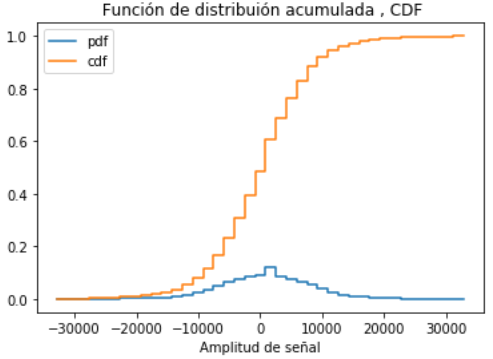
Tarea: Procese los datos necesarios para generar la función de distribución acumulada (cdf), el valor esperado, varianza y desviación estándar.
Realice las observaciones y recomendaciones necesarias para mejorar el algoritmo que haya encontrado al usar su propio texto.