Publicado en

1Eva_IIT2017_T3 Multiplexor-Colas

1ra Evaluación II Término 2017-2018. Noviembre 28, 2017

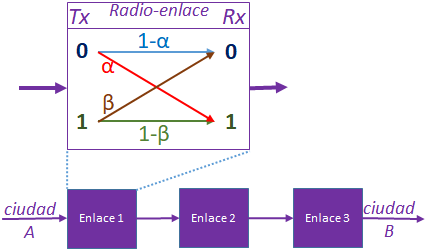
Tema 3. (15 puntos) En telecomunicaciones, la multiplexación permite transmitir varias comunicaciones de forma simultánea combinando dos o más comunicaciones en la entrada y entregando un solo canal/ medio de salida.

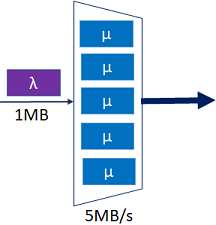Para transmisión de datos se dispone de un multiplexor con capacidad de 5 MB/s que sirve a conexiones que llegan acorde a un proceso Poisson con tasa λ y ocupan 1Mb del ancho de banda del enlace con un tiempo de uso exponencialmente distribuido con parámetro µ.

a) Determine el espacio de estados del sistema

b) Dibuje y etiquete el diagrama de estados del sistema

c) Calcule las probabilidades de cada estado (PMF)

d) Encuentre la probabilidad de pérdidas de conexiones.

e) ¿Cuál es el factor de utilización del enlace?

Rúbrica: literal a y b (5 puntos), literal c (8 puntos), literal d y e (2 puntos)

Referencia: Erlang’s loss System. Ross 8.9.1. p.563, M/M/c/c Queueing System. León-García 12.4.3

Publicado en

1Eva_IIT2017_T2 Radio-enlaces con Markov

1ra Evaluación II Término 2017-2018. Noviembre 28, 2017

Tema 2. (35 puntos) Para comunicar dos ciudades se instalan tres radio-enlaces digitales de larga distancia, cada uno conformado por un transmisor (Tx) y un receptor (Rx). Por ejemplo, las ciudades Guayaquil en la costa y Cuenca en la sierra, se comunican usando tres radio-enlaces que en puntos por tramos en las montañas.

En un radio-enlace el dígito binario 0 enviado por Tx se recibe en Rx con una probabilidad de error α, mientras que el dígito binario 1 presenta probabilidad de error β.

Para un radio-enlace realice un modelo con una Cadena de Markov:

a) Determine el espacio de estados

b) Realice el diagrama de estados, etiquete claramente

c) Escriba la matriz de transición y calcule la probabilidad de estado estable.

Suponga que α=0.01, β=0.02 y determine para todo el enlace entre las ciudades:

d) La matriz de transición entre las ciudades A y B
e) Probabilidad de error para un dígito binario 0 (bit)
f) Probabilidad de error para un bit con valor 1 (bit)
g) El error al transmitir un bit en todo el enlace
h) Observe y comente sus resultados.

Rúbrica: literal a y b (6 puntos), literal c (4 puntos), literal d (10 puntos), literal e y f (3 puntos c/u) literal g (4 puntos), literal h (5 puntos)

Referencia: Gubner(2006) problema 1.56, 3.28, ejemplo 3.13; León-García(2008) 1.5.1; FIEC03236-1ra Evaluación II Término 2011.

Publicado en

1Eva_IIT2017_T1 Código Morse con Markov

1ra Evaluación II Término 2017-2018. Noviembre 28, 2017

Tema 1. (15 puntos) El código Morse fué muy usado en telegrafía, transmisiones por radio marítimas y aéreas. Conocido también como alfabeto Morse, cambia los caracteres alfanuméricos a códigos combinando puntos '.' y rayas '-'.
La separación entre códigos morse se realiza con un espacio ' ', mientras que en la separación entre palabras se usan 3 espacios '   '.

Ejemplo:
un mensaje: ESPOL impulsando la sociedad del conocimiento
. ... .--. --- .-..   .. -- .--. ..- .-.. ... .- -. -.. ---   .-.. .-   ... --- -.-. .. . -.. .- -..   -.. . .-..   -.-. --- -. --- -.-. .. -- .. . -. - ---

Realice un modelo en cadena de Markov para un experimento realizado sobre un texto codificado en morse.

Use como referencia los símbolos = '.- ', en el experimento se contaron los cambios entre símbolos mostrado los valores resultantes en la matriz “conteo”.

a) Determine el espacio de estados
b) Realice el diagrama de estados
c) Escriba la matriz de transición y ubique los valores encontrados en el diagrama.
d) Calcule la probabilidad de estado estable o largo plazo.

conteo = 
[[36532, 35233, 51578],
 [36982, 23931, 30807],
 [49822, 32564, 32194]]

Referencia: http://blog.espol.edu.ec/estg1003/morse-codificador-texto/
Rúbrica: literal a y b (5 puntos), literal c (5 puntos), literal d (5 puntos)

Publicado en

3Eva_IIIT2012_T6 potencia media

3ra Evaluación III Término 2012-2013. Abril 19, 2013. FIEC03236

Tema 6 (20 puntos). Sea X(t) un proceso normal y estacionario, con media 0 y densidad espectral:
S_X = \frac{2}{4 + \omega ^2}
Y sea Y(t) la respuesta de un sistema lineal a la entrada X(t), siendo:
H(\omega) = \begin{cases} 2 && |\omega | \leq 2 \\ 0 && | \omega | \geq 2 \end{cases}
la función de transferencia del sistema.

Calcular:

a) La P[X(t+1)-X(t)>1]
b) La potencia media de X(t) y de Y(t)
c) La P[Y(t)<1]

Rúbrica: literal a y c (6 puntos), literal b (8 puntos)

Publicado en

3Eva_IIIT2012_T5 matriz de covarianza

3ra Evaluación III Término 2012-2013. Abril 19, 2013. FIEC03236

Tema 5 (20 puntos). Un proceso estocástico estacionario X(t) tiene media E[X(t)] = 0 y autocorrelación:

R_{X} (\tau) = 4 e^{-3| \tau |} , \tau \in \Re

a) Calcular la P[X(1)>1]. (4 puntos)

b) Calcular la matriz de covarianza de la v.a. [X(1),X(2),X(3)-X(1)]. (8 puntos)

c) Calcular la P[X(3)-X(1)>1/X(2)>1]. (8 puntos)

Publicado en

3Eva_IIIT2012_T4 funcion densidad bivariada

3ra Evaluación III Término 2012-2013. Abril 19, 2013. FIEC03236

Tema 4 (20 puntos). Las variables aleatorias X e Y son N(1,1) con distribución conjunta normal bidimensional, con coeficiente de correlación

\rho =\frac{1}{2}
Determinar:
a)   La función de densidad de la variable aleatoria: (14 puntos)

U = 2Y – X – 8

b)   P(U>-8). (6 puntos).

Publicado en

3Eva_IIIT2012_T2 Probabilidad de error

3ra Evaluación III Término 2012-2013. Abril 19, 2013. FIEC03236

Tema 2 (20 puntos) Una fuente binaria emite los símbolos -1 y 1 con igual probabilidad.

Cuando se envía  -1, el receptor recibe Z=-1+N, donde N (ruido) es uniforme en (-2,2).

Análogamente cuando se envía 1. Si Z>0, el receptor decide que se envió 1 y si Z<0, que envió -1.

Determine la probabilidad de error.

Publicado en

3Eva_IIIT2012_T1 función densidad

3ra Evaluación III Término 2012-2013. Abril 19, 2013. FIEC03236

Tema 1 (10 puntos). Sea X una variable aleatoria con función de distribución ,

F_X(x) = (1- e^{-\alpha x}) \mu (x-a)

donde α ∈ Re, μ(x) es la función escalón y a ∈ Re+.

Determine:

a)   El valor de α.

b)   P(X=a)

Rúbrica: literal a y b (5 puntos)

Publicado en

2Eva_IIIT2012_T3 autocovarianza

2da Evaluación III Término 2012-2013. Marzo 20, 2013. FIEC03236

Tema 3 (40 puntos). Dada la figura, asuma que el proceso es estocástico:

Siendo X(t) = A*g(t),  donde A es una variable aleatoria que toma los valores -1 y +1 con igual probabilidad, determine:

a) La función (pmf) probabilidad de masa de X(t)

b) E[X(t)], Var[X(t)]

c) La pmf conjunta de X(t) y X(t+d)

d) La CX(t, t+d), d>0

Rúbrica: cada literal (10 puntos)