Publicado en

2Eva_IIT2010_T4 Densidad espectral de potencia

2da Evaluación II Término 2010-2011. Febrero, 2011. FIEC03236

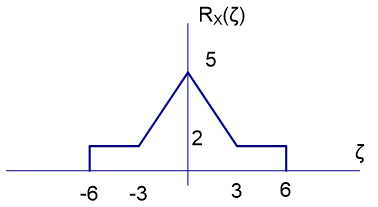
Tema 4 (30 puntos). Asuma un proceso estocástico estacionario en el sentido amplio X(t) con función de autocorrelación:

R_X(t) = 16 + e^{-|t|} , t \in \Re Y(t) = 2 + X(t) cos (12\pi t)

a) Calcule la potencia promedio de X(t)
b) Determine la funcion de autocorrelación RY(t, t+τ)
c) Determine la densidad espectral de potencia Y(t)

Pares de transformadas de Fourier

x(t) \leftrightarrow X(\omega) e^{-a|t|} \leftrightarrow \frac{2a}{a^2 + \omega ^2} , a>0
Publicado en

2Eva_IIT2010_T3 Estacionario en sentido amplio

2da Evaluación II Término 2010-2011. Febrero, 2011. FIEC03236

Tema 3 (20 puntos). Se define un proceso estocástico:

X(t) = A cos(\omega t)+ B sen(\omega t)

donde A y B son variables aleatorias gausianas independientes e identicamente distribuidas (iid) con valores esperados iguales a cero y varianza σ2 .

Determine si X(t) es estacionario en el sentido amplio. Demuestre explícitamente su respuesta.

Publicado en

2Eva_IIT2010_T2 Autocorrelación

2da Evaluación II Término 2010-2011. Febrero, 2011. FIEC03236

Tema 2 (30 puntos). Asuma que X(t) = At +B es un proceso estocástico.
A y B son variables aleatorias independientes que tienen ambas la misma función de densidad uniforme en [-1,1].

Determine:

a) El valor esperado E[X(t)] y autocorrelación RX(t,t+τ)
b) la función de densidad fX(x) de la variable aleatoria de X(1)
c) ¿Existe un valor de t1 y t2 para los cuales X(t1) y X(t2) son variables aleatorias independientes? demuestre su respuesta

Publicado en

2Eva_IIT2010_T1 Limite central

2da Evaluación II Término 2010-2011. Febrero, 2011. FIEC03236

Tema 1 (20 puntos). En un proceso de entrega de paquetes, se cometen errores en la entrega con una probabilidad de 0.15.

Use el terorema del límite central para determinar la probabilidad de que existan 20 o menos errores en 100 entregas

Q(x) = \frac{1}{\sqrt{2 \pi}} \int_{x}^{\infty} e^{-t^2 /2} dt
x Q(x) x Q(x)
0 5.00E-01 2.7 3.47E-03
0.1 4.60E-01 2.8 2.56E-03
0.2 4.21E-01 2.9 1.87E-03
0.3 3.82E-01 3.0 1.35E-03
0.4 3.45E-01 3.1 9.68E-04
0.5 3.09E-01 3.2 6.87E-04
0.6 2.74E-01 3.3 4.83E-04
0.7 2.42E-01 3.4 3.37E-04
0.8 2.12E-01 3.5 2.33E-04
0.9 1.84E-01 3.6 1.59E-04
1.0 1.59E-01 3.7 1.08E-04
1.1 1.36E-01 3.8 7.24E-05
1.2 1.15E-01 3.9 4.81E-05
1.3 9.68E-02 4.0 3.17E-05
1.4 8.08E-02 4.5 3.40E-06
1.5 6.68E-02 5.0 2.87E-07
1.6 5.48E-02 5.5 1.90E-08
1.7 4.46E-02 6.0 9.87E-10
1.8 3.59E-02 6.5 4.02E-11
1.9 2.87E-02 7.0 1.28E-12
2.0 2.28E-02 7.5 3.19E-14
2.1 1.79E-02 8.0 6.22E-16
2.2 1.39E-02 8.5 9.48E-18
2.3 1.07E-02 9.0 1.13E-19
2.4 8.20E-03 9.5 1.05E-21
2.5 6.21E-03 10.0 7.62E-24
2.6 4.66E-03
Publicado en

1Eva_IIT2010_T4 Función densidad

1ra Evaluación II Término 2010-2011. Diciembre, 2010. FIEC03236

Tema 4 (25 puntos). Sean dos variables aleatorias X, Y independientes entre si con distribución gausiana con parámetros

E[X] = 2
Var[X] = 2
E[Y] = 0
Var[Y] = 1

Se define la variable Z=X+Y.
Determine la función de densidad de probabilidad fZ(z).

Publicado en

1Eva_IIT2010_T3 Varianza y Covarianza

1ra Evaluación II Término 2010-2011. Diciembre, 2010. FIEC03236

Tema 3 (25 puntos) En una rifa se sacan números aleatorios de dos tómbolas separadas, donde los números posibles de cada tómbola son:

  • tómbola A: -1, 0 y 1
  • tómbola B: 1,2,3

Sea i el número que se obtiene en la tómbola A y k el de la tómbola B.

Si se definen las variables aleatorias X=|i-k| y Y=i+k, determine

a) P[X  ≤ 2]
b) Dibuje la fY(Y |x=1)
c) Var(X |y=0)
d) Cov(X, Y)

Publicado en

1Eva_IIT2010_T2 valor esperado

1ra Evaluación II Término 2010-2011. Diciembre, 2010. FIEC03236

Tema 2 (25 puntos). La función densidad conjunta de dos variables aleatorias está dada por:

f_{XY}(x,y) = k e^{-x} e^{-2y} 0 \leq y \leq x \leq \infty

determinar:
a) P[y ≥ x/2]
b) E[Y|x=3]

Publicado en

3Eva_IIT2009_T3 Densidad espectral de potencia

3ra Evaluación II Término 2009-2010. Febrero 18, 2010. FIEC03236

Tema 3 (30 puntos). Dada la siguiente función de Autocorrelación Rx(ζ) del proceso estocástico X(t) que es WSS.

a) (15 puntos) Encuentre Var[X(t)]
b) (15 puntos) Sx(w) ( o Sx(f))

Transformadas de Fourier

x(t) \rightarrow X(\omega) g(t) \rightarrow \int_{-\infty}^{\infty} g(t) e^{-j2 \pi ft} dt rect\left( \frac{t}{\tau}\right) \rightarrow \tau sinc\left( \frac{\omega \tau}{2}\right) tri\left( \frac{t}{\tau}\right) \rightarrow \frac{\tau}{2} sinc^2(\frac{\omega \tau}{4})
Publicado en

3Eva_IIT2009_T2 autocorrelación

3ra Evaluación II Término 2009-2010. Febrero 18, 2010. FIEC03236

Tema 2 (35 puntos). Sean A y Θ variables aleatorias independientes, A con distribución exponencial de media 1, y Θ con distribución uniforme en el intervalo (0, π/2), es decir las funciones de densidad de A y B son respectivamente:

f_A(a) = e^{-a} , a \in [0,\infty) T_{\Theta}(\theta) = \frac{2}{\pi} , \theta \in [0,\pi /2 ]

Sea X(t) un proceso estocástico definido por:

X(t) = e^{-At}cos(\pi t + 4 \Theta) ; t>0

Calcular:
a) La media y la autocorrelación del proceso X(t).¿Es el proceso estacionario en sentido amplio?
b) La varianza de X(t) y la covarianza entre X(1) y X(2).
c) La función de densidad de probabilidad para X(0)

cos(a ± b) = cos(a)cos(b) ∓ sen(a) sen(b)

Rúbrica: literal a (10 puntos, literal b (10 puntos), literal c (15 puntos)