Publicado en

1Eva_IT2017_T3 Call Center Operadora y Dos Técnicos

1ra Evaluación I Término 2017-2018. Junio 27, 2017

Call Center Operadora y Dos Técnicos

Tema 3 (30 puntos). Para obtener soporte técnico de un proveedor de internet se llama al número telefónico del call-center donde se encuentra una recepcionista y dos técnicos. Los clientes llaman a intervalos de tiempo de 10 minutos, distribuidos exponencialmente.

En una llamada, los clientes son atendidos por la recepcionista que toma los datos y redirige la llamada a uno de los técnicos disponibles. Si un cliente llama mientras la recepcionista atiende otra, el cliente recibe tono de ocupado y la pierde.

La recepcionista al pasar una llamada a los técnicos puede suceder que:

  • Si ambos están disponibles, se selecciona uno con igual probabilidad.
  • Si solo hay uno disponible, se le asigna la llamada.
  • Si los dos técnicos están ocupados, se pierde la llamada.

Considere a un cliente como “satisfecho” si su llamada fue procesada por la recepcionista y cualquiera de los técnicos.
Los tiempos de atención siguen distribuciones exponenciales: recepcionista es de 3 minutos y por técnico es de 15 minutos.

a) ¿Cuáles son los estados para un modelo Markov?
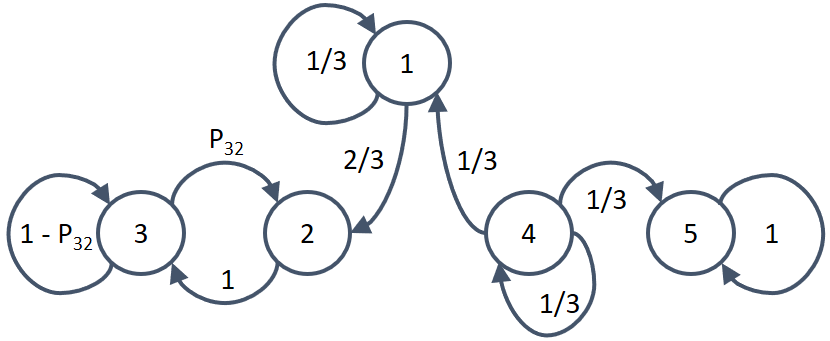
b) Dibuje un modelo de Markov para el problema.
c) Etiquete cada una de las conexiones.
d) En estado estable, ¿cuáles son las probabilidades de encontrarse en cada estado?
e) Encuentre la probabilidad que los técnicos estén ocupados.
f) ¿Cuál es la probabilidad que una llamada se pierda en la recepción?
g) ¿Cuál es la tasa de clientes satisfechos? (salida del sistema, throughput)


Referencias: Chun Tung Chou. COMP9334 Capacity Planning of Computer Systems and Networks.

Rúbrica: literal a y b (10 puntos), literal c (5 puntos), literal d (5 puntos), literal e (4 puntos), literal f y g (6 puntos).

Publicado en

1Eva_IT2017_T2 Cadena de Markov desde diagrama

1ra Evaluación I Término 2017-2018. Junio 27, 2017

Cadena de Markov desde un diagrama de transición de estados

Tema 2 (20 puntos). Considere la siguiente cadena de Markov con estados finitos:

a) Identifique los estados transientes

b) Identifique las clases de los estados recurrentes

c) Para cada clase recurrente, encuentre la probabilidad de estado estable \pi_i . Desarrolle paso a paso.

d) Encuentre las probabilidades de transición para n pasos P_{ij}^{n} como una función de n. Con sus palabras describa cada una (no requiere ecuaciones).

1. P_{44}^n

2. P_{45}^n

3. P_{41}^n

4. P_{43}^n + P_{42}^n

5. \lim_{n \rightarrow \infty} P_{43}^n


Referencia: Chun Tung Chou. COMP9334 Capacity Planning of Computer Systems and Networks. Quiz 2011
Rúbrica: literal a y b (5 puntos), literal c (5 puntos), literal d (10 puntos

Publicado en

1Eva_IT2017_T1 Cadena de Markov desde matriz

1ra Evaluación I Término 2017-2018. Junio 27, 2017

Tema 1 (20 puntos). Dibuje el diagrama de transición de estados y encuentre la distribución (estacionaria) de la cadena de Markov cuya matriz de transición es:

\begin{pmatrix} 1/2 & 1/2 & 0 & 0 \\ 9/10 & 0 & 1/10 & 0 \\ 0 & 1/10& 0 & 9/10\\ 0 & 0 & 1/2 & 1/2 \end{pmatrix}

Nota: Realice el desarrollo paso a paso, planteando las ecuaciones.

Referencia: Prob.12.8. Gubner, J. A. (2006). Probability and random processes for electrical and computer engineers. Cambridge University Press.

Rúbrica: diagrama (5 puntos), desarrollo paso a paso (10 puntos), resultados (5 puntos)

Publicado en

1Eva_IT2010_T5 Pregunta teórica

Tema 5. Responda las siguientes preguntas:

a) Sean i y j estados de una Cadena de Markov estacionaria. Dé una
interpretación a la expresión

f_{ij} = \sum \limits^{\infty}_{n=1} f^{(n)}_{ij}

b) Sea X(t) un proceso estocástico estrictamente estacionario, con función de autocorrelación RX(τ) = E[X(t1)X(t2)], donde τ = t2 − t1.
Entonces, cuál es función de RY(τ) del proceso:

Y(t) := \frac{1}{\epsilon} (X(t+\epsilon)-X(t)) \text { , }\epsilon \in \Re

Referencia: FCNM/ICM01420

Publicado en

1Eva_IT2010_T4 autocorrelaciones para una serie

Tema 4. Asumiendo estacionariedad y con la ayuda de

r_k = \frac{\sum \limits^n_{i=k+1} (x_i-\bar{x})(x_{i-k}-\bar{x})}{\sum \limits^n_{i=1} (x_i-\bar{x})^2 }

a) Encontrar las autocorrelaciones de orden k = 0, 1, 2, 3, 4, 5 para la siguiente serie X = [2, 3, 5, 1, 5, 2], donde xj es un elemento del vector en la posición j, j = 1, . . . , n y bosquejar la gráfica de la función de autocorrelación (ACF).

b) Si las bandas de confianza del gráfico ACF están dadas por \pm z_{\alpha /2}\frac{1}{\sqrt{n}} , ¿es posible decir que con 95% (1 − α = 0,95) puede rechazarse la hipótesis de que todas las autocorrelaciones son cero?.

Publicado en

1Eva_IT2010_T3 Migración urbana, rural, suburbana

Para efectos de una investigación, en un determinado país, una familia puede clasificarse como habitante de zona urbana, rural o suburbana.

Se ha estimado que durante un año cualquiera, el 15% de todas las familias urbanas se cambian a zona suburbana y el 5% a zona rural.

El 6% de las familias suburbanas pasan a zona urbana y el 4% a zona rural.
El 4% de las familias rurales pasan a zona urbana y el 6% a zona suburbana.

a) Defina los estados de este proceso estocástico y escriba la matriz de transición.
Suponga que al inicio de la investigación, el 35% de la población vivía en áreas urbanas, el 45% en áreas suburbanas y el resto en el área rural.

b) Si inicialmente una familia vive en un área rural, cu´al es la probabilidad de que 3 años después esta familia viva en área urbana?.

c) (Probabilidad de un camino). Cuál es la probabilidad que una familia viva en el área urbana y que además en el siguiente año viva en el área suburbana y además luego de eso al siguiente año viva en el área rural.

d) Cuál es la probabilidad de que 3 años después de iniciada la investigación una familia viva en el área urbana?.

Referencia: FCNM/ICM01420

Publicado en

1Eva_IT2010_T2 Jugador con 2 monedas

Tema 2. (Random Walk) Un jugador comienza con $2 en el bolsillo y participa en un juego donde apuesta $1 dólar. 

Gana con probabilidad p y pierde el juego con probabilidad (1−p) = q.

Su meta es aumentar su capital hasta $4 y tan pronto lo logre se saldrá del juego a no ser que caiga en la ruina, es decir que su capital sea $0.

a) Defina los estados de este proceso estocástico y escriba la matriz de transición.

b) Dibuje el diagrama de transición de estados.

c) Escriba las clases de equivalencia (relación de equivalencia $) y los
estados absorbentes, transitorios y recurrentes del proceso cuando
0 < p < 1.

d) Escriba las clases de equivalencia cuando p = 0 e indique cuáles de
estas clases son cerradas y cuáles estados son absorbentes.

Referencia: FCNM/ICM01420

Publicado en

1Eva_IT2010_T1 Urnas de Ehrenfest

Tema 1. (Urnas de Ehrenfest) Se tienen dos urnas, con 5 bolas repartidas dentro de ellas, y en cada etapa se escoge una bola al azar y se cambia de urna.

La cadena Xn representa el número de bolas de una de las urnas tras n etapas.

Escriba la matriz de transición de un paso de esta cadena de Markov.

Referencia: FCNM/ICM01420

Publicado en

1Eva_IIT2009_T5 Manejo de inventarios

Tema 5. Considérese la cadena de Markov Xt que representa el número de unidades que se tienen al final del período t y considérese la política (2,2), es decir si el nivel del inventario al final del período es menor a 2 se ordenan 2 unidades, de otra manera no se ordena.  La demanda tiene distribución Poisson con λ=1.

Suponga que el costo de ordenar es 10 +25 z dólares, si no se ordena el costo es 0 y por cada unidad de demanda insatisfecha se tiene un costo de 50 dólares por unidad.

Encontrar las probabilidades de estado estable y el costo promedio esperado a la larga por unidad de tiempo.

Referencia: FCNM/ICM01420

Publicado en

1Eva_IIT2009_T4 Nacimientos en país poco poblado

Tema 4. Los niños nacen en un país poco poblado, con una frecuencia de un nacimiento cada 12 minutos. El tiempo entre nacimientos sigue una distribución exponencial.

Determinar:

a) La cantidad promedio de nacimientos por año.

b) La probabilidad de que no haya nacimientos en cualquier día.

c) La probabilidad de emitir 50 certificados de nacimientos en 3 horas, cuando se emitieron 40 certificados durante las primeras 2 horas del período de 3 horas

Referencia: FCNM/ICM01420