Publicado en

1. Valor Esperado de una función de variable aleatoria

Referencia: Gubner 2.4 p83 , Ross 2.4.3 p42, León-García 3.3.1 p.107

Dada una variable aleatoria X, se puede definir una nueva variable aleatoria Z = g(X), donde g(x) es una función de valor real de la variable real x.

Para calcular E[Z] se puede proceder como:

E[g(X)] = \sum_i g(x_i) p_X(x_i) E[g(x)] = \int_{-\infty}^{\infty} g(x) f(x) dx

dado que la fórmula es mas fácil de usar que encontrar la pmf de Z, la formula se la conoce como la «ley del estadístico inconsciente» o LOTUS (Law Of The Unconscious Statistician).

Una aplicación simple es :

E[aX] = \sum_i ax_i p_X(x_i) = = a \sum_i x_i p_X(x_i) = a E[X]

Ejemplo

Referencia: León- García 3.17 p107

Sea X el ruido en el voltaje que está uniformemente distribuido en SX = {-3,-1,+1,+3} con pX (k) =  1/4 para k en SX. Encuentre E[Z] donde Z=X2.

Solución: Se busca primero encontrar la pmf (probability mass function) de Z, el SZ ={9,1,1,9} = {1,9}, por lo que:

pZ(9) = P[X ∈ {-3,+3}] 
      = pX(-3) + pX(3) 
      = 1/4 + 1/4 = 1/2
pZ(1) = pX(-1) + pX(1) = 
      = 1/4 + 1/4 = 1/2
entonces:
E[Z] = 1(1/2) + 9(1/2) = 5

usando la fórmula para E[Z]:

E[Z] = E[g(X)] = \sum_i g(x_i)p_X(x_i) = \sum_i i^2 p_X(x_i) = \frac{1}{4} [(-3)^2 + (-1)^2+1^2+2^2] = = \frac{20}{4} = 5

con lo que se obtuvo el mismo resultado.

Ross Corolario 2.2. Siendo a y b constantes, entonces:

E[aX + b] = aE[X] +b
Publicado en

Varianza v.a. Continuas

Referencia: Ross 2.4.3 p43, Gubner 2.4 p84,p150, León-García 4.3.2 p 160

Varianza de variables aleatorias contínuas

el n-ésimo momento, n≥1 de una varial aleatoria X se define como E[Xn].

en el caso continuo.

E[X^n] = \int_{-\infty}^{\infty} x^n f(x) \delta x

El primer momento es la media, E[X].

La varianza σ2 de X se define como:

\text{VAR}[X] = E[(X-E[X])^2]

La varianza de X mide el promedio al cuadrado de la desviación de X del valor esperado.

Algunas propiedade de la varianza, siendo c una constante:

\text{VAR}[c]=0 \text{VAR}[X + c] = \text{VAR}[X] \text{VAR}[cX] = c^2 \text{VAR}[X]

Ejemplo

Encuentre la media y varianza de una variable aleatoria con función de densidad de probabilidad pdf tipo exponencial eλ:

Solucion: dado que VAR[X]= E[x2] – (E[X])2, se calculan los dos momentos de X:

E[X^n] = \int_{0}^{\infty} x^{n} \lambda e^{-\lambda x} \delta x

con cambio de variable y=λx, dy = λdx se tiene que:

E[X^n] = \int_{0}^{\infty} \big( \frac{y}{\lambda} \big) ^{n} e^{-y} \delta y = \frac{1}{\lambda ^n }\int_{0}^{\infty} y^{n} e^{-y} \delta y

si u=yn y dv=e-y dx, entonces du=nyn-1 dx, v = -e-y,
para n=1 el resultado es 1, para n=2 el resultado es 2×1, y para n=3 el resultado es 3x2x1, por lo que el resultado general es n!

E[X^n] = \frac{n!}{\lambda ^n }

la varianza será:

\text{VAR}[X] = E[X^2] - (E[X])^2 = \frac{2}{\lambda ^2} - \big(\frac{1}{\lambda}\big)^2 = \frac{1}{\lambda ^2}
Publicado en

Varianza v.a. discretas

Referencia: Ross 2.4.3 p41, Gubner 2.4 p84, León-García 4.3.2 p 160

Varianza de variables aleatorias discretas

el n-ésimo momento, n≥1 de una variable aleatoria X se define como E[Xn].

en el caso discreto:

E[X^n] = \sum_{x:p(x)>0} x^n p(x)

en el caso continuo.

E[X^n] = \int_{-\infty}^{\infty} x^n f(x) \delta x

El primer momento es la media, E[X].

La varianza σ2 de X se define como:

var(X) = E[(X-E[X])^2]

La varianza de X mide el promedio al cuadrado de la desviación de X del valor esperado.

Ejemplo Gubner 2.27.

Sea X y Y variables aleatorias con sus respectivas funciones de probabilidad de masa, pmf, mostradas en la figura. Calcule var(X) y var(Y)

solución: por simetría, ambas variables tienen media cero, la varianza será:

var(X)= E[(x-E[x])^2] = E[(x-0)^2] = E[x^2] E[X^2] = (-2)^2 \frac{1}{6} + (-1)^2 \frac{1}{3} +(1)^2 \frac{1}{3} +(2)^2 \frac{1}{6} =2 var(Y)= E[(Y-E[Y])^2] = E[(Y-0)^2] = E[Y^2] E[Y^2] = (-2)^2 \frac{1}{3} + (-1)^2 \frac{1}{6} +(1)^2 \frac{1}{6} +(2)^2 \frac{1}{3} =3

X y Y tienen media cero, pero Y tomará valores mas lejanos de su media, dado que var(Y)>var(X).

cuando una variable aleatoria tiene media diferente de cero, puede ser conveniente usar también la fórmula:

var(X) = E[X^2]-(E[x])^2

que indica que la varianza es igual al segundo momento menos el cuadrado del primer momento. Como tarea encuentre la fórmula al reemplazar m=E[X] y desarrollando el cuadrado.

La desviación estándar de X se define como el valor positivo de la raiz cuadrada de la varianza, y se usa el símbolo σ

Ejemplo Ross 2.29

Un sistema de comunicación óptico usa un fotodetector cuya salida es modelada como una variable aleatorioa X tipo Poisson(λ). Encuentre la varianza de X

Solución:

P(X)= \frac{\lambda ^x e^{-\lambda}}{x!} E[x] = \sum_{n=0}^{\infty} n P(X=n) = \sum_{n=0}^{\infty} n \frac{\lambda ^n e^{-\lambda}}{n!}

dado que el término n=0 se puede descartar:

= \sum_{n=1}^{\infty} n \frac{\lambda ^n e^{-\lambda}}{n!} = \sum_{n=1}^{\infty} n\frac{\lambda ^n e^{-\lambda}}{n(n-1)!} = \lambda e^{-\lambda} \sum_{n=1}^{\infty} \frac{\lambda ^{n-1} }{(n-1)!}

cambiando el indice de la suma de n a k=n-1, se tiene que:

\sum_{k=0}^{\infty} \frac{\lambda ^{k} }{k!} = e^{\lambda} E[X]=\lambda e^{-\lambda} \sum_{k=0}^{\infty} \frac{\lambda ^{k} }{k!} = \lambda e^{-\lambda} e^{\lambda} = \lambda

Observe que: E[x2] = E[X(X-1)]+E[X].

Dado que E[X]=λ se calcula que:

E[X(X-1)] = \sum_{n=0}^{\infty} n(n-1) P(X=n) = \sum_{n=2}^{\infty} \frac{\lambda ^n e^{-\lambda}}{(n-2)!} = \lambda ^2 e^{-\lambda} \sum_{n=2}^{\infty} \frac{\lambda ^{n-2}}{(n-2)!}

se tiene nuevamente que, k=n-2:

E[X(X-1)] = \lambda ^2 e^{-\lambda} \sum_{k=0}^{\infty} \frac{\lambda ^{k}}{k!} = \lambda ^2

con lo que E[X2] = λ2 + λ

var(X) = E[X^2] - (E[x])^2 = (\lambda ^2 + \lambda) - \lambda ^2 = \lambda

La variable aleatoria Poisson tiene los valores de media y varianza iguales.

Publicado en

3. Valor Esperado de variables aleatorias contínuas

Referencia: Ross 2.4.2 p39, Gubner 4.2 p149, León-García 4.3 p 155, p16

Si X es una variablea aleatoria contínua que tiene una función densidad de probabilidad f(x), el valor esperado de X se define como:

E[X]= \int_{-\infty}^{\infty}xf(x) \delta x

Ejemplo

Referencia: Ross 4.7.

Sea X una variable aleatoria contínua uniforme [a,b], encuentre el valor esperado:

Solución:

E[X]= \int_{-\infty}^{\infty} xf(x) \delta x = \int_{a}^{b} x\frac{1}{b-a}\delta x = \left. = \frac{1}{(b-a)} \frac{x^2}{2} \right|_{a}^{b} = \frac{1}{(b-a)} \frac{b^2-a^2}{2} = = \frac{(b+a)(b-a)}{2(b-a)} = \frac{a+b}{2}

que es el promedio simple entre a y b cuando la función es uniforme.

Ejemplo

Ross 4.8/Leon-García 4.20. Un convertidor analógico-digital o cuantizador con resolución de paso Δ voltios redondea en la entrada el valor más cercano al múltiplo de Δ voltios como se muestra en la figura.

La entrada es un voltaje Vin de tipo aleatorio y la salida del convertidor es A/D es Vout, y su desempeño se mide por el error cuadratico medio:

E[|Vin – Vout|2]

Se supone que el error Vin – Vout se puede aproximar a una función aleatoria uniforme [-Δ/2,Δ/2] dado que siempre el valor siempre cae en el intervalo dado. Determine el valor esperado para la señal de entrada, y también el valor del error cuadrático medio.

Solución: Para el intervalo centrado en el origen

f(x)= \frac{1}{b-a} E[X] = \int_{-\Delta /2}^{\Delta /2} xf(x) \delta x = =\int_{-\Delta /2}^{\Delta /2} x\frac{1}{\Delta /2 - (-\Delta /2)} \delta x = \int_{-\Delta /2}^{\Delta /2} \frac{x}{\Delta} \delta x = \left. \frac{x^2}{2 \Delta} \right|_{-\Delta /2}^{\Delta /2} = \frac{1}{2\Delta} \big[ {\big( \frac{-\Delta}{2}\big)}^2 - {\big( \frac{\Delta}{2}\big)}^2 \big] = 0

Para el error cuadrático medio en [a,b], a=-Δ/2, b=Δ/2

E[|V_{in}-V_{out}|^2] \approx E[X^2] = \int_{-\infty}^{\infty} x^2 f(x) \delta x = \int_{a}^{b} x^2 \frac{1}{b - a} \delta x = \left. \frac{1}{b-a} \frac{x^3}{3} \right|_{a}^{b} = \frac{1}{b-a} \frac{b^3-a^3}{3} = = \frac{(b-a)(b^2+ba+a^2)}{3(b-a)} = \frac{b^2+ba+a^2}{3} = \frac{({\frac{\Delta}{2})}^2 + {(\frac{\Delta}{2})}{(\frac{-\Delta}{2})} + {(\frac{-\Delta}{2})}^2}{3} = \frac{1}{3} \frac{\Delta ^2 -\Delta^2 + \Delta ^2}{4} = \frac{\Delta ^2}{12}
Publicado en

Variables Aleatorias Contínuas

Referencia: Ross 2.4 p32, Gubner 4.1 p139, León-García 4.1.1 p 146

Una variable aleatoria X se define como una función no negativa f(x) para todos los reales x ∈ (-∞,∞) que tiene la propiedad que para cualquier rango B:
P(X \in B) = \int_B f(x) \delta x

f(x) se conoce como la función densidad de probabilidades o pdf de la variable X, que además satisface:

1 = P(X \in (-\infty,\infty) = \int_{\infty}^{\infty}f(x) \delta x

Si B = [a,b] muestra la función en un intervalo,

p(a \leq X \leq b) = \int_{a}^{b} f(x) \delta x

cuando a=b, se tienen que el integral es cero, lo que muestra que la probabilidad de una variable contínua pueda tomar un valor particular es cero.

Con variables aleatorias contínuas para mejor interpretación se utiliza el valor de la función de distribución acumulada o cdf que se expresa como:

F(a) = P(X \in (-\infty,a]) = \int_{-\infty}^{a} f(x) \delta x

al derivar ambos lados se tiene que:

\frac{\delta}{\delta a} F(a) = f(a)
muestra que la densidad es la derivada de la acumulada.

f_x(x) = \frac{\delta F_x (x)}{\delta x}
Publicado en

PMF – Teclado Qwerty

Referencia: Teclado Qwerty Wikipedia

Uso del teclado QWERTY

El nombre del teclado QWERTY proviene de las primeras seis letras de su fila superior, fue diseñado y patentado por Christopher Sholes en 1868 y vendido a Remington en 1873.

La distribución QWERTY se diseñó con objetivo de separar las letras más usadas de la zona central del teclado, para evitar que se atascaran las máquinas de escribir de primera generación. Actualmente, ésta propiedad no es más requerida, sin embargo se ha heredado la distribución en los teclados de computadora.

A partir de la frecuencia de uso de las letras del alfabeto, se requiere conocer la frecuencia de uso de cada fila del teclado. Los valores de frecuencia para cada letra se encuentran en el archivo: usoletras.txt que por cada línea registra la letra y frecuencia relativa separadas por una coma ‘,’.

archivo: usoletras.txt:
a, 0.11422682511 
b, 0.0118959769969 
c, 0.0464006717728 
d, 0.0543525280541 
...

Algoritmo en Python

# Analiza teclado QWERTY
# Datos desde Archivo 'usoletras.txt'
import numpy as np

# Ingreso
narchivo = input('Nombre del archivo:')
veces    = []
archivo  = open(narchivo,'r')
linea    = archivo.readline()
while not(linea == ''):
    partes = linea.split(',')
    letra  = partes[0]
    frecuencia = float(partes[1])
    veces.append([letra,frecuencia])
    linea = archivo.readline()
archivo.close()

# PROCEDIMIENTO
superior = 'qwertyuiop'
media    = 'asdfghjklñ'
inferior = 'zxcvbnm'
k = len(veces)
usofila = np.zeros(3,dtype=float)
for i in range(0,len(veces),1):
    if (veces[i][0] in superior):
        usofila[0] = usofila[0]+veces[i][1]
    if (veces[i][0] in media):
        usofila[1] = usofila[1]+veces[i][1]
    if (veces[i][0] in inferior):
        usofila[2] = usofila[2]+veces[i][1]

# SALIDA
print(usofila)

resultado:

[ 0.48999975  0.32815084  0.18184941]

La gráfica para pmf se obtiene al añadir las instrucciones:

# GRAFICA
% matplotlib inline
import matplotlib.pyplot as plt
plt.stem([0,1,2],usofila)
plt.title('PMF filas teclado QWERTY')
plt.xlabel('fila superior, media e inferior')
plt.show()

Tarea: En cada caso, realice la gráfica de funciones de probabilidad de masa (pmf) y la función de probabilidades acumulada (cdf)

  • Encuentre la frecuencia de uso de cada mano, presente la división propuesta de el teclado en dos partes: izquierda y derecha.
  • Realice el ejercicio para determinar la frecuencia de uso de cada dedo de cada mano. Presente un modelo gráfico de cada tecla, para mostrar de mejor forma la medida a obtener
  • con los resultados de éste ejercicio, considere llenar la siguiente tabla:
    mano izquierda mano derecha total fila
    superior
    media
    inferior
    total mano
Publicado en

PMF – Alfabeto

Referencia: Ross 2.2 p25, Telex, TTY o teletipo(Wikipedia)

Funciones de probabilidad de masa para alfabeto

Para el «TELEX», «TTY», «teletype» o sistema de tranmisión/recepción de mensajes de texto mecanografiados, al desconocer el contenido del mensaje se podría considerar que cada letra presenta un comportamiento aleatorio. Se puede intuir que hay letras que son poco comunes como ‘x’ y otras muy comunes como ‘e’.

Para el modelo se requiere estimar función de probabilidad de masa (pmf), tomando como base solo el alfabeto incluyendo la letra ‘ñ’, sin discriminar mayúsculas y minúsculas.

Para un ensayo, se usaría un texto con una cantidad considerable de letras, como por ejemplo una obra literaria.

Por ejemplo: ‘elaguacate_Letra.txt‘

Referencia: https://achiras.net.ec/el-aguacate-un-pasillo-ecuatoriano-sin-tiempo/

Para procesar el texto se usa como entrada un archivo en formato .txt, analizando por línea, por símbolo y contando las veces que aparece cada letra del alfabeto. La frecuencia relativa de cada letra respecto al total de letras, permitirá visualizar la forma de la función probabilidad de masa (pmf) para el alfabeto.

Nota: Considere solo el total de letras, no el total de símbolos (no incluye «,;.!?» etc.)

Algoritmo en Python

# procesar un archivo de texto
# Determinar la función de probabilidad de masa
# para las letras del alfabeto(incluye ñ)
import numpy as np

# INGRESO
# archivo=input('archivo a leer.txt: ')
nombrearchivo='elaguacate_Letra.txt'

# PROCEDIMIENTO
alfabeto='abcdefghijklmnñopqrstuvwxyz'
k=len(alfabeto)
veces=np.zeros(k,dtype=int)
total=0
# procesa el archivo
archivo = open(nombrearchivo,'r')
unalinea = archivo.readline()
while not(unalinea==''):
    n=len(unalinea)
    unalinea = unalinea.strip('\n')
    unalinea = unalinea.lower()
    m=len(unalinea)
    for j in range(0,m,1):
        unsimbolo=unalinea[j]
        donde = alfabeto.find(unsimbolo)
        if (donde>=0): #Si no encuentra es negativo
            veces[donde]=veces[donde]+1
            total=total+1
    unalinea = archivo.readline()
archivo.close()

frelativa=veces/total
alfa=np.arange(0,len(alfabeto))

# SALIDA
print('Letras contadas: ', total)
print('i,letra,veces,frelativa')
for i in range(0,len(alfabeto),1):
    print(i, alfabeto[i],veces[i], frelativa[i])

el resultado obtenido es:

Letras contadas:  253
i,letra,veces,frelativa
0 a 25 0.098814229249
1 b 1 0.00395256916996
2 c 5 0.0197628458498
3 d 7 0.0276679841897
4 e 25 0.098814229249
5 f 4 0.0158102766798
6 g 0 0.0
7 h 2 0.00790513833992
8 i 22 0.0869565217391
9 j 1 0.00395256916996
10 k 0 0.0
11 l 15 0.0592885375494
12 m 15 0.0592885375494
13 n 20 0.0790513833992
14 ñ 0 0.0
15 o 24 0.0948616600791
16 p 4 0.0158102766798
17 q 3 0.0118577075099
18 r 16 0.0632411067194
19 s 21 0.0830039525692
20 t 16 0.0632411067194
21 u 16 0.0632411067194
22 v 3 0.0118577075099
23 w 0 0.0
24 x 0 0.0
25 y 7 0.0276679841897
26 z 1 0.00395256916996

para la gráfica se añade al algoritmo:

# GRAFICA
% matplotlib inline
import matplotlib.pyplot as plt
plt.stem(alfa,frelativa)
plt.title('PMF alfabeto')
plt.xlabel(alfabeto)
plt.show()

otro experimento realizado con:
Poe, Edgar Allan. Eureka. Vol. 13. EDAF, 2006.

tiene el siguiente resultado:

Letras contadas:  78598
i,letra,veces,frelativa
0 a 8978 0.11422682511
1 b 935 0.0118959769969
2 c 3647 0.0464006717728
3 d 4272 0.0543525280541
4 e 10455 0.133018651874
5 f 658 0.00837171429298
6 g 818 0.010407389501
7 h 632 0.00804091707168
8 i 5792 0.0736914425303
9 j 161 0.00204839817807
10 k 36 0.000458026921805
11 l 4203 0.0534746431207
12 m 2541 0.0323290668974
13 n 6126 0.0779409145271
14 ñ 46 0.000585256622306
15 o 6725 0.0855619735871
16 p 2271 0.0288938649838
17 q 692 0.00880429527469
18 r 4899 0.0623298302756
19 s 5988 0.0761851446602
20 t 3792 0.0482455024301
21 u 3362 0.0427746253085
22 v 647 0.00823176162243
23 w 34 0.000432580981704
24 x 177 0.00225196569887
25 y 491 0.00624697829461
26 z 220 0.00279905341103

Será necesario que realizar el experimento muchas veces para tener un comportamiento más general, se propone realizar al estudiante su experimento con otros textos.

Con los resultados, se requiere:

  1. Realizar la pmf para vocales
  2. Realizar la pmf para consonantes
  3. determine las letras con menor probabilidad de cada grupo
  4. escriba alguna recomendación para mejorar el experimento
  5. escriba al menos una conlusión

Considere lo siguiente:

Si en una transmisión de texto, por ruido en el canal se cambian aleatoriamente algunos caracteres,

  • ¿Cuáles cambios serían los que afectan menos al mensaje?
  • ¿Cuáles cambios serían los que afectan más al mensaje?

En caso de presentar el resultado de frecuencias relativas en un archivo:

# Archivo
narchivo='usoletras.txt'
archivo=open(narchivo,'w')
for i in range(0,k,1):
    linea=alfabeto[i]+','+str(frelativa[i])+'\n'
    archivo.write(linea)
archivo.close()
Publicado en

Teoría de Colas – Cajeras María y Alicia

Referencia: Ross problema 8.3 p.568

Un administración de un supermercado puede contratar a María o Alicia.

María atiende con una tasa de servicio exponencial de 20 clientes por hora y puede ser contratada por $3/hora.

Alicia atiende con una tasa exponencial de 30 clientes por hora, y puede ser contradada por $C/hora.

El administrador estima que en promedio cada cliente tiene un costo de $1 por hora y debería ser contabilizado para el modelo.

Suponga que los clientes llegan a una tasa Poisson de 10 clientes por hora.

a) ¿Cuál es el costo promedio por hora si María es contratada? o ¿Si Alicia es contratada?

b) Encuentre C si el promedio de costo por hora es el mismo para María y Alicia.

Solución:

a) ¿Cuál es el costo promedio por hora si María es contrada? o ¿Si Alicia es contratada?

λ = 10 clientes/hora

María: 

μMaría = 20 clientes/hora

LMaría = λ/(μ -λ) = 10/(20-10) = 1 

Costo/hora María =  $3 + ($1 * (número promedio de clientes en la cola cuando trabaja María))
      =  $3 + ($1 * LMaría)
      =  $3 + ($1 * 1) = $ 4 

Alicia:
μAlicia = 30 clientes/hora
LAlicia = λ/(μ -λ) = 10/(30-10) = 1/2

Costo/hora Alicia =  $C + ($1 * (número promedio de clientes en la cola cuando trabaja Alicia))
      =  $C + ($1 * LAlicia)
      =  $C + ($1 * 1/2) = $ (C+ 0.5)
      
b) Encuentre C si el promedio de costo por hora es el mismo para María y Alicia.
Costo/hora María = Costo/hora Alicia
 4 = C + 0.5
 C = 3.5 $/hora

 que es lo máximo que el administrador podría pagar a Alice sin incurrir en costos mayores que María, dadas las condiciones del problema.
Publicado en

Teoria de colas – Llegadas Esperadas

Referencia: Ross problema 8.1 p.568

Para una cola M/M/1, calcule

a) el numero esperado de llegadas durante un periodo de servicio
b) la probabilidad que no lleguen clientes durante un periodo de servicio
pista: «condición»

Solución:
a) el numero esperado de llegadas durante un periodo de servicio

E[numero de llegadas] = E[λ S] = λ[1/μ] = λ/μ

b) la probabilidad que no lleguen clientes durante un periodo de servicio

P{0 llegadas} = E[P{0 llegadas | periodo de servicio S}] =
   = E[P{N(S)=0}] = E[e-λS]
E[e^{-\lambda S}] = \int_{0}^{x} e^{-\lambda S}\mu e^{-\mu S}dS = \mu \int_{0}^{\infty} e^{-\lambda S -\mu S}dS = \mu \int_{0}^{\infty} e^{-S(\lambda+\mu)}dS = \left.\frac{-\mu}{\lambda+\mu} e^{-S(\lambda+\mu)}\right|_0^{\infty} = \frac{-\mu}{\lambda+\mu}\left[ e^{-\infty(\lambda+\mu)}-e^{-0(\lambda+\mu)}\right] = \frac{-\mu}{\lambda+\mu} [0-1] = \frac{\mu}{\lambda+\mu}
Publicado en

Teoría de colas – Dos servidores en paralelo

Referencia: Ross 8.17 p.571

Los clientes llegan a una sucursal de dos servidores según a un proceso de Poisson con tasa de dos por hora.

Si al llegar el cliente el servidor 1 esta libre, se atiende con éste.
Si al llegar el cliente el servidor 1 esta ocupado y el servidor 2 esta libre, inicia con el servidor 2.
Clientes que al llegar encuentran los dos servidores ocupados se retiran.

Un cliente que fué atendido por el servidor 1, pasa a ser atendido por el servidor 2 siempre que esté libre, caso contrario sale de la sucursal.
Un cliente al completar el servicio con el servidor 2 sale de la sucursal.
Los tiempos de servicio en los servidores 1 y 2 son variables aleatorias exponenciales con tasas de cuatro y seis por hora.

a) ¿Qué fracción de clientes no entran a la sucursal?

b) ¿Cuál es el valor promedio de tiempo que un cliente que entra, permanece en el sistema?

c) ¿Cuál fracción de los clientes que entraron son atendidos por el servidor 1?

Solución:
Se definen los estados como (servidor1,servidor2), ocupado=0, ocupado=1:

Estado (0,0)
Estado (0,1)
Estado (1,0)
Estado (1,0)

con lo que se contruye el diagrama de estados y transiciones:

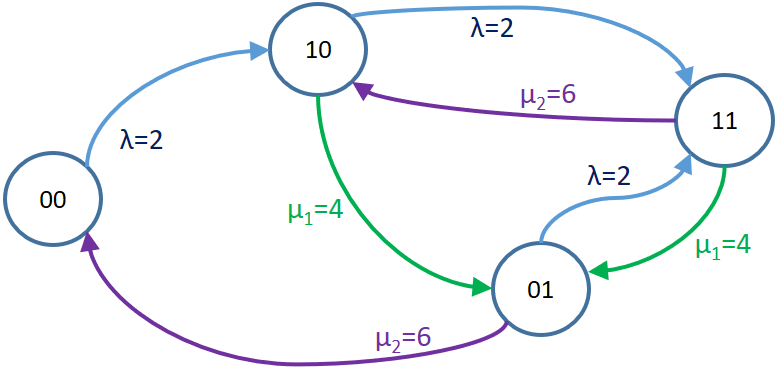
Usando los valores del enunciado se ubican los valores para las tasas de llegada y atención

El siguiente paso consiste en escribir son las ecuaciones de balanceo:

λ P00 = μ2 P01
(μ2 + λ) P01 = μ1 P10 + μ1 P11
(μ1 + λ) P10 = λ P00 + μ2 P11
(μ2 + μ1) P11 = λ P01 + λ P10
1 = P00 + P01 + P10 + P11

usando los valores para λ, μ1 y μ2:

2 P00 = 6 P01
8 P01 = 4 P10 + 4 P11
6 P10 = 2 P00 + 6 P11
10 P11 = 2 P01 + 2 P10
1 = P00 + P01 + P10 + P11

de la ecuación(1)

P01 = (2/6) P00 = (1/3) P00
P01 = (1/3) P00

usando (2) (1/4) y reordenando
2 P01 = P10 + P11
P11 = 2 P01 - P10

sumando con (4)
  P11 = 2 P01 - P10
5 P11 =   P01 + P10

6 P11 = 3 P01
2 P11 = P01
usando (1)
2 P11 = (1/3) P00
  P11 = (1/6) P00

usando (4)
5 P11 =   P01 + P10
5 (1/6) P00 = (1/3) P00 + P10
  P10 = [(5/6) - (1/3)]P00 = [(5-2)/6] P00 = (3/6) P00 = (1/2) P00
  P10 = (1/2) P00 

usando (5) con los resultados dependientes de P00:

1 = P00 + (1/3) P00 +(1/2) P00 + (1/6) P00
1 = [(6+2+3+1)/6] P00 = [12/6] P00 = 2 P00
P00 = 1/2

quedando:
P00 = 1/2
P01 = 1/6
P10 = 1/4
P11 = 1/12

usando numpy de python, se reorganiza las ecuaciones y se crean las matrices:

2 P00 - 6 P01                 = 0
        8 P01 - 4 P10 - 4 P11 = 0
 2 P00        - 6 P10 + 6 P11 = 0
        2 P01 + 2 P10 - 10 P11 = 0
   P00 +  P01 +   P10 +    P11 = 1

import numpy as np
A=np.array([
    [2,-6,0,0],
    [0,8,-4,-4],
    [2,0,-6,6],
    [1,1,1,1]])
B=np.array([0,0,0,1])
P=np.linalg.solve(A,B)
print(P)

[ 0.5         0.16666667  0.25        0.08333333]

que son los resultados anteriores encontrados:

P00 = 0.5
P01 = 0.16666667
P10 = 0.25
P11 = 0.08333333

a) ¿Qué fracción de clientes no entran a la suscursal?

solo ocurre cuando ambos servidores estan ocupados (1,1)

P11 = 1/12 = 0.08333333

b) ¿Cuál es el valor promedio de tiempo que un cliente que entra, permanece en el sistema?

W = L/λ

  = (valor esperado)/(proporcion de los clientes que si entran)
  
  = [0*P00 + 1*P01 + 1*P10 + 2*P11]/ [λ(1-P11)]
  
  = [0*(1/2) + 1*(1/6) + 1*(1/4) + 2*(1/12)]/ [2(1-(1/12)]
  
  = [(0+3+2+2)/12]/[22/12] = (7/12)/(22/12) =  7/22

c) ¿Cuál fracción de los clientes que entraron son atendidos por el servidor 1?

(atiende el servidor 1 cuando esta libre) / (los que entraron)

[P00 + P01] / [1 - P11] = [1/2 + 1/6]/[1 - 1/12]
  
  = [(3+1)/6] / [11/12] = (4/6)/(11/12) =   8/11