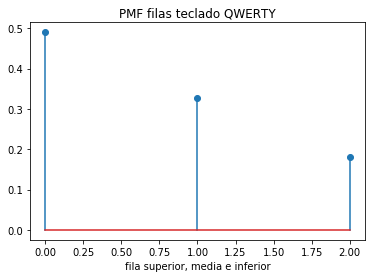
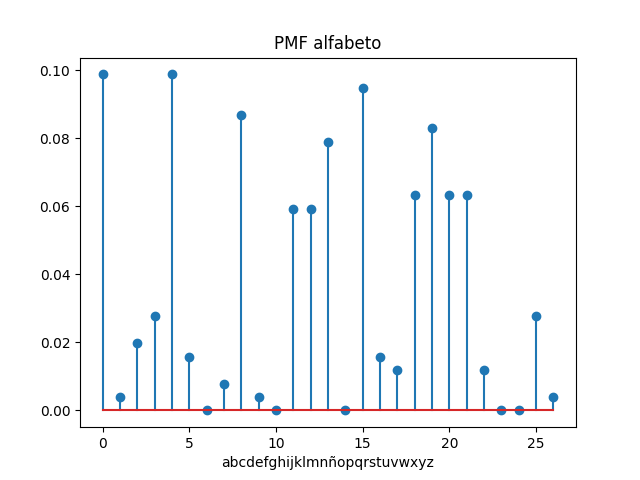
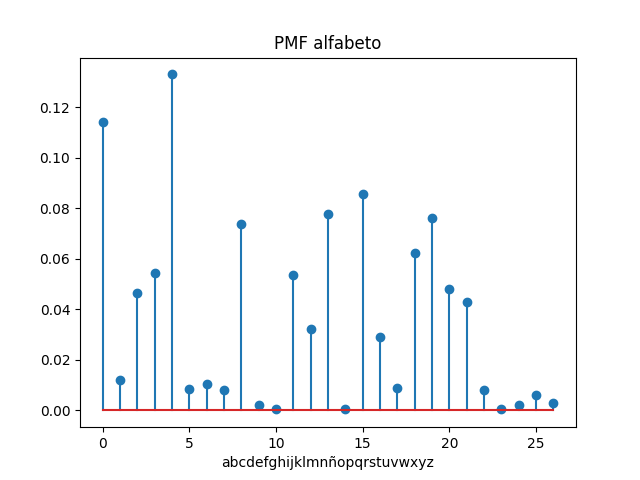
Referencia: Ross 2.4.3 p41, Gubner 2.4 p84, León-García 4.3.2 p 160
Varianza de variables aleatorias discretas
el n-ésimo momento, n≥1 de una variable aleatoria X se define como E[Xn].
en el caso discreto:
E[X^n] = \sum_{x:p(x)>0} x^n p(x)en el caso continuo.
E[X^n] = \int_{-\infty}^{\infty} x^n f(x) \delta xEl primer momento es la media, E[X].
La varianza σ2 de X se define como:
var(X) = E[(X-E[X])^2]La varianza de X mide el promedio al cuadrado de la desviación de X del valor esperado.
Ejemplo Gubner 2.27.
Sea X y Y variables aleatorias con sus respectivas funciones de probabilidad de masa, pmf, mostradas en la figura. Calcule var(X) y var(Y)
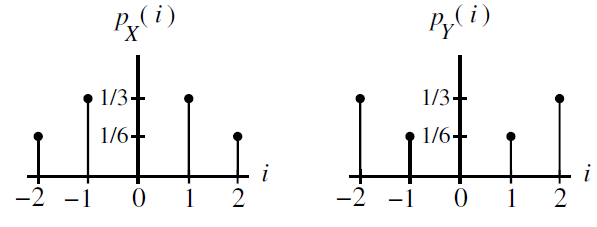
solución: por simetría, ambas variables tienen media cero, la varianza será:
var(X)= E[(x-E[x])^2] = E[(x-0)^2] = E[x^2] E[X^2] = (-2)^2 \frac{1}{6} + (-1)^2 \frac{1}{3} +(1)^2 \frac{1}{3} +(2)^2 \frac{1}{6} =2 var(Y)= E[(Y-E[Y])^2] = E[(Y-0)^2] = E[Y^2] E[Y^2] = (-2)^2 \frac{1}{3} + (-1)^2 \frac{1}{6} +(1)^2 \frac{1}{6} +(2)^2 \frac{1}{3} =3X y Y tienen media cero, pero Y tomará valores mas lejanos de su media, dado que var(Y)>var(X).
cuando una variable aleatoria tiene media diferente de cero, puede ser conveniente usar también la fórmula:
var(X) = E[X^2]-(E[x])^2que indica que la varianza es igual al segundo momento menos el cuadrado del primer momento. Como tarea encuentre la fórmula al reemplazar m=E[X] y desarrollando el cuadrado.
La desviación estándar de X se define como el valor positivo de la raiz cuadrada de la varianza, y se usa el símbolo σ
Ejemplo Ross 2.29
Un sistema de comunicación óptico usa un fotodetector cuya salida es modelada como una variable aleatorioa X tipo Poisson(λ). Encuentre la varianza de X
Solución:
P(X)= \frac{\lambda ^x e^{-\lambda}}{x!} E[x] = \sum_{n=0}^{\infty} n P(X=n) = \sum_{n=0}^{\infty} n \frac{\lambda ^n e^{-\lambda}}{n!}dado que el término n=0 se puede descartar:
= \sum_{n=1}^{\infty} n \frac{\lambda ^n e^{-\lambda}}{n!} = \sum_{n=1}^{\infty} n\frac{\lambda ^n e^{-\lambda}}{n(n-1)!} = \lambda e^{-\lambda} \sum_{n=1}^{\infty} \frac{\lambda ^{n-1} }{(n-1)!}cambiando el indice de la suma de n a k=n-1, se tiene que:
\sum_{k=0}^{\infty} \frac{\lambda ^{k} }{k!} = e^{\lambda} E[X]=\lambda e^{-\lambda} \sum_{k=0}^{\infty} \frac{\lambda ^{k} }{k!} = \lambda e^{-\lambda} e^{\lambda} = \lambdaObserve que: E[x2] = E[X(X-1)]+E[X].
Dado que E[X]=λ se calcula que:
E[X(X-1)] = \sum_{n=0}^{\infty} n(n-1) P(X=n) = \sum_{n=2}^{\infty} \frac{\lambda ^n e^{-\lambda}}{(n-2)!} = \lambda ^2 e^{-\lambda} \sum_{n=2}^{\infty} \frac{\lambda ^{n-2}}{(n-2)!}se tiene nuevamente que, k=n-2:
E[X(X-1)] = \lambda ^2 e^{-\lambda} \sum_{k=0}^{\infty} \frac{\lambda ^{k}}{k!} = \lambda ^2con lo que E[X2] = λ2 + λ
var(X) = E[X^2] - (E[x])^2 = (\lambda ^2 + \lambda) - \lambda ^2 = \lambdaLa variable aleatoria Poisson tiene los valores de media y varianza iguales.