Y(t) = a \cos \big( 2\pi t + \frac{\pi}{2}X(t) \big)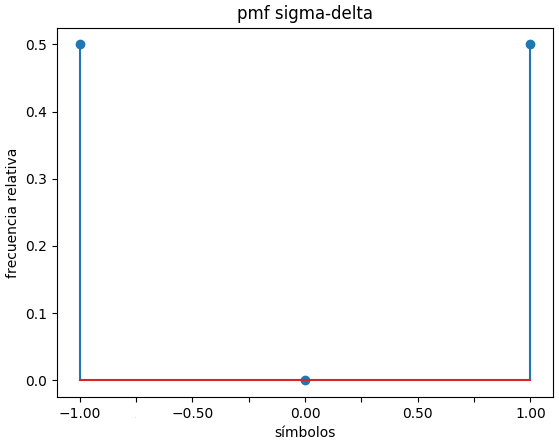
La pmf de x(t) es 0.5 para cada valor de [-1,1]
c) Encuentre la media y autocorrelación de Y(t)
E[Y(t)] = E\big[ a \cos \big( 2\pi t + \frac{\pi}{2}X \big)\big]Referencia: León-García 3.3.1 p. 107. Valor esperado de funciones de variable aleatoria
Si z =g(x)
E[g(x)] = \sum_k g(x_k)p_x(X_k)se tiene entonces que:
= \big[a \cos \big( 2\pi t + \frac{\pi}{2}(-1) \big)\big]\frac{1}{2} + \big[a \cos \big( 2\pi t + \frac{\pi}{2}(1) \big)\big] \frac{1}{2} = \frac{a}{2}\cos \big( 2\pi t - \frac{\pi}{2} \big) + \frac{a}{2}\cos \big( 2\pi t + \frac{\pi}{2} \big) = \frac{a}{2} \sin \big( 2\pi t \big) - \frac{a}{2} \sin \big( 2\pi t \big) = 0 E[Y(t)] = 0