pdf – univariada Ejercicio

Referencia: Ross 2.33 p89

Ejercicio

Sea X una variable aleatoria con densidad de probabilidad:

f(x)= \begin{cases} c(1-x^2)&, -1<x<1 \\ 0 &, \text{en otro caso} \end{cases}

a) ¿Cuál es el valor de c? que permite hacer la función una pdf.

b) ¿Cuál es la función de distribución acumulada de X?

Solución

a)Solo es válido en el rango [-1,1], por lo que el integral es:

1 = \int_{-1}^{1} c(1-x^2) dx = c \int_{-1}^{1} (1-x^2) dx = c \int_{-1}^{1}dx - c \int_{-1}^{1}x^2 dx = c \left. x \right|_{-1}^{1} - c \left. \frac{x^3}{3} \right|_{-1}^{1} = c[1-(-1)] - c\frac{1^3-(-1^3)}{3} = 2c -\frac{2c}{3} 1 = \frac{4c}{3} c=\frac{3}{4}

Solución

b)La función es la integral hasta x:

F(y) = \frac{3}{4} \int_{-1}^{y} (1-x^2) dx = \frac{3}{4} \left. \left[ x - \frac{x^3}{3} \right] \right|_{-1}^{y} = = \frac{3}{4}\left[(y+1) - \left( \frac{y^3}{3} + \frac{1}{3} \right) \right] = F(y) = \frac{3}{4} \left[ y+\frac{2}{3} - \frac{y^3}{3} \right], 1<y<1

---

Instrucciones en Python

usando el resultado anterior:

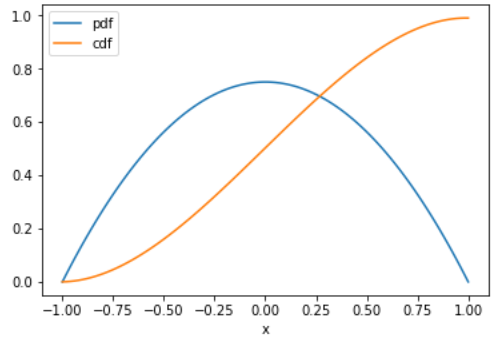
import matplotlib.pyplot as plt
import numpy as np

def fxdensidad(X):
    n = len(X)
    Y = np.zeros(n,dtype=float)
    
    c = 3/4
    for i in range(0,n,1):
        x = X[i]
        if (x>=-1 and x<=1):
            y = c*(1-x**2)
            Y[i] = y
    return(Y)

# INGRESO
# rango [a,b] y muestras
a = -1
b = 1
m = 100

# PROCEDIMIENTO
deltax = (b-a)/m
x  = np.linspace(a,b,m)
fx = fxdensidad(x)

# Función de distribución acumulada
Fy = np.cumsum(fx)*deltax

# SALIDA Gráfico
plt.plot(x,fx,label='pdf')
plt.plot(x,Fy,label='cdf')
plt.xlabel('x')
plt.legend()
plt.show()

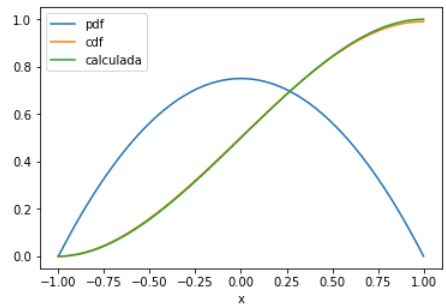
# Verificando resultado del integral vs la suma acumulada
def Fxacumulada(X):
    n = len(X)
    Y = np.zeros(n,dtype=float)
    c = 3/4
    for i in range(0,n,1):
        x=X[i]
        if (x>=-1 and x<=1):
            y=c*(x+ 2/3 -(x**3)/3)
            Y[i]=y
    return(Y)

# PROCEDIMIENTO
Fycalc = Fxacumulada(x)

# SALIDA Gráfico
plt.plot(x,fx,label='pdf')
plt.plot(x,Fy,label='cdf')
plt.plot(x,Fycalc,label='calculada')
plt.xlabel('x')
plt.legend()
plt.show()