Etiqueta: función densidad

3ra Evaluación III Término 2012-2013. Abril 19, 2013. FIEC03236

Tema 3 (10 puntos) Si X es una variable aleatoria uniforme en [-2,2], y se define a Y=|X-1|. Determinar:

a)   F_Y(y)

b)   f_Y(y)

3ra Evaluación III Término 2012-2013. Abril 19, 2013. FIEC03236

Tema 1 (10 puntos). Sea X una variable aleatoria con función de distribución ,

F_X(x) = (1- e^{-\alpha x}) \mu (x-a)

donde α ∈ Re, μ(x) es la función escalón y a ∈ Re⁺.

Determine:

a)   El valor de α.

b)   P(X=a)

Rúbrica: literal a y b (5 puntos)

1ra Evaluación III Término 2012-2013. Marzo 20, 2013. FIEC03236

Tema 2 (30 puntos). La variable aleatoria X tiene por función de densidad f_X(x), y se define la variable aleatoria Y=g(x).

f_X(x) = \begin{cases} k(x+2) && , x \in (-2,0] \\ -k(x-2) && , x \in (0,2] \\ 0 && , x \in (-\infty,-2]\cup(2,\infty) \end{cases}

a) Determinar b para que P(|X|<b) = 1/4

b) Si g(x)=x², encuentre y grafique:

i. La función de distribución de probabilidad de Y
ii. La función de densidad de probabilidad de Y

Rúbrica: literal a 10 puntos, literal b, 10 puntos cada parte.

3ra Evaluación II Término 2012-2013. Febrero 14, 2013. FIEC03236

Una máquina fabrica ejes cuyos radios se distribuyen según una variable aleatoria X cuya función de densidad es:

f_{X}(x) = \begin{cases} k(x-1)(x-3) && , 1 \leq x \leq 3 \\ 0 && \text{otro caso}\end{cases}

La variable aleatoria X se mide en metros.

Determinar:

a) El valor de la constante k.

b) La función de densidad de la variable aleatoria que mide la longitud de los radios en centímetros.

c) La función de densidad para el área de las secciones.

d) Si los ejes se desechan cuando su radio se desvía de 2 metros más de 80cm., calcula la proporción de ejes que serán rechazados.

Rúbrica: literal a (5 puntos), literal b (10 puntos), literal c (10 puntos), literal d (5 puntos)

1ra Evaluación I Término 2011-2012. Julio 7, 2011 . FIEC03236

Tema 3 (20 puntos). Dada la función de distribución de probabilidad F_X(x), encuentre: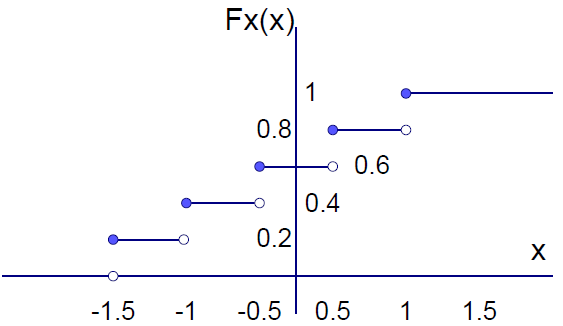
a) P(X = -0.5)
b) P(|X| ≤ 0.5)
c) Dibuje f_X(x|x ≥ -½)
d) Si Y=X+1, dibuje F_Y(y)
e) Determine Var[Y]

Nota: literal a y b (2 puntos), c y d (6 puntos), e (4 puntos)

3ra Evaluación II Término 2010-2011. Febrero 17, 2011. FIEC03236

Tema 1 (25 puntos). Sea X una variable aleatoria con función de densidad de probabilidad uniforme en [-a,a].

Sea Y = g(x) otra variable aleatoria mostrada en la figura: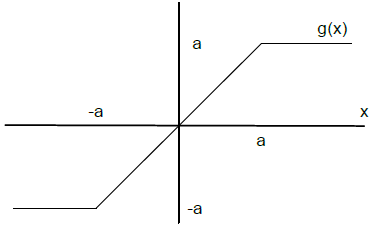

a) Determine y dibuje la función densidad de Y
b) Determine P[ y < a/2]

1ra Evaluación II Término 2010-2011. Diciembre, 2010. FIEC03236

Tema 4 (25 puntos). Sean dos variables aleatorias X, Y independientes entre si con distribución gausiana con parámetros

E[X] = 2
Var[X] = 2
E[Y] = 0
Var[Y] = 1

Se define la variable Z=X+Y.
Determine la función de densidad de probabilidad f_Z(z).