El límite de la función f(x) cuando x se aproxima a p será L si y solo sí para todo ε > 0 existe un δ > 0 tal que para todo número real x en , tenemos que

l siguiente concepto de límite es el de la definición formal, la cual no es muy aprensible para el común de la gente. Dicha formulación matemática es más conocida como epsilon – delta. Por ello es importante entender el concepto de límite como aquella herramienta matemática que sirve para conocer el comportamiento de una función alrededor de un punto, y que no dice nada de tal comportamiento precisamente en dicho punto.

Supóngase f : (M, dM) -> (N, dN) es mapeado entre dos espacios métricos, p es un punto límite de M y L∈N. Decimos que «el límite de f en p es L» y escribimos

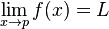
si y sólo si para todo ε > 0 existe un δ > 0 tal que para toda x∈M en 0 < dM(x, p) < δ, tenemos dN(f(x), L) 0 existe un δ (ε) > 0 tal que, para toda x:
si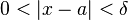entonces
Observemos que la solución de la desigualdad 0 < | x – a | < δ es la siguiente:

x pertenece a la vecindad ( a – δ , a ) U ( a, a + δ ): x no toca el valor de a, pues

0 < | x – a | implica x distinto de a,

mientras que la solución de | f (x) – L | < ε es la siguiente:

y pertenece al intervalo ( L – ε , L + ε ).

Esto proporciona la clave de la comprensión del concepto de límite, pues mientras que el valor de la x está en la vecindad horizontal alrededor del punto «a» y agujereada en «a» con radio delta y centro «a», aun cuando en ese punto «a» no esté definida, el valor de y está en el intervalo vertical con centro en f(a) y radio épsilon.

Funciones de valor real
La recta Real con metricó d(x,y): = | x − y | es un espacio métrico. También la línea Real extendida con métrica d(x,y) = | arctan(x) − arctan(y) | es un espacio métrico.

Límite de una función en un punto
Sea f una función Real, entonces
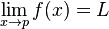(dondey L es un número real)
si y solo si
para todo ε > 0 existe un δ > 0 tal que para todo número real x en 0 < |x-p| < δ, tenemos que |f(x)-L| < ε

Con símbolos: