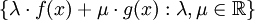Geometría Plana

La historia del origen de la Geometría es muy similar a la de la Aritmética, siendo sus conceptos más antiguos consecuencia de las actividades prácticas. Los primeros hombres llegaron a formas geométricas a partir de la observación de la naturaleza.
El sabio griego Eudemo de Rodas, atribuyó a los egipcios el descubrimiento de la geometría, ya que, según él, necesitaban medir constantemente sus tierras debido a que las inundaciones del Nilo borraban continuamente sus fronteras. Recordemos que, precisamente, la palabra geometría significa medida de tierras.

Los egipcios se centraron principalmente en el cálculo de áreas y volúmenes, encontrando, por ejemplo, para el área del círculo un valor aproximado de ( de 3’1605. Sin embargo el desarrollo geométrico adolece de falta de teoremas y demostraciones formales. También encontramos rudimentos de trigonometría y nociones básicas de semejanza de triángulos. También se tienen nociones geométricas en la civilización mesopotámica, constituyendo los problemas de medida el bloque central en este campo: área del cuadrado, del círculo (con una no muy buena aproximación de (=3), volúmenes de determinados cuerpos, semejanza de figuras, e incluso hay autores que afirman que esta civilización conocía el teorema de Pitágoras aplicado a problemas particulares, aunque no, obviamente, como principio general. No se puede decir que la geometría fuese el punto fuerte de las culturas china e india, limitándose principalmente a la resolución de problemas sobre distancias y semejanzas de cuerpos. También hay quien afirma que estas dos civilizaciones llegaron a enunciados de algunos casos particulares del teorema de Pitágoras, e incluso que desarrollaron algunas ideas sobre la demostración de este teorema…

Actualmente gracias a las muchas culturas y civilizaciones que contribuyeron al avance de la geometria podemos decir que:

La geometría es una rama de las matemáticas que se ocupa de las propiedades del espacio, como son: puntos, rectas, planos, polígonos, poliedros, curvas, superficies, etc. Sus orígenes se remontan a la solución de problemas concretos relativos a medidas y es la justificación teórica de muchos instrumentos, por ejemplo el compás, el teodolito y el pantógrafo.

Así mismo, da fundamento teórico a inventos como el sistema de posicionamiento global (en especial cuando se la considera en combinación con el análisis matemático y sobre todo con las ecuaciones diferenciales) y es útil en la preparación de diseños (justificación teórica de la geometría descriptiva, del dibujo técnico e incluso en la fabricación de artesanías).

La geometría se propone ir más allá de lo alcanzado por la intuición. Por ello, es necesario un método riguroso en el que no se cometan errores; para conseguirlo se han utilizado históricamente los sistemas axiomáticos.

El primer sistema axiomático fue el de Euclides, pero hoy se sabe que este sistema euclídeo es incompleto. David Hilbert propuso a principios del siglo XX otro sistema axiomático, éste ya completo.

Como en todo sistema formal, debe tenerse en cuenta que las definiciones, axiomas y teoremas no sólo pretenden describir el comportamiento de unos objetos. Cuando se axiomatiza algo, se convierte ese comportamiento en el objeto de estudio, pudiendo olvidar ya los objetos iniciales del estudio (que se denominan modelos).

Esto significa que en adelante, las palabras «punto», «recta» y «plano» deben de perder todo significado visual. Si se conserva la idea de punto, recta y plano como lo que comúnmente se comprende como tales, las definiciones y axiomas, e incluso algunos de los teoremas parecerán evidentes y carentes de importancia. Cualquier conjunto de objetos que verifique las definiciones y los axiomas cumplirá también todos los teoremas de la geometría en cuestión, y su comportamiento será virtualmente idéntico al del modelo tradicional.

Por ejemplo, si en la noción de «punto» se considera el modelo en el que un punto cualquiera es un polinomio cualquiera de segundo grado:

si una recta es entonces una familia de polinomios o en lo consiguiente una familia de binomios o monomios de la siguiente manera:

y un plano es entendido como el conjunto:

es posible ver que todos los resultados de las distintas geometrías son válidos para este modelo.

Tipos de Geometría

• Geometría euclidea.
• Geometría analítica.
• Geometría hiperbólica.
• Geometría proyectiva.
• Geometría elíptica.
• Geometría ampudiana
• Geometría analítica
• Geometría diferencial
• Geometría euclídea
• Geometría euclidiana
• Geometría proyectiva
• Geometría descriptiva
• Geometría espacial
• Geometría de incidencia
• Geometría de dimensiones bajas
• Geometría plana

Es este blog nos centraremos en el estudio de la Geometria Plana.

La Geometría plana

Es la rama de la geometría elemental que estudia las propiedades de superficies y figuras planas, como el triángulo o el círculo. Esta parte de la geometría también se conoce como geometría euclídea, en honor al matemático griego Euclides, el primero en estudiarla en el siglo IV a.C. Su extenso tratado Elementos de geometría se mantuvo como texto autorizado de geometría hasta la aparición de las llamadas Geometría no euclideas en el siglo XIX.

De aqui a la geometría la estudiaremos por partes:

Revisar Páginas

• Los triángulos
• Los cuadriláteros
• Los polígonos
• La circunferencia y circulos
• Áreas y perímetros

PUNTO