Ejercicio: 3Eva2016TI_T4 rampa(ω) – transformada inversa de Fourier

la función de magnitud |X(ω)|  es par en el eje vertical,

usando la derivada de |X(ω)|,

la expresión de la gráfica usando impulsos y rectángulos en dominio ω es,

\frac{\delta}{\delta \omega}X(\omega) = \delta( \omega +\omega_0) - \frac{1}{\omega_0} P_{\omega_0/2}\Big( \omega +\frac{\omega_0}{2}\Big)

+ \frac{1}{\omega_0} P_{\omega_0/2}\Big( \omega -\frac{\omega_0}{2}\Big) - \delta( \omega - \omega_0)

aplicando la transformada inversa de Fourier

\mathscr{F} ^{-1} \Big[ \frac{\delta}{\delta \omega}X(\omega) \Big] = \mathscr{F} ^{-1} \Big[\delta( \omega +\omega_0) - \frac{1}{\omega_0} P_{\omega_0/2}\Big( \omega +\frac{\omega_0}{2}\Big) \Big]

+ \mathscr{F} ^{-1} \Big[\frac{1}{\omega_0} P_{\omega_0/2}\Big( \omega -\frac{\omega_0}{2}\Big) - \delta( \omega - \omega_0) \Big]

si se realiza por partes, y considerando solo la gráfica de magnitud |X(ω)|

\mathscr{F} ^{-1} \Big[ \frac{\delta}{\delta \omega}X(\omega) \Big] = -jtx_1(t)

\mathscr{F} ^{-1} \Big[\delta( \omega +\omega_0)\Big] = \frac{1}{2\pi} e^{-j\omega_0 t}

\mathscr{F} ^{-1} \Big[\frac{1}{\omega_0} P_{\omega_0/2}\Big( \omega +\frac{\omega_0}{2}\Big) \Big] = \frac{1}{\omega_0} \frac{1}{\pi t} \sin \Big(\frac{\omega_0}{2} t \Big) e^{-j\frac{\omega_0}{2}t}

sustituyendo en la ecuación principal,

-jtx_1(t) = \frac{1}{2\pi} e^{-j\omega_0 t} - \frac{1}{\omega_0} \frac{1}{\pi t} \sin \Big(\frac{\omega_0}{2} t \Big) e^{-j\frac{\omega_0}{2}t}

+ \frac{1}{\omega_0} \frac{1}{\pi t} \sin \Big(\frac{\omega_0}{2} t \Big) e^{j\frac{\omega_0}{2}t} - \frac{1}{2\pi} e^{j\omega_0 t}

agrupando,

-jtx_1(t) = \frac{1}{2\pi}\Big( e^{-j\omega_0 t} -e^{j\omega_0 t}\Big)

+ \frac{1}{\omega_0 \pi t} \sin \Big(\frac{\omega_0}{2} t \Big)\Big(- e^{-j\frac{\omega_0}{2} t} +e^{j\frac{\omega_0}{2} t}\Big)

para simplificar se divide ambos lados de la ecuación para -jt

x_1(t) = \frac{1}{\pi t}\Big( \frac{e^{j\omega_0 t}-e^{-j\omega_0 t} }{2j}\Big)

- \frac{2}{\omega_0 \pi t^2 } \sin \Big(\frac{\omega_0}{2} t \Big)\Big(\frac{e^{j\frac{\omega_0}{2} t}- e^{-j\frac{\omega_0}{2} t}}{2j}\Big)

que es la forma exponencial del seno y coseno

x_1(t) = \frac{1}{\pi t} \sin (\omega_0 t) - \frac{2}{\omega_0 \pi t^2 } \sin \Big(\frac{\omega_0}{2} t \Big) \sin \Big( \frac{\omega_0}{2} t \Big)

x_1(t) = \frac{1}{\pi t}\sin (\omega_0 t) - \frac{2}{\omega_0 \pi t^2 }\sin^2 \Big(\frac{\omega_0}{2} t \Big)

x_1(t) = \frac{\omega_0}{\pi}\frac{\sin (\omega_0 t)}{\omega_0 t} - \frac{\omega_0}{2\pi}\Bigg[\frac{\sin \Big(\frac{\omega_0}{2} t \Big)}{\frac{\omega_0}{2} t} \Bigg]^2

ahora, considerando la gráfica de fase:

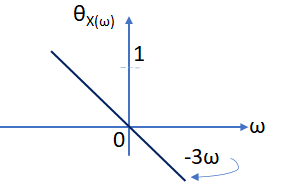
se tiene que,

x(t) = x_1(t-3)

x(t) = \frac{\omega_0}{\pi}\frac{\sin (\omega_0 (t-3))}{\omega_0 (t-3)} - \frac{\omega_0}{2\pi}\Bigg[\frac{\sin \Big(\frac{\omega_0}{2} (t-3) \Big)}{\frac{\omega_0}{2} (t-3)}\Bigg]^2

Ejercicio: 3Eva2016TI_T3 LTI CT Circuito RL respuesta de frecuencia

a. Determinar su función de transferencia

voltaje en la entrada,

v_1(t) = v_R(t) + v_L(t)

v_1(t) = R i(t) + v_L(t)

voltaje en la salida,
v_2(t) = L \frac{\delta}{\delta t}i(t)

i(t) = \frac{1}{L} \int_{-\infty}^{t}v_2(\tau) \delta \tau

sustituyendo i(t)en la ecuacion de v₁

v_1(t) = R \frac{1}{L} \int_{-\infty}^{t}v_2(\tau) \delta \tau + v_L(t)

usando un solo operador, el diferencial,

\frac{\delta}{\delta t} v_1(t) = \frac{R}{L} v_2(t) + \frac{\delta}{\delta t} v_2(t)

cambiando al dominio de frecuencia ω

j\omega V_1(\omega) = \frac{R}{L} V_2(\omega) + j\omega V_2(\omega)

j\omega L V_1(\omega) = R V_2(\omega) + j\omega L V_2(\omega)

j\omega L V_1(\omega) = V_2(\omega)\Big( R + j\omega L \Big)

H(\omega) = \frac{V_2(\omega)}{V_1(\omega)} = \frac{j\omega L}{ R + j\omega L }

H(\omega) = \frac{j\omega \frac{L}{R}}{ 1 + j\omega \frac{L}{R} }

usando los valores del circuito

H(\omega) = \frac{j\omega 0.2}{ 10 + j\omega 0.2 }

H(\omega) = \frac{j\omega}{50 + j\omega }

|H(\omega)| = \frac{|\omega|}{\sqrt{ 50^2 + \omega^2} }

\theta_{H(\omega)} = \frac{\pi}{2} - \arctan \Big( \frac{\omega}{50}\Big)

\omega_0 = \frac{R}{L} = \frac{10}{0.2} = 50 rad/s

b. Determinar, esquematizar y etiquetar su respuesta de frecuencia, indicando a que tipo de filtro no ideal de frecuencias selectivas se podría asociar su comportamiento.

tarea...

c. Obtener la respuesta impulso h(t) que representa al circuito eléctrico.

h(t) = \mathscr{F} ^{-1} \Big[ H(\omega) \Big]

= \mathscr{F} ^{-1} \Big[ \frac{j\omega}{50 + j\omega } \Big]

separando en fracciones parciales y usando la tabla de transformadas de Fourier:

= \mathscr{F} ^{-1} \Big[ 1-\frac{50}{50 + j\omega } \Big]

h(t) = \delta (t) - 50 e^{-50t} \mu (t)

d. Determinar la respuesta v₂(t) que se obtiene a la salida de dicho sistema cuando tiene una entrada v₁(t) = sen 50t [V].
¿Qué puede decir acerca de si el sistema transmite con distorsión o sin distorsión? Justifique su respuesta de manera razonada.

V_1(\omega) = \mathscr{F} \Big[ v_1(t)\Big] = \mathscr{F} \Big[ \sin (50t) \Big]

= j\pi \delta (\omega+50) - j\pi \delta (\omega-50)

V_2(\omega) = V_1(\omega) H(\omega)

V_2(\omega) =\Big( j\pi \delta (\omega+50) - j\pi \delta (\omega-50) \Big) \Big( \frac{j\omega}{50 + j\omega } \Big)

=j^2\pi \Big( \delta (\omega+50) \frac{\omega}{50 + j\omega } - \delta (\omega-50) \frac{\omega}{50 + j\omega }\Big)

= (-1)\pi \Big( \delta (\omega+50) \frac{\omega}{50 + j\omega }- \delta (\omega-50) \frac{\omega}{50 + j\omega }\Big)

Los términos con impulso desplazados tienen magnitud solo en las posiciones donde el impulso tiene valor 1. En este caso es con ω=±50

V_2(\omega) =\pi \Big( \delta (\omega+50) \frac{(-1)(-50)}{50 - j50 } - \delta (\omega-50) \frac{(-1)50}{50 + j50}\Big)

dividiendo el numerador y denominador para 50 se simplifica a

=\pi \Big( \delta (\omega+50) \frac{1}{1 - j1 } + \delta (\omega-50) \frac{1}{1 + j1}\Big)

multiplicando el primer coeficiente por 1+j y el segundo coeficiente por 1-j, se convierte el denominador en un número real.

=\pi \Big( \delta (\omega+50) \frac{1(1+j)}{(1 - j1) (1+j)} + \delta (\omega-50) \frac{1(1-j)}{(1 + j1)(1-j)}\Big)

=\pi \Big( \delta (\omega+50) \frac{1+j}{2} + \delta (\omega-50) \frac{1-j}{2}\Big)

=\frac{\pi}{2} \Big( \delta (\omega+50)+j\delta (\omega+50) + \delta (\omega-50) - j\delta (\omega-50) \Big)

V_2(\omega) =\frac{\pi}{2} \Big( \delta (\omega+50) + \delta (\omega-50)\Big) + j\frac{\pi}{2} \Big(\delta (\omega+50)- \delta (\omega-50) \Big)

obteniendo v₂(t) en el dominio de tiempo,

v_2(t) = \mathscr{F}^{-1} \Big[V_2(\omega) \Big]

=\frac{1}{2} \mathscr{F}^{-1} \Bigg[ \pi \Big(\delta (\omega+50) + \delta (\omega-50) \Big )\Bigg] +

+\frac{1}{2} \mathscr{F}^{-1} \Bigg[ j\pi \Big(\delta (\omega+50) + \delta (\omega-50) \Big )\Bigg]

v_2(t) =\frac{1}{2} \cos(50t) + \frac{1}{2} \sin(50t)

por magnitud y fase, simplificación trigonométrica

v_2(t) =\frac{1}{\sqrt{2}} \sin\Big(50t+\frac{\pi}{4}\Big)

también con Sympy,

>>> v2=(1/2)*sym.cos(50*t)+(1/2)*sym.sin(50*t)
>>> sym.trigsimp(v2)
0.5*sqrt(2)*sin(50*t + pi/4)
>>> 

el resultado es concordante con lo que realiza la función de transferencia, respuesta al impulso H(ω) en ω=50

|H(\omega)| = \frac{|\omega|}{\sqrt{ 50^2 + \omega^2} }

= \frac{|50|}{\sqrt{ 50^2 + 50^2} } = \frac{|50|}{\sqrt{ 2(50^2)} } = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}

\theta_{H(\omega)} = \frac{\pi}{2} - \arctan \Big( \frac{\omega}{50}\Big)

= \frac{\pi}{2} - \arctan \Big( \frac{50}{50}\Big) = \frac{\pi}{2}-\frac{\pi}{4} = \frac{\pi}{4}

considerando también que:

\omega_0 = \frac{R}{L} = \frac{10}{0.2} = 50 rad/s

Ejercicio: 3Eva2016TI_T2 LTI CT sub-sistemas h(t) multiplicados con Fourier

a. Determinar la energía contenida en la señal h(t)

h(t) = \frac{\sin (11 \pi t)}{\pi t}

E_{h(t)} = \int_{-\infty}^{\infty} |h(t)|^2 \delta t = \frac{1}{2\pi} \int_{-\infty}^{\infty}|H(\omega)|^2 \delta \omega

= \frac{1}{2\pi} \int_{-11\pi}^{11\pi}|1|^2 \delta \omega = \frac{1}{2\pi} \omega \Big|_{-11\pi}^{11\pi}

= \frac{1}{2\pi} \big(11\pi-(-11\pi)\big)

= \frac{1}{2\pi} 2\big(11\pi\big) = 11

b. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal m(t). Es decir M(ω) vs ω.

X(\omega) = \mathscr{F} \Big[\sum_{i=1}^{\infty} \frac{1}{k^2} \cos(5k\pi t) \Big]

= \sum_{i=1}^{\infty} \frac{1}{k^2} \mathscr{F} \Big[\cos (5k\pi t) \Big]

= \sum_{i=1}^{\infty} \frac{1}{k^2} \Big[\pi \delta (\omega +5k\pi) + \pi \delta (\omega -5k\pi) \Big]

X(\omega) = \pi \sum_{i=1}^{\infty} \frac{1}{k^2} \Big[\delta (\omega +5k\pi) +\delta (\omega -5k\pi) \Big]

Para el caso de la función de transferencia H(ω) que representa un filtro pasabajo LPF,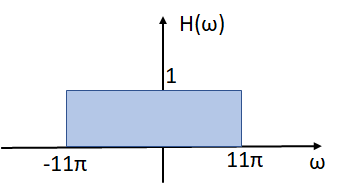

H(\omega) = \mathscr{F} \Big[\frac{\cos (11 \pi t)}{\pi t} \Big] = p_{11\pi}(\omega)

-11\pi \lt \omega \lt 11\pi

M(\omega) = X( \omega ) H( \omega )

= p_{11\pi}(\omega) \sum_{i=1}^{\infty} \frac{1}{k^2} \pi\Big[\delta (\omega +5k\pi) +\delta (\omega -5k\pi) \Big]

por el filtro pasabajo  LPF se limitan las señales hasta k=2

= \sum_{i=1}^{2} \frac{1}{k^2} \pi\Big[\delta (\omega +5k\pi) +\delta (\omega -5k\pi) \Big]

= \pi \frac{1}{1^2} \Big[\delta (\omega +5\pi) +\delta (\omega -5\pi) \Big]

+ \pi \frac{1}{2^2} \Big[\delta (\omega +5(2)\pi) +\delta (\omega -5(2)\pi) \Big]

= \pi \delta (\omega +5\pi) +\pi \delta (\omega -5\pi)

+ \frac{\pi}{4} \delta (\omega +10\pi) +\frac{\pi}{4} \delta (\omega -10\pi)

c. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal n(t). Es decir N(ω) vs ω

N(\omega) = G( \omega ) H( \omega )

N(\omega) = G( \omega ) \mathscr{F} \Big[\sum_{k=1}^{10} \cos (8k \pi t) \Big]

= p_{11\pi}(\omega) \sum_{i=1}^{10} \pi\Big[\delta (\omega +8k\pi) +\delta (\omega -8k\pi) \Big]

por el filtro pasabajo LPF se limitan las señales hasta k=1

= \pi \sum_{i=1}^{1} \Big[\delta (\omega +8k\pi) +\delta (\omega -8k\pi) \Big]

= \pi \Big[\delta (\omega +8\pi) +\delta (\omega -8\pi) \Big]

= \pi \delta (\omega +8\pi) + \pi\delta (\omega -8\pi)

d. Determinar la potencia de la señal de salida y(t) y la representación de su espectro de Series de Fourier complejas exponenciales. Indique también el orden de los armónicos que están presentes en dicha salida.

Z(\omega) = \mathscr{F}[m(t) n(t)] = \frac{1}{2 \pi} M(\omega) \circledast N(\omega)]

= \frac{1}{2 \pi} \Big[\pi \delta (\omega +5\pi) +\pi \delta (\omega -5\pi) +

+\frac{\pi}{4} \delta (\omega +10\pi) +\frac{\pi}{4} \delta (\omega -10\pi)\Big] \circledast \Big[ \pi \delta (\omega +8\pi) + \pi\delta (\omega -8\pi) \Big]

se obtiene factor común π,  para simplificar

Z(\omega) = \frac{\pi^2}{2\pi} \Big[\delta (\omega +5\pi) + \delta (\omega -5\pi) +

+\frac{1}{4} \delta (\omega +10\pi) +\frac{1}{4} \delta (\omega -10\pi)\Big] \circledast \Big[ \delta (\omega +8\pi) + \delta (\omega -8\pi) \Big]

= \frac{\pi}{2} \Big[\delta (\omega +5\pi+8\pi) + \delta (\omega -5\pi+8\pi) +

+\frac{1}{4} \delta (\omega +10\pi +8\pi) +\frac{1}{4} \delta (\omega -10\pi +8\pi)

+\delta (\omega +5\pi-8\pi) + \delta (\omega -5\pi-8\pi) +

+\frac{1}{4} \delta (\omega +10\pi -8\pi) +\frac{1}{4} \delta (\omega -10\pi -8\pi) \Big]

Z(\omega) = \frac{\pi}{2} \Big[\delta (\omega +13\pi) + \delta (\omega +3\pi) +

+\frac{1}{4}\delta (\omega +18\pi) +\frac{1}{4} \delta (\omega -2\pi)

+ \delta (\omega -3\pi) + \delta (\omega -13\pi) +

+\frac{1}{4} \delta (\omega +2\pi) +\frac{1}{4} \delta (\omega -18\pi)\Big]

d. Determinar la potencia de la señal de salida y(t) y la representación de su espectro de Series de Fourier complejas exponenciales. Indique también el orden de los armónicos que están presentes en dicha salida.

Y(\omega) = Z(\omega) H(\omega)] = p_{11\pi}(\omega)Z(\omega)

Las frecuencias superiores a 11ω no pasan por el filtro LPF

Z(\omega) = \frac{\pi}{2} \Big[\cancel{\delta (\omega +13\pi)} + \delta (\omega +3\pi) +

+\cancel{\frac{1}{4}\delta (\omega +18\pi)} +\frac{1}{4} \delta (\omega -2\pi)

+ \delta (\omega -3\pi) + \cancel{\delta (\omega -13\pi)} +

+\frac{1}{4} \delta (\omega +2\pi) +\cancel{\frac{1}{4} \delta (\omega -18\pi)}\Big]

Y(\omega)= \frac{\pi}{2} \Big[\delta (\omega +3\pi) + \delta (\omega -3\pi) +

+\frac{1}{4} \delta (\omega +2\pi) + \frac{1}{4} \delta (\omega -2\pi)\Big]

Y(\omega)= \frac{\pi}{2}\delta (\omega +3\pi) + \frac{\pi}{2}\delta (\omega -3\pi) +

+\frac{\pi}{8} \delta (\omega +2\pi) + \frac{\pi}{8} \delta (\omega -2\pi)

ordenando y agrupando para obtener la inversa de la transformada,

Y(\omega)= \frac{1}{8} \pi \Big[ \delta (\omega +2\pi) + \delta (\omega -2\pi) \Big]

+\frac{1}{2} \pi\Big[\delta (\omega +3\pi) + \delta (\omega -3\pi) \Big]

 

y(t) = \mathscr{F}^{-1}\Big[ Y(\omega) \Big]

y(t) = \frac{1}{8}\cos (2 \pi t) + \frac{1}{2}\cos (3 \pi t)

para determinar las frecuencias fundamentales de y(t) se tiene:

\omega_1 = 2\pi f = \frac{2\pi}{T_1} =2 \pi

T_1 = \frac{2\pi}{2\pi} =1

\omega_2 = 2\pi f = \frac{2\pi}{T_2} =3 \pi

T_2 = \frac{2\pi}{3\pi} = \frac{2}{3}

\frac{T_1}{T_2} = \frac{1}{2/3} =\frac{3}{2}

la relación entre los periodos fundamentales es racional, se tiene que la señal de salida y(t) es periódica.

2T_1 = 3T_2 =T_0

2(1) = 3 \frac{2}{3} = 2 =T_0

\omega_0 = \frac{2\pi}{T_0} =\frac{2\pi}{2} = \pi

los armónicos se pueden obtener observando la gráfica de y(ω):

k₁ = 2, k₂=3

para la potencia de la señal de salida y(t) se puede aplicar la relación de Parseval, siendo C_k los coeficientes de cada cos() para cada ω_k, y C₀ es cero por no tener componente en ω₀=π

P_{y(t)} = C_o^2 + \frac{1}{2} \sum_{k=1}^{\infty} |C_k|^2

=(0)^2 + \frac{1}{2} \Big[ \Big(\frac{1}{8}\Big)^2 + \Big( \frac{1}{2}\Big) ^2 \Big]

=(0)^2 + \frac{1}{2} \Big[ \frac{1}{64} +\frac{1}{4} \Big] = \frac{1}{2}\Big(\frac{1}{4}\Big) \Big[ \frac{1}{16} +1 \Big]

= \frac{1}{8} \frac{17}{16} = \frac{17}{128}