Categoría: Evaluaciones

Ejercicios de examen

Publicado el

1Eva2016TII_T1 LTI CT subsistema en paralelo-serie

1ra Evaluación II Término 2016-2017. 8/Diciembre/2016. TELG1001

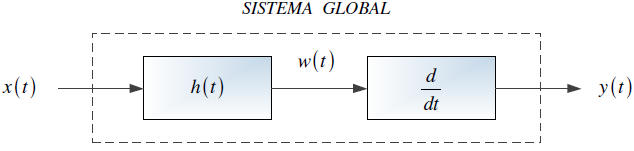
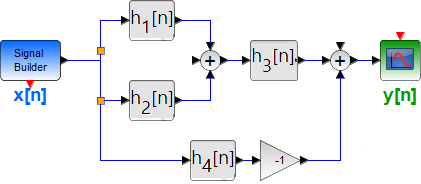
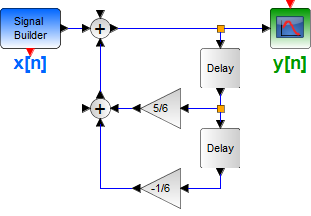
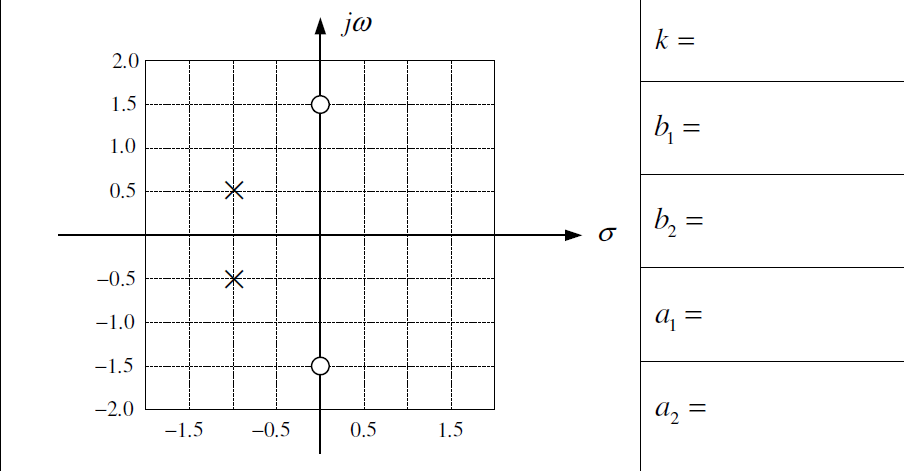
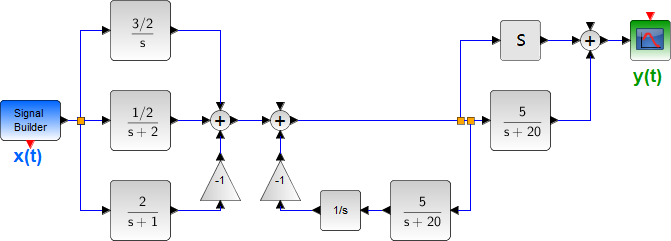
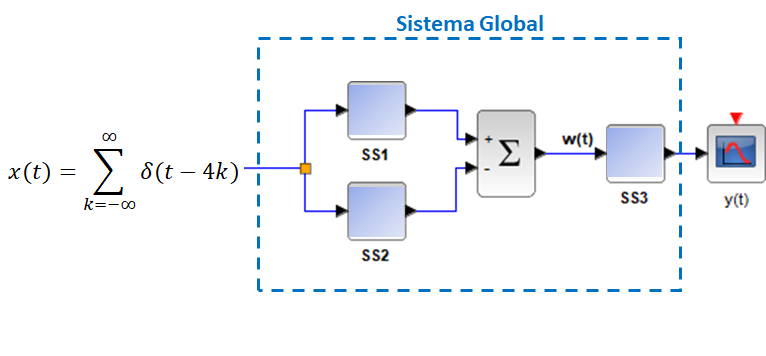
Tema 1. (28 puntos) Considere la existencia de un sistema global LTI-CT que ha sido integrado por la conexión en paralelo de dos subsistemas LTI-CT (SS1 y SS2). El sistema equivalente, es a su vez conectado en serie con otro subsistema LTI-CT (SS3).

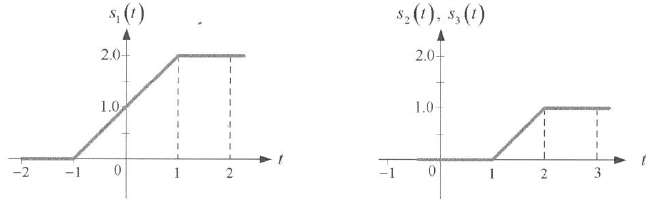
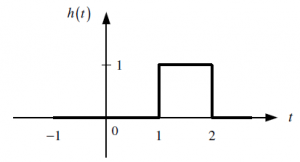
"Respuestas de paso", y(t) ante una entrada escalón unitario x(t) = μ(t) se etiquetan como s(t)

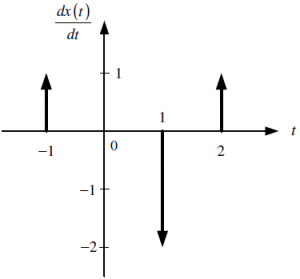
El sistema global es excitado por x(t), conformado porun tren de impulsos unitarios, tal como se muestra en la figura. Conociendo las respuestas de paso de los subsistemas SS1, SS2 y SS3, se requiere lo siguiente:

a. Determinar las respuestas impulso de los subsistemas SS1, SS2 y SS3. es decir h1(t), h2(t), h3(t).

b. Determine la respuesta de paso (x(t) = μ(t)) del subsistema combinado SS12, es decir s12(t).

c. Determinar, esquematizar y etiquetar la respuesta impulso del sistema global, es decir h123(t). Encierre en un círculo la respuesta correcta en la tabla de éste enunciado.

literal b
Sistema SS1 Sistema SS2 Equivalente SS1 y SS2 Sistema SS3 SISTEMA GLOBAL
CON MEMORIA Si No Si No Si No Si No Si No
CAUSAL Si No Si No Si No Si No Si No
BIBO ESTABLE Si No Si No Si No Si No Si No

d. Determinar, esquematizar y etiquetar la respuesta w(t) que se genera a la salida del subsistema SS12, asi como su correspondiente potencia normalizada Pw(t).

d. Determinar, esquematizar y etiquetar la respuesta y(t) del precitado sistema global frente a la excitación x(t), asi como su correspondiente potencia normalizada Py(t).

Se debe presentar la justificación de su respuesta en las hojas de desarrollo. Tome en cuenta todas las consideraciones necesarias para presentar su respuesta.

Coordinador: Tama Alberto

Publicado el

1Eva2011TII_T3 LTI CT H(s) desde expresión con operadores D

1ra Evaluación II Término 2011-2012. 1/Diciembre/2011. TELG1001

Tema 2. (40 puntos) Considere la existencia de un sistema LTI-CT, cuya representación mediante el uso de operadores es la siguiente:

(D^2 + 3 D -28) y(t) = (15D+72) x(t)

Adicionalmente, se conoce que la Región de Convergencia de la función de transferencia del referido sistema es -7 < Re(s) < 4.

Determinar,

a. La función de transferencia H(s) y esquematizar en el plano complejo su diagrama de polos y ceros. Comente sobre la estabilidad del sistema, justificando debidamente su respuesta.

b. La respuesta impulso h(t) de dicho sistema, y la obtención de su valor inicial y final a partir de la aplicación del TVI y TVF.

c. La representación del mencionado sistema, en el dominio de tiempo contínuo, mediante diagrama de bloques.

d. La respuesta de dicho sistema frente a la entrada:

x(t) = e^{-5t} \mu (t)

Referencia: 1Eva2016TII_T2 LTI CT bloques en paralelo-serie con Laplace ,  1Eva2012TII_T4 LTI CT bloques en paralelo-serie con Laplace

Publicado el

1Eva2011TII_T2 LTI CT Respuestas de subsistemas en serie

1ra Evaluación II Término 2011-2012. 1/Diciembre/2011. TELG1001

Tema 2. (30 puntos) Para el sistema LTI_CT integrado por la conexión en serie de dos subsistemas; y conociendo la señal de entrada x(t) junto a la respuesta impulso h(t) para el primer subsistema, se requiere:

a. Determinar, esquematizar y etiquetar la respuesta w(t) que se genera a la salida del primer subsistema, asi como su correspondiente energía.

b. Obtener, esquematizar y etiquetar la salida y(t) que genera el sistema global, así como su correspondiente energía.

c. Conociendo la existencia de la señal z(t), expresar w(t) como una función de  z(t).

Publicado el

1Eva2011TII_T1 LTI DT en serie-paralelo

1ra Evaluación II Término 2011-2012. 1/Diciembre/2011. TELG1001

Tema 1. (30 puntos) Un estudiante de la materia Sistemas Lineales ha determinado que un sistema LTI-DT está integrado por la conexión serie-paralelo de cuatro subsistemas, tal como se muestra en la figura.

Conociendo que:

h_1 [n] = \mu [n] h_2 [n] = \mu [n+2] h_3 [n] = \delta [n-2] h_4 [n] = \alpha_1^n \mu [n]

a. Encontrar la respuesta impulso del sistema completo, es decir h[n], indicando si el sistema integral es FIR o IIR.

b. Determinar, justificando su respuesta, si el sistema es BIBO estable. Comente además sobre la causalidad del mismo.

c. Hallar la respuesta y[n], en forma de mínima expresión, frente a la entrada

x[n] = \alpha_2^n \mu [n]

d. Determinar el valor de y[0] si acaso α1 = 0.20 y α2 = 0.40

Coordinador: Tama Alberto

Publicado el

1Eva2010TI_T4 LTI DT bloques y respuesta impulso

1ra Evaluación I Término 2010-2011. 8/Julio/2010. TELG1001

Tema 4. (25 puntos) Un estudiante de Sistemas Lineales ha encontrado que un determinado sitema LTI-DT causal, en el dominio del tiempo, tiene la siguiente representación:

Determinar:

a. La respuesta impulso h[n]

b. La respuesta y[n] frente a la siguiente excitación:

x[n] = e^{-0.25 n} \mu [n] - e^{-0.50 n} \mu [n]

c. ¿Es el sistema BIBO estable?, justifique su respuesta.

Publicado el

1Eva2012TI_T1 LTI CT Polos y ceros de H(s) con respuesta DC conocida

1ra Evaluación I Término 2012-2013. 5/julio/2012. TELG1001

Tema 1. (30 puntos) El diagrama de polos y ceros de un sistema de segundo orden cuya función de transferencia H(s) es mostrado en la siguiente figura, donde se conoce que la respuesta DC de este sistema es -1. es decir H(j0)=-1.

a. Conociendo el hecho que:

H(s) = \frac{k (s^2 + b_1 s + b_2)}{s^2 + a_1 s + a_2}

determinar el valor de las constantes k, b1,b2, a1 y a2.

b. Encontrar la respuesta impulso h(t) del mencionado sistema.

c. Comente justificadamente acerca de la estabilidad interna y externa del mencionado sistema.

Publicado el

1Eva2010TI_T3 LTI DT subsistemas serie y respuesta impulso

1ra Evaluación I Término 2010-2011. 8/Julio/2010. TELG1001

Tema 3. (25 puntos) El sistema que se muestra en la siguiente figura es el resultante de la combinación de dos subsistemas conectados en cascada.

Determinar:

a. las respuestas impulso de cada subsistema y del sistema completo, es decir h1[n], h2[n], h[n].

h1[n]
h2[n]
h[n]

b. su respuesta y[n], en forma de mínima expresión, frente a la siguiente excitación:

x[n] = e^{-0.5n} \mu [n]
Publicado el

1Eva2010TI_T2 LTI CT diagrama de bloques para H(s)

1ra Evaluación I Término 2010-2011. 8/Julio/2010. TELG1001

Tema 2. (25 puntos) Considere la existencia de un sistema, cuyo esquema del diagrama de bloques en el dominio de la frecuencia compleja, que relaciona la entrada-salida del mismo, es el siguiente:

Determinar:

a. La función de transferencia H(s) del mencionado sistema y esquematizar en el plano complejo los polos y ceros. Comente sobre la estabilidad de este sistema, justificando su respuesta.

b. La respuesta impulso h(t) de dicho sistema, y la obtención de su valor inicial y final a partir de la aplicación del TVI y TVF.

c. La ecuación diferencial de coeficientes constantes que representa al referido sistema.

d. La respusta que se obtendría si la exitación es:

x(t) = e^{-3t} \mu(t)
Publicado el

1Eva2010TI_T1 LTI CT respuesta estado cero desde dx(t)/dt

1ra Evaluación I Término 2010-2011. 8/Julio/2010. TELG1001

Tema 1. (25 puntos) Un estudiante de la materia Sistemas Lineales, ha determinado que la representación esquemática de la respuesta impulso h(t), de un sistema LTI-CT es aquella que se muestra en la siguiente figura.

Si se conoce la derivada de la entrada de dicho sistema, esto es dx(t)/dt, determine y esquematice su respuesta de estado cero, es decir:

y(t) = x(t)⊗h(t)

Publicado el

1Eva2010TII_T4 LTI DT h[n] respuesta a impulso

1ra Evaluación II Término 2010-2011. 9/Diciembre/2010. TELG1001

Tema 4. (25 puntos) Un estudiante de la materia Sistemas Lineales ha determinado que una de las raíces características del sistema LTI-DT causal, que se muestra en la siguiente figura, es γ=1/4. La ecuación de diferencias que relaciona la entrada-salida del mismo es dada por:

y[n] - \frac{5}{4} y[n-1] + \frac{1}{36} y[n-2] + \frac{1}{18} y[n-3] = x[n] - \frac{1}{2} x[n-1]

Determinar:

a. La respuesta impulso h[n] del sistema. Su respuesta debe ser de la forma:

h[n] = a \alpha ^n \mu [n] + b \beta ^n \mu [n] + x \rho ^n \mu [n]
a = b = c =
α = β = ρ =

obtenga los valores pertinentes-

b. ¿Es el sistema BIBO estable?, justifique su respuesta