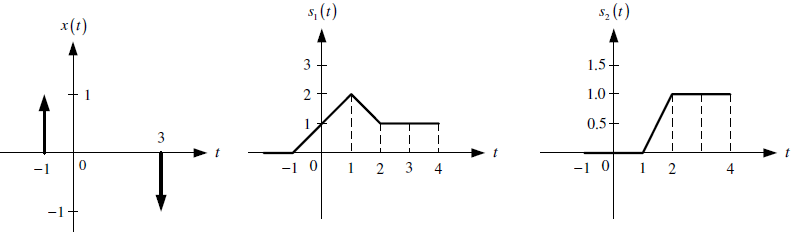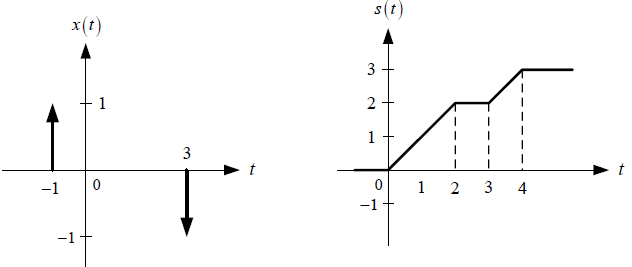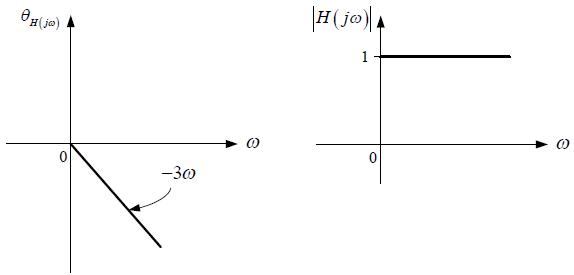Publicado en

1Eva2014TI_T1 LTI CT subsistemas en serie

1ra Evaluación I Término 2014-2015. 3/Julio/2014. TELG1001

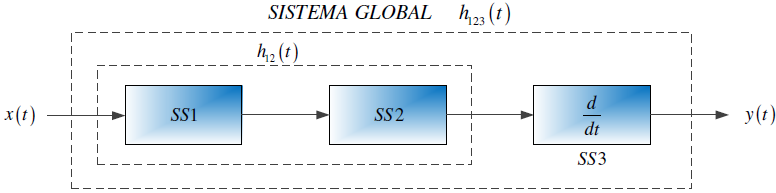
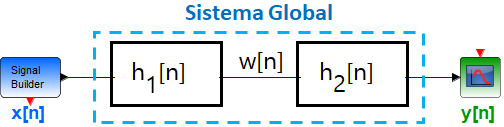
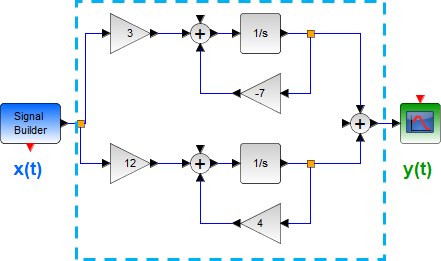
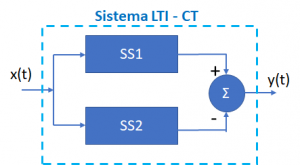
Tema 1. (35 puntos) Para el sistema global, integrado por la conexión en serie de tres subsistemas:

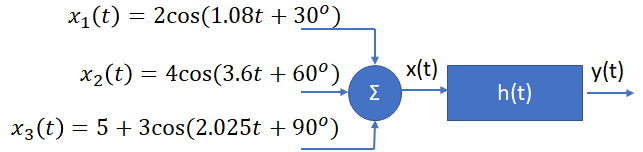
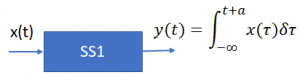
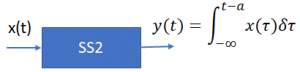
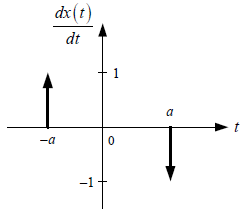
Y, conociento la exitación x(t) y las respuestas de paso s(t) de los subsistemas SS1 y SS2.

Se le ha solicitado lo siguiente:

a. Determinar, esquematizar y etiquetar la respuesta impulso equivalente entre los subsistemas SS1 y SS2, es decir h12(t).

b. Determinar, esquematizar y etiquetar la respuesta impulso equivalente del sistema global, es decir h123(t).

c. Haciendo la debida justificación, encierre en un círculo, en la tabla que se muestra a continuación, la respuesta correcta.

d. Determinar, esquematizar y etiquetar la salida y(t).

e. Obtener el valor de la energía contenida en la señal de salida y(t)

literal b
Sistema SS1 Sistema SS2 Equivalente
SS1 y SS2		 SISTEMA GLOBAL
CON MEMORIA Si No Si No Si No Si No
CAUSAL Si No Si No Si No Si No
BIBO ESTABLE Si No Si No Si No Si No

Coordinador: Tama Alberto

Publicado en

1Eva2012TII_T4 LTI CT bloques en paralelo-serie con Laplace

1ra Evaluación II Término 2012-2013. 29/Noviembre/2012. TELG1001

Tema 4. (25 puntos) Considere la existencia de un sistema LTI-CT cuya representación mediante diagrama de bloques en el dominio de la frecuencia compleja, que relaciona la entrada-salida del mismo, es la siguiente:

Adicionalmente, la Región de Convergencia de la función de transferencia del referido sistema es -7<Re(s)<4.

Determinar:

a. La función de transferencia H(s) del mencionado sistema y esquematizar su diagramas de polos y ceros en el plano complejo.

b. La respuesta impulso h(t). Comente sobre la estabilidad de éste sistema, justificando debidamente su respuesta.

c. La representación del mencionado sistema (en el dominio de tiempo contínuo) mediante diagrama de bloques.

d. La respuesta de dicho sistema frente a la entrada

x(t) = e^{-5t} \mu (t)

Referencia: 1Eva2016TII_T2 LTIC bloques en paralelo-serie con Laplace, 1Eva2011TII_T3 LTI CT H(s) desde expresión con operadores D

Coordinador: Tama Alberto

Publicado en

1Eva2012TII_T3 LTI CT subsistemas en serie

1ra Evaluación II Término 2012-2013. 29/Noviembre/2012. TELG1001

Tema 2. (25 puntos) Para el sistema global integrado por la conexión en serie de tres subsistemas,

Y, conociendo la entrada o excitación x(t) junto con la respuesta de paso s(t) para el segundo subsistema, se le ha solicitado:

a. Determinar, esquematizar y etiquetar la respuesta w(t) que se genera a la salida del segundo subsistema LTI-CT, así como su correspondiente energía.

b. Indique justificadamente si el segundo subsistema es BIBO estable o no.

c. Mediante la aplicación de la propiedad de la derivación, obtener la transformada de Laplace de la señal w(t), esto es W(s).

d. Determinar, estquematizar y etiquetar la salida y(t)

e. Encontrar la relación entre las energías de la señal de salida y(t) a la señal de entrada x(t).

Publicado en

1Eva2012TII_T2 LTI DT en serie

1ra Evaluación II Término 2012-2013. 29/Noviembre/2012. TELG1001

Tema 2. (25 puntos) Dos sistemas LTI-DT causales, tienen respuesta impulso h1[n] y h2[n] respectivamente. Los sistemas en referencia, utilizados como subsistemas, son conectados en cascada con la finalidad de conformar un sistema global, tal como se muestra en la siguiente figura.

Las ecuaciones de diferencia que relacionan a cada sistema y al global son las siguientes:

S1: w[n] = \frac{1}{2}w[n-1] + x[n] S2: y[n] = \alpha y[n-1] + \beta w[n] SG: y[n] = -\frac{1}{8}y[n-2] + \frac{3}{4}y[n-1] + x[n]

a. Determinar los valores de α y β.

b. Obtener la respuesta impulso del sistema global e indicar a que tipo de sistema pertenece (FIR o IIR)

c. Comente acerca de la estabilidad interna y externa del sistema global. Justifique su respuesta

d. Determinar y esquematizar la respuesta de paso del sistema global.

Coordinador: Tama Alberto

Publicado en

1Eva2012TII_T1 LTI CT entradas periódicas superpuestas jω

1ra Evaluación II Término 2012-2013. 29/Noviembre/2012. TELG1001

Tema 1. (25 puntos) Un estudiante de la materia Sistemas Lineales ha determinado que la señal de entrada a un sistema LTI-CT es la superposición de 3 señales periódicas. Las señales se muestran en la figura:

Conociendo además que la respuesta de frecuencia del referido sistema es la siguiente:

a. Comprobar justificadamente si la señal de entrada x(t) es periódica o no periódica. Si su respuesta es afirmativa, encuentre entonces el periodo fundamental de la misma.

b. Determinar, esquematizar y etiquetar la respuesta de impulso h(t).

c. Indicar, justificando su respuesta, si el referido sistema es con memoria o sin memoria, causal o no causal. BIBO estable o no.

d. Encontrar la relación entre las potencias de la señal de salida y(t) a la señal de entrada x(t)

Publicado en

1Eva2012TI_T3 LTI CT subsistemas en serie

1ra Evaluación I Término 2012-2013. 5/julio/2012. TELG1001

Tema 3. (40 puntos) Para el sistema global integrado por la conexión en serie de tres subsistemas, y conociendo la entrada o excitación x(t) junto con la respuesta de paso s(t) para el segundo subsistema se requiere:

a. Determinar, esquematizar y etiquetar la respuesta w(t) que se genera a la salida del segundo subsistema LTI-CT, asi como su correspondiente energía.

b. Indique justificadamente si el segundo subsistema es BIBO estable o no.

c. Obtener, esquematizar y etiquetar la salida y(t) que genera el sistema global, asi como su correspondiente energía.

 

Publicado en

1Eva2012TI_T2 LTI DT en serie

1ra Evaluación I Término 2012-2013. 5/julio/2012. TELG1001

Tema 2. (30 puntos) Dos sistemas LTI-DT tienen respuesta impulso h1[n] y h2[n] respectivamente. Los sistemas en referencia, utilizados como subsistemas, son conectados en cascada con la finalidad de conformar un sistema total, tal como se muestra en la siguiente figura.

h_1 [n] = (0.8)^n \mu [n] - 0.3 (0.8)^{n-1} \mu [n-1] h_2 [n] = (0.3)^n \mu [n] - 0.8 (0.3)^{n-1} \mu [n-1]

a. Determinar la respuesta impulso del sistema total e indicar a qué tipo de sistema pertenece (FIR o IIR).

b. Justificando su respuesta, indique si el sistema es BIBO estable o no.

c. Determinar y esquematizar la respuesta de dicho sistema, conociendo que:

x[n] = \delta [n] - \delta [n-1]

Coordinador: Tama Alberto

Publicado en

1Eva2012TI_T1 LTI CT Polos y ceros de H(s) con respuesta DC conocida

1ra Evaluación I Término 2012-2013. 5/julio/2012. TELG1001

Tema 1. (30 puntos) El diagrama de polos y ceros de un sistema de segundo orden cuya función de transferencia H(s) es mostrado en la siguiente figura, donde se conoce que la respuesta DC de este sistema es -1. es decir H(j0)=-1.

a. Conociendo el hecho que:

H(s) = \frac{k (s^2 + b_1 s + b_2)}{s^2 + a_1 s + a_2}

determinar el valor de las constantes k, b1,b2, a1 y a2.

b. Encontrar la respuesta impulso h(t) del mencionado sistema.

c. Comente justificadamente acerca de la estabilidad interna y externa del mencionado sistema.

Publicado en

1Eva2011TII_T3 LTI CT H(s) desde expresión con operadores D

1ra Evaluación II Término 2011-2012. 1/Diciembre/2011. TELG1001

Tema 2. (40 puntos) Considere la existencia de un sistema LTI-CT, cuya representación mediante el uso de operadores es la siguiente:

(D^2 + 3 D -28) y(t) = (15D+72) x(t)

Adicionalmente, se conoce que la Región de Convergencia de la función de transferencia del referido sistema es -7 < Re(s) < 4.

Determinar,

a. La función de transferencia H(s) y esquematizar en el plano complejo su diagrama de polos y ceros. Comente sobre la estabilidad del sistema, justificando debidamente su respuesta.

b. La respuesta impulso h(t) de dicho sistema, y la obtención de su valor inicial y final a partir de la aplicación del TVI y TVF.

c. La representación del mencionado sistema, en el dominio de tiempo contínuo, mediante diagrama de bloques.

d. La respuesta de dicho sistema frente a la entrada:

x(t) = e^{-5t} \mu (t)

Referencia: 1Eva2016TII_T2 LTI CT bloques en paralelo-serie con Laplace ,  1Eva2012TII_T4 LTI CT bloques en paralelo-serie con Laplace

Publicado en

1Eva2011TII_T2 LTI CT Respuestas de subsistemas en serie

1ra Evaluación II Término 2011-2012. 1/Diciembre/2011. TELG1001

Tema 2. (30 puntos) Para el sistema LTI_CT integrado por la conexión en serie de dos subsistemas; y conociendo la señal de entrada x(t) junto a la respuesta impulso h(t) para el primer subsistema, se requiere:

a. Determinar, esquematizar y etiquetar la respuesta w(t) que se genera a la salida del primer subsistema, asi como su correspondiente energía.

b. Obtener, esquematizar y etiquetar la salida y(t) que genera el sistema global, así como su correspondiente energía.

c. Conociendo la existencia de la señal z(t), expresar w(t) como una función de  z(t).