[ concepto ] [ retraso ] [ adelanto ] [ amplitud ] [ inversión ] [ algoritmo ]
Referencia: Lathi 1.7-4 p104, Oppenheim 1.6.3 p46
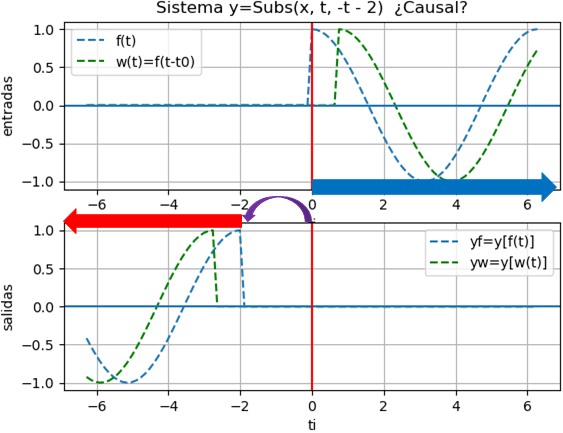
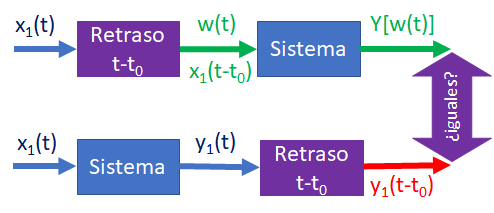
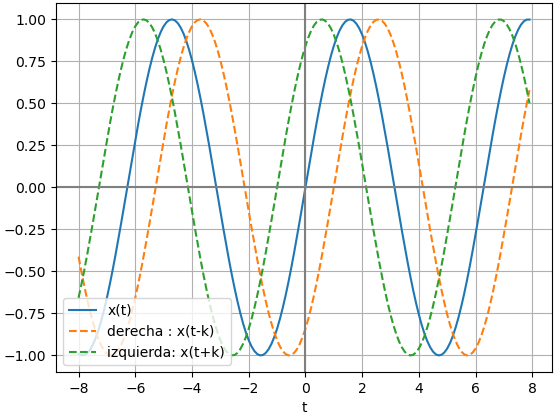
Un sistema es CAUSAL (no-anticipativo o físico) si la salida y(t) en un valor arbitrario de tiempo t=t0 depende solo de la entrada x(t) para t ≤ t0 , es decir depende solo de los valores presentes y/o pasados de la entrada; no depende de valores futuros. 
No es posible obtener una salida antes que se aplique la entrada.
[ concepto ] [ retraso ] [ adelanto ] [ amplitud ] [ inversión ] [ algoritmo ]
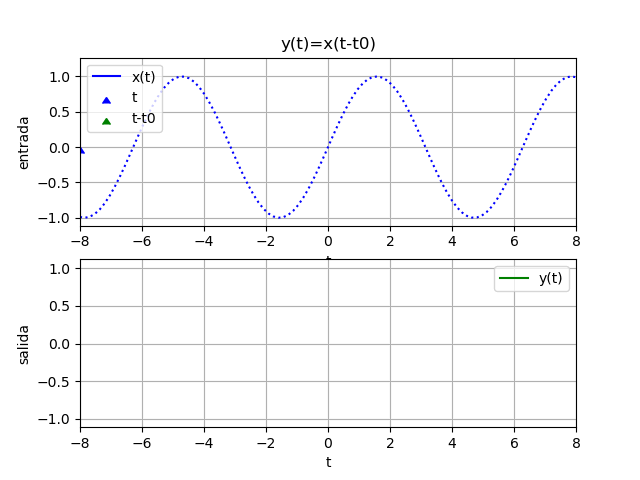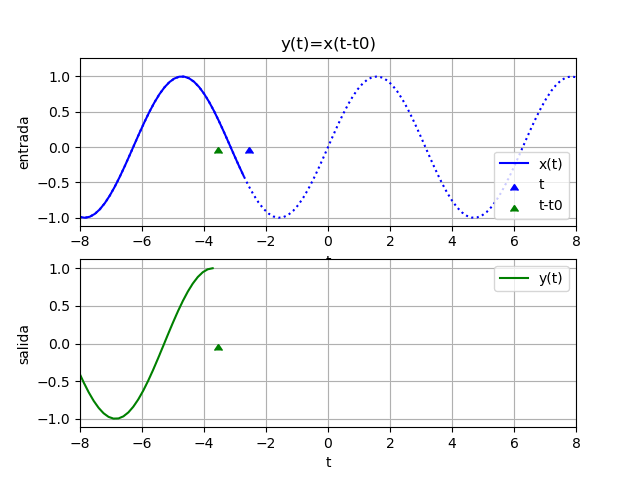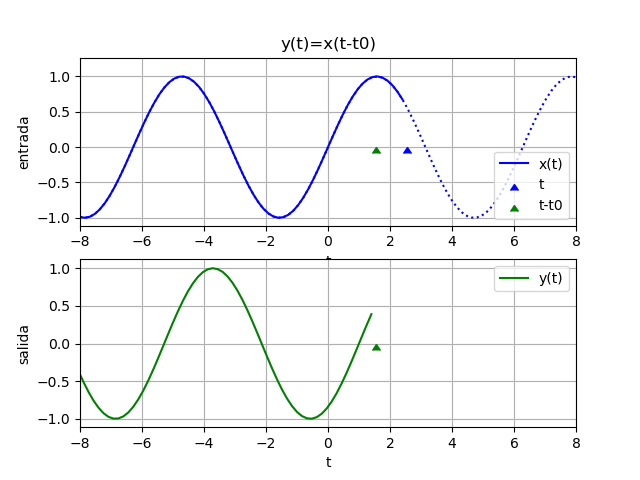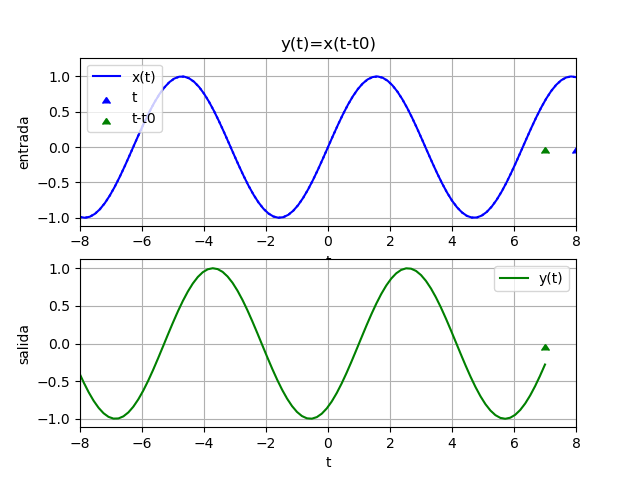
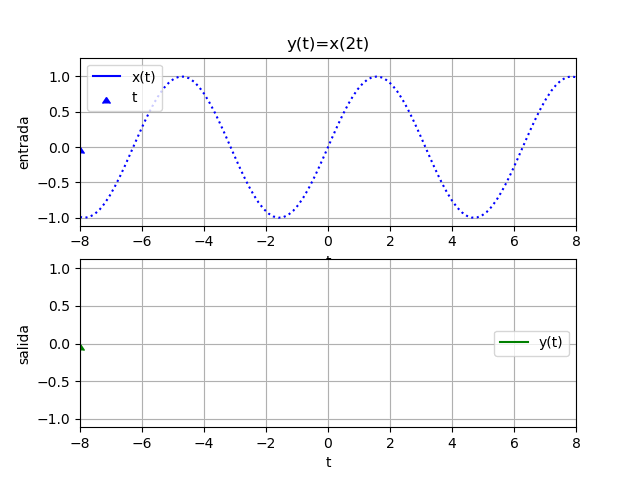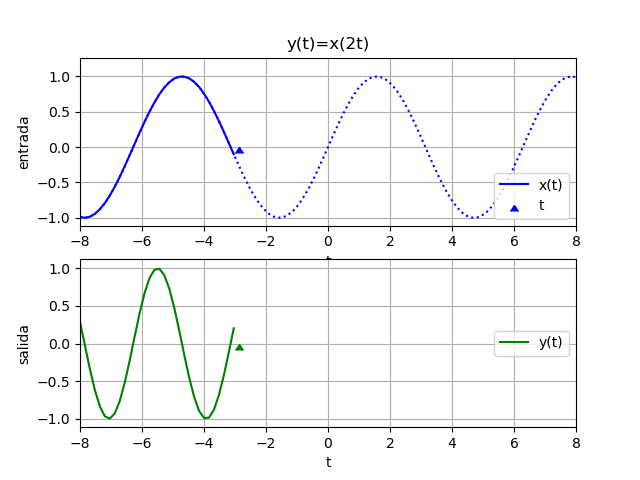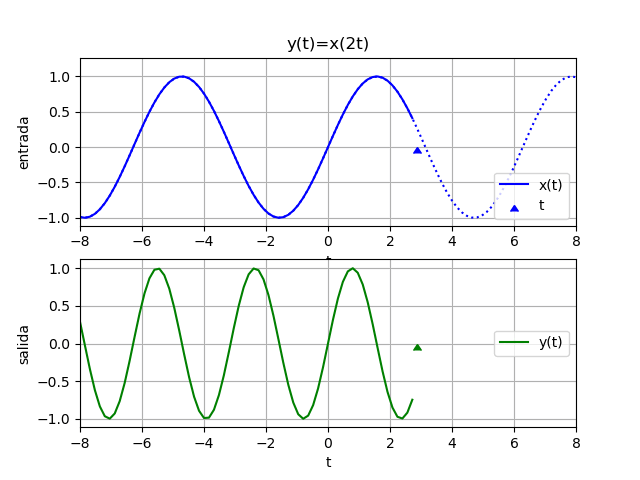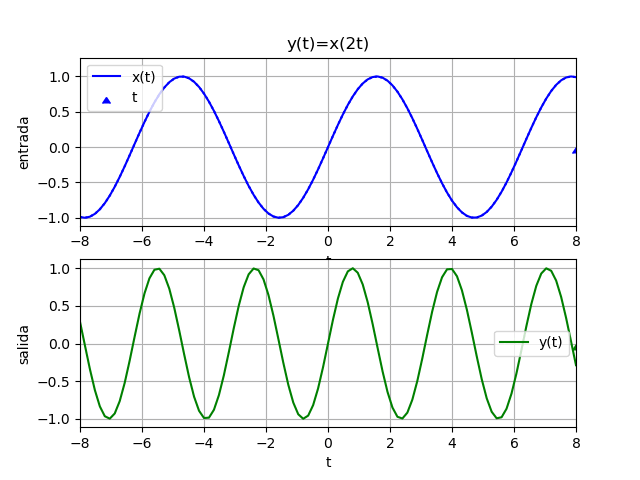
Ejemplos 1. desplazamiento en tiempo, retraso
Referencia: Hsu 1.5.D p17
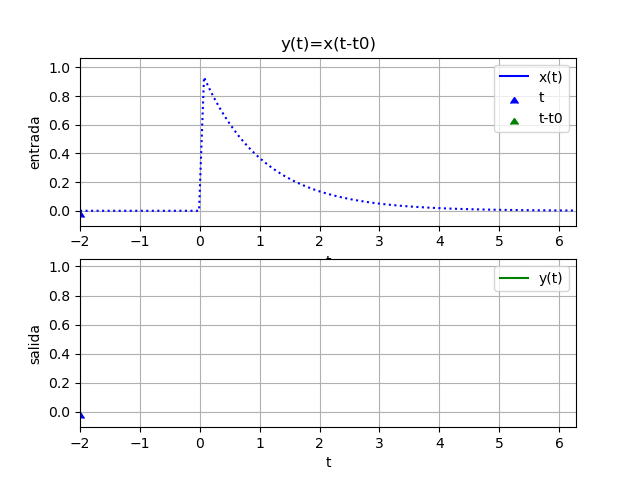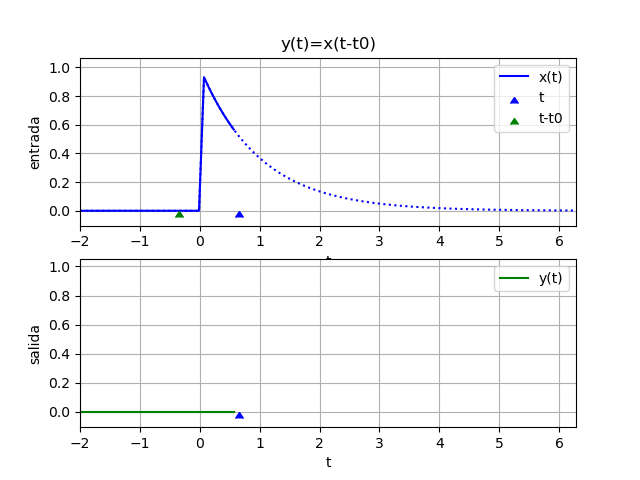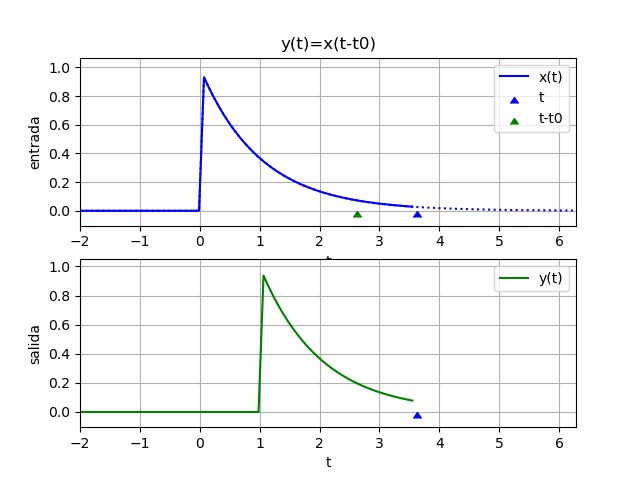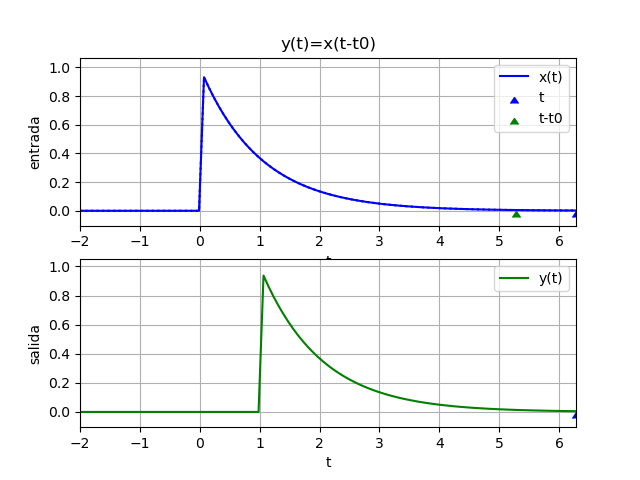
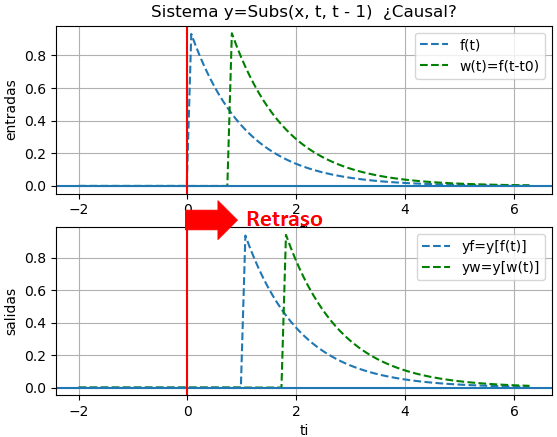
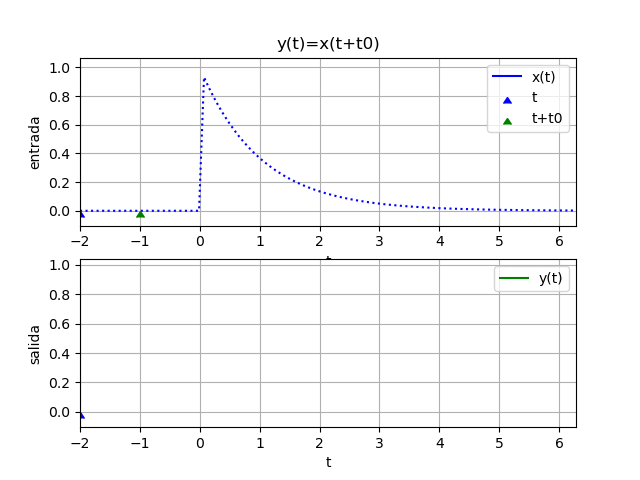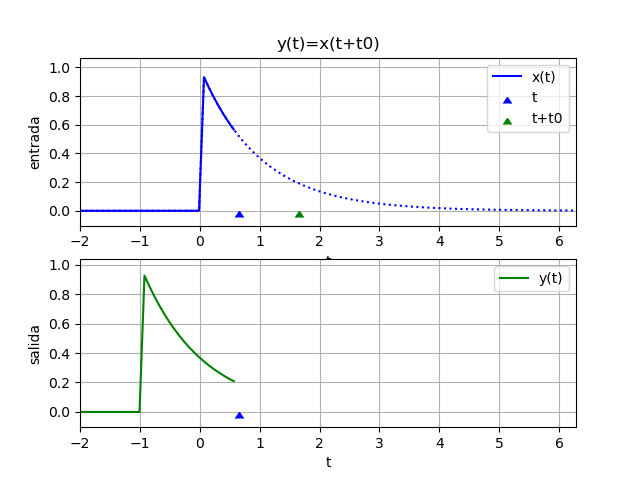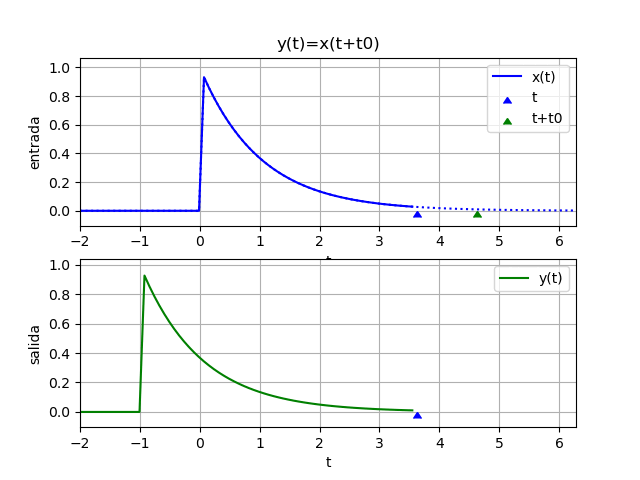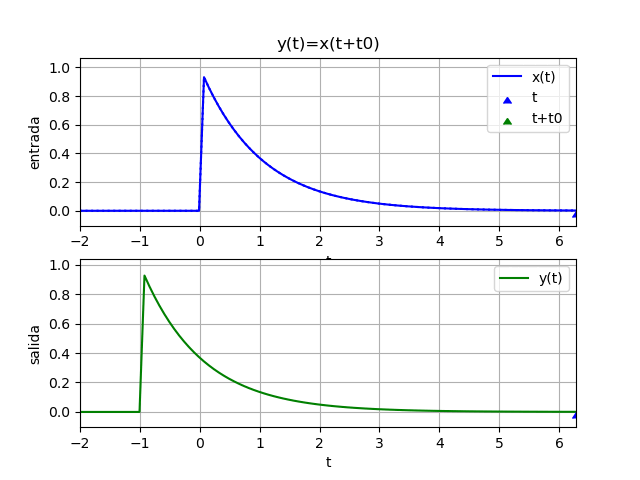
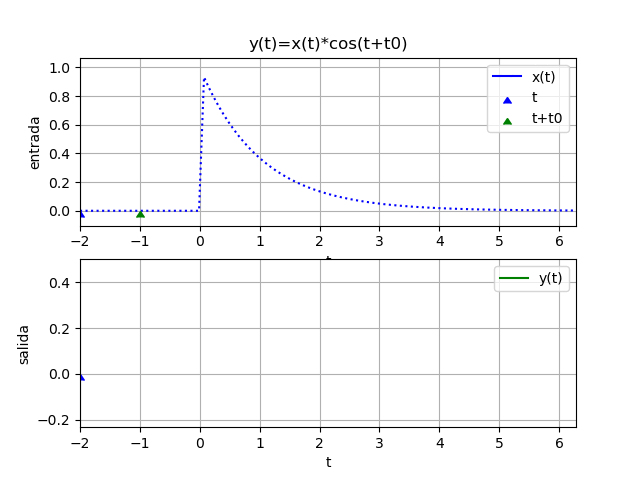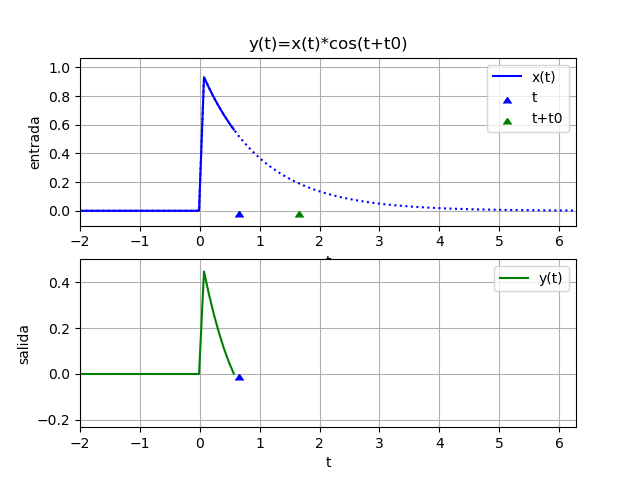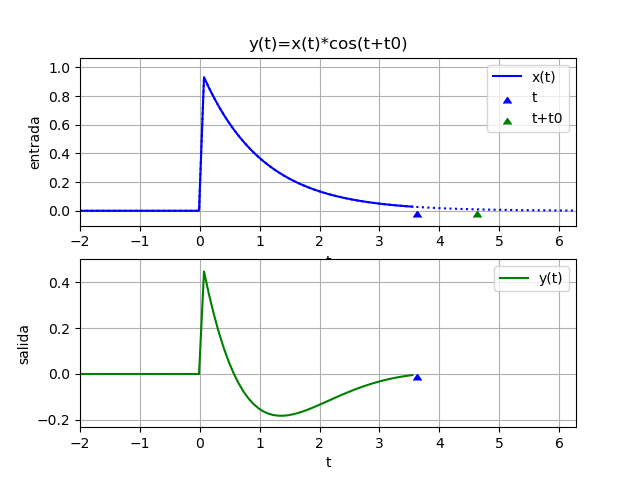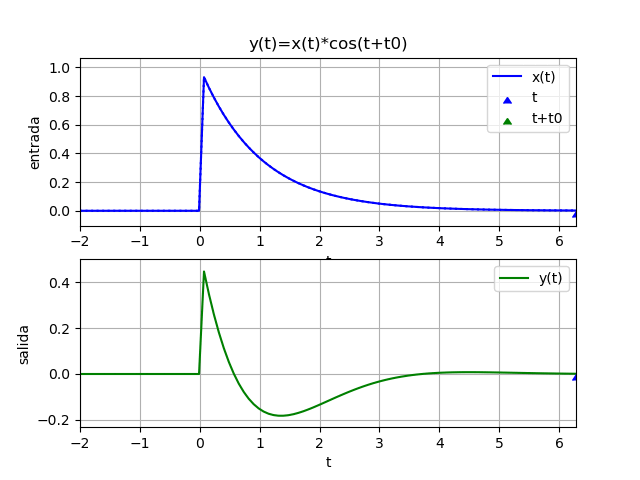
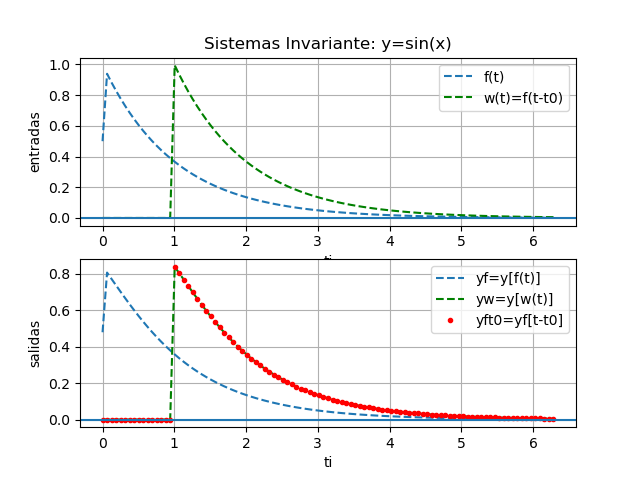
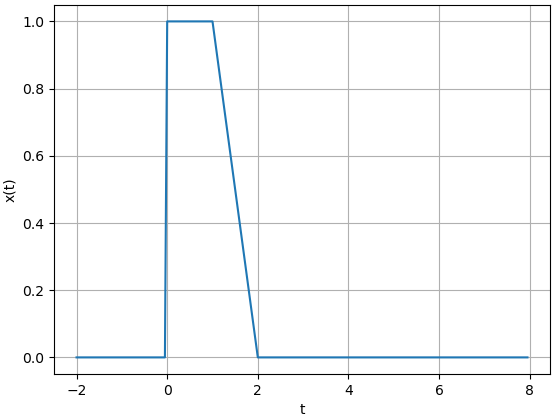
y(t) = x(t - 1)Para observar mejor el sistema del ejemplo, se inicia con un desplazamiento negativo. Si t es en segundos, la salida depende de los valores de x hace un segundo atrás (t-1)
Usando como entrada:
x(t) = e^{-t} \mu (t) 1 - t
yf = e *Heaviside(t - 1)
1 - t
yw = 2.11700001661267*e *Heaviside(t - 1.75)
Considere los eventos de interés mundial que se transmiten con un retraso de segundos para corregir "fallos" o por seguridad, se puede aún editar lo que los espectadores en televisión pueden observar, en tiempo "casi real"
Por ejemplo:
" La cadena de televisión NBC transmitirá la ceremonia de apertura de los Juegos Olímpicos de Río de Janeiro 2016 con una hora de retraso ... eso permitirá a los productores "curar" la cobertura para proporcionar un contexto adecuado."
12-Julio-2016
"In radio and television, broadcast delay is an intentional delay when broadcasting live material. Such a delay may be short (often seven seconds) to prevent mistakes or unacceptable content from being broadcast."
https://en.wikipedia.org/wiki/Broadcast_delay
En el caso contrario, los sistemas NO CAUSALES muestran una salida anticipada a la señal de entrada. ¿es posible? ¿cómo?
[ concepto ] [ retraso ] [ adelanto ] [ amplitud ] [ inversión ] [ algoritmo ]
Ejemplo 2. desplazamiento en tiempo, adelanto
Referencia: Hsu 1.5.D p17
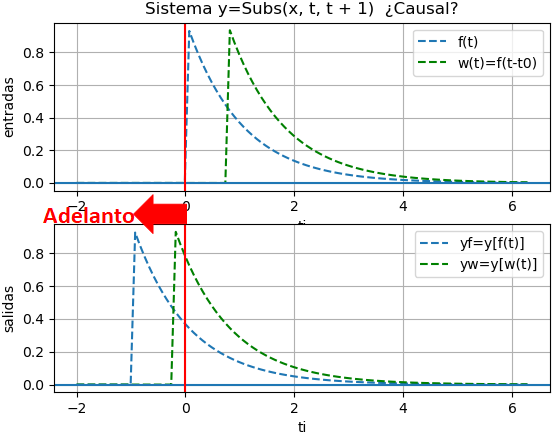
y(t) = x(t + 1)si t es en minutos o años, la salida depende de los valores que x(t) tendría un minuto o año después o (t+1).
Si t es en días, la situación se vuelve complicada de realizar, es como decir: para determinar el valor de la variable y(t) HOY, necesitamos conocer el valor de x(t+1) que es MAÑANA.
Los sistemas no-casuales por tener variable independiente referenciada a tiempo futuro, no se pueden implementar en tiempo real. Sin embargo si los sistemas no causales se realizan con variables diferentes al tiempo, por ejemplo "espacio" se podrían implementar.
Usando como entrada, la misma que el ejemplo anterior
x(t) = e^{-t} \mu (t) -t - 1
yf = e *Heaviside(t + 1)
-t - 1
yw = 2.11700001661267*e *Heaviside(t + 0.25)
Aunque si considera que los datos de tiempo registrado para un evento, el análisis se puede realizar en un rango donde los no-causales aún se podrían analizar o procesar aunque no en tiempo real.
"No, la lluvia no hace que te duelan las rodillas" - AS.com. 25-feb-2017. https://as.com/deporteyvida/2017/02/25/portada/1488041024_696949.html
[ concepto ] [ retraso ] [ adelanto ] [ amplitud ] [ inversión ] [ algoritmo ]
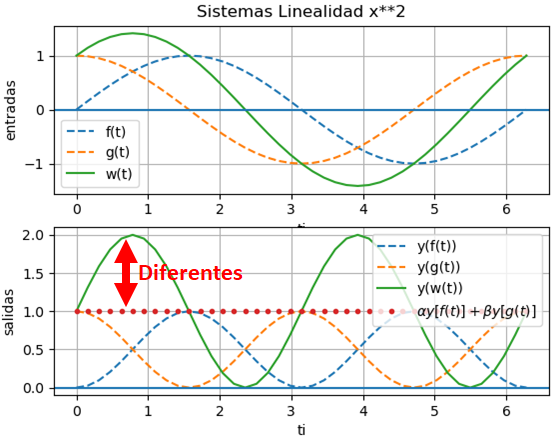
Ejemplo 3. Sistema con amplitud variable en tiempo (AM)
Referencia: Oppenheim Ejemplo 1.12 p47
Considere el sistema dado por:
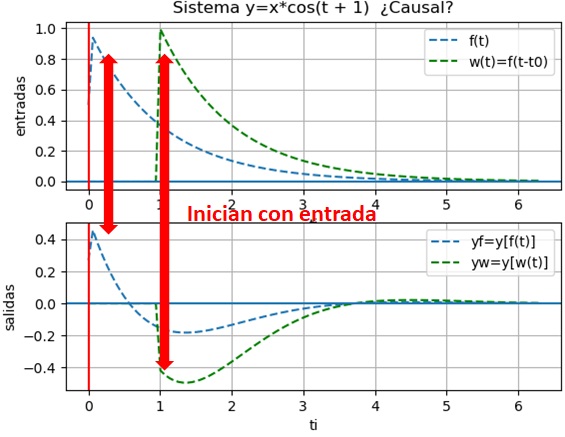
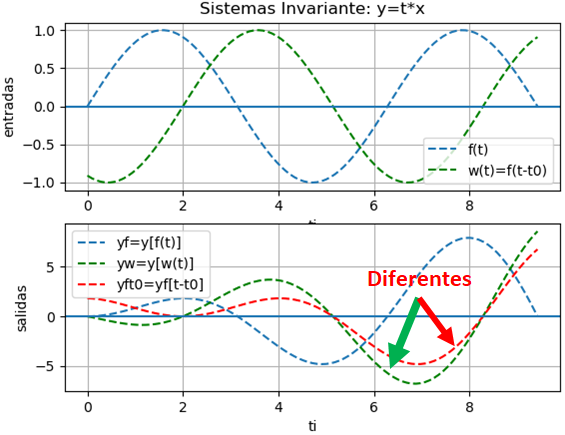
y(t) = x(t) \cos(t+1)En este sistema, la salida en cualquier tiempo t es igual a la entrada en el mismo tiempo t multiplicada por un número que varia en el tiempo. Usando q(t) = cos(t+1) que es una función variante en el tiempo, el sistema puede escribirse como
y(t) = x(t) q(t)Se observa que solo el valor actual de la entrada x(t) influye en el valor de salida de y(t). Se concluye que el sistema es causal y también sin memoria.
x(t) = e^{-t} \mu (t)resultados con algoritmo:
-t
yf = e *cos(t + 1)*Heaviside(t)
-t
yw = 2.71828182845905*e *cos(t + 1)*Heaviside(t - 1.0)
[ concepto ] [ retraso ] [ adelanto ] [ amplitud ] [ inversión ] [ algoritmo ]
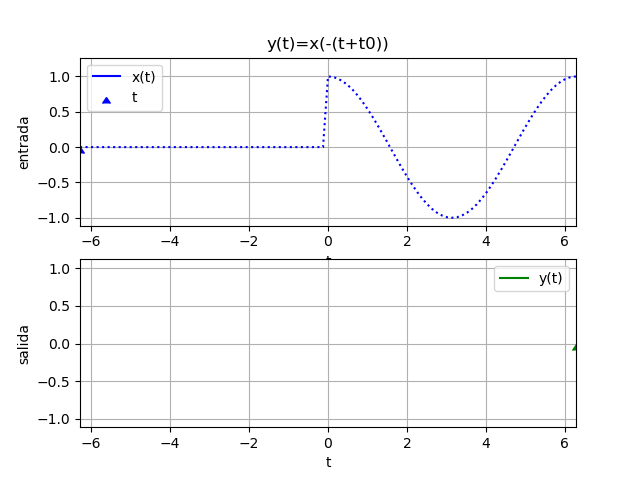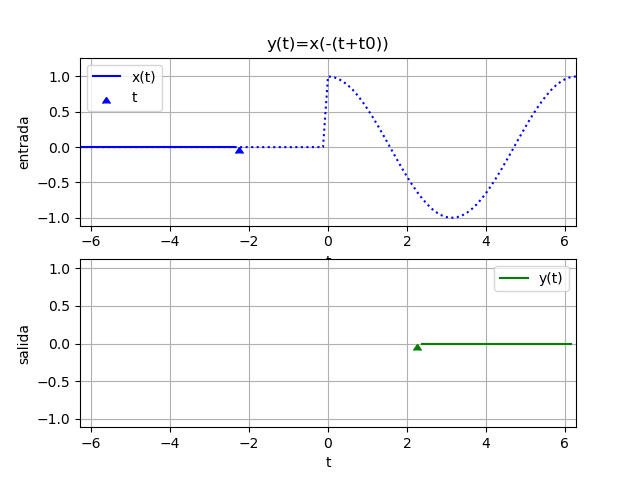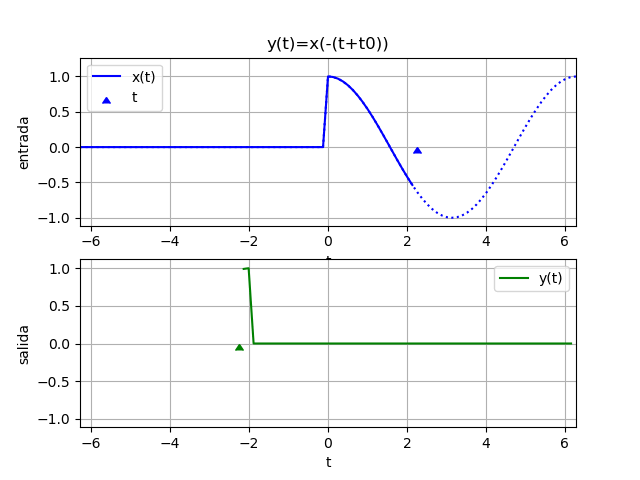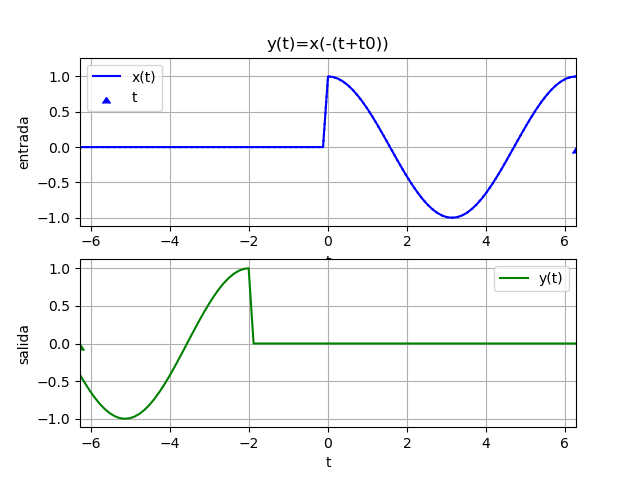
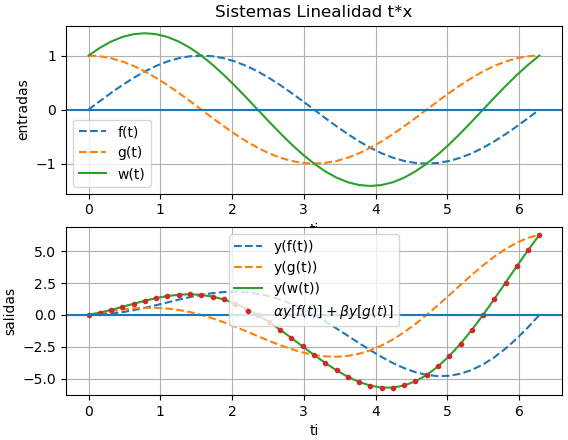
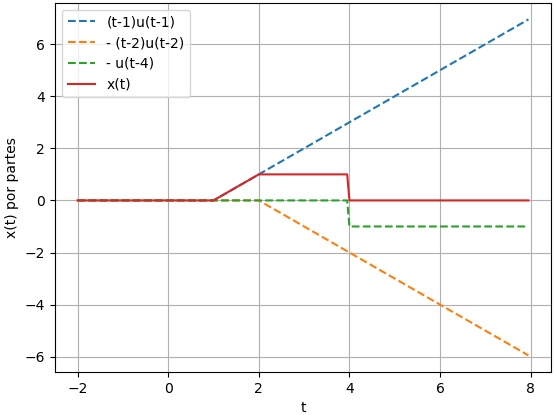
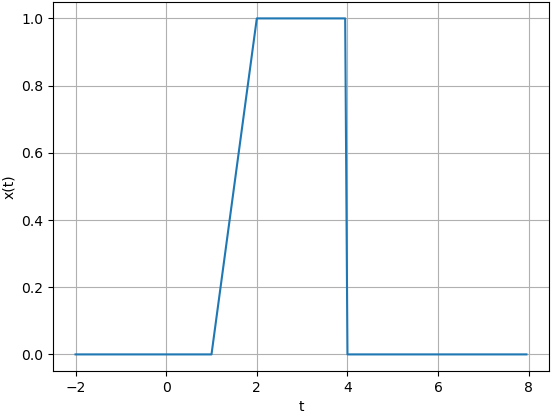
Ejemplo 4. Adelanto e Inversión en tiempo
y(t) = x(-(t+2))
Suponga que x(t) = cos(t) μ(t) para hacer notar el inicio de la señal de entrada
[ concepto ] [ retraso ] [ adelanto ] [ amplitud ] [ inversión ] [ algoritmo ]
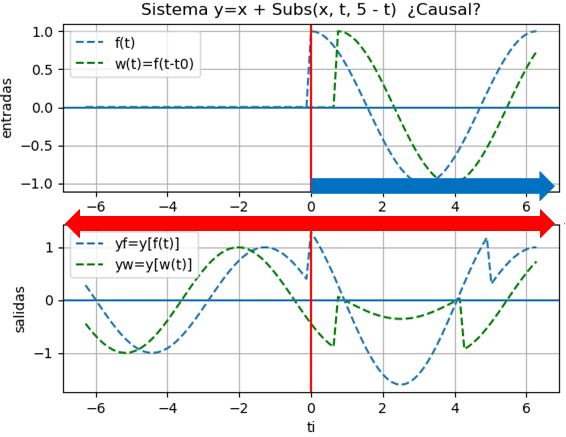
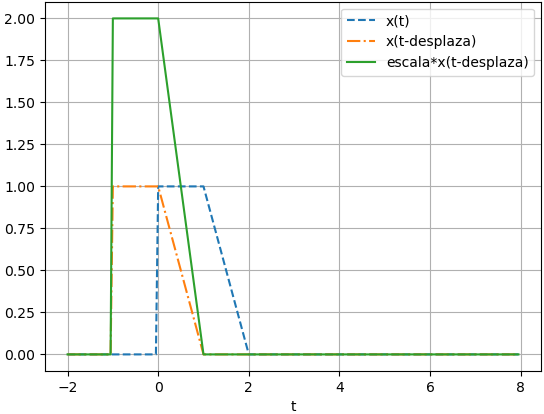
Ejemplo 5. desplazamiento e inversión en tiempo
y(t) = x(t)+x(5-t)
Suponga que x(t) = cos(t) μ(t) para hacer notar el inicio de la señal de entrada
Usando como entrada
x(t) = \cos(t) \mu (t)yf = cos(t)*Heaviside(t) + cos(t - 5)*Heaviside(5 - t) yw = cos(t - 4.25)*Heaviside(4.25 - t) + cos(t - 0.75)*Heaviside(t - 0.75)
Descripción a ser aplicada a TeneT:
Ejercicios:
a) y(t) = x(t-1)
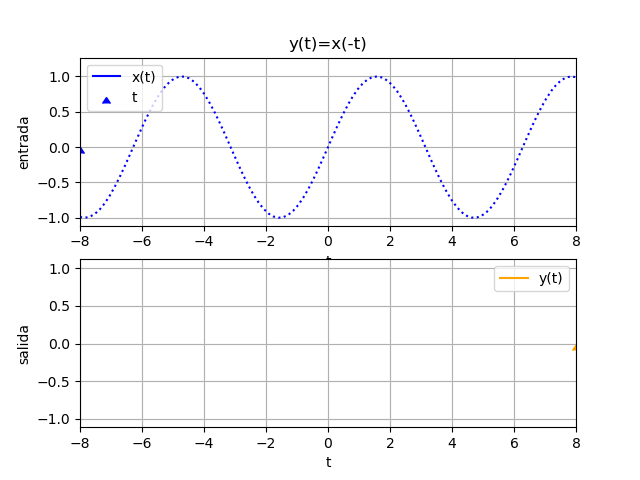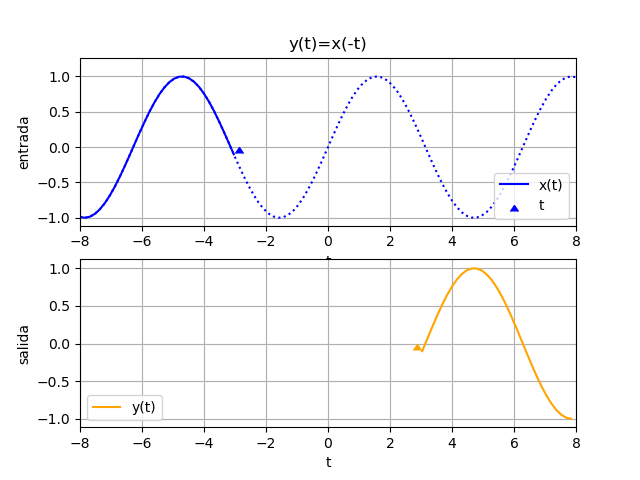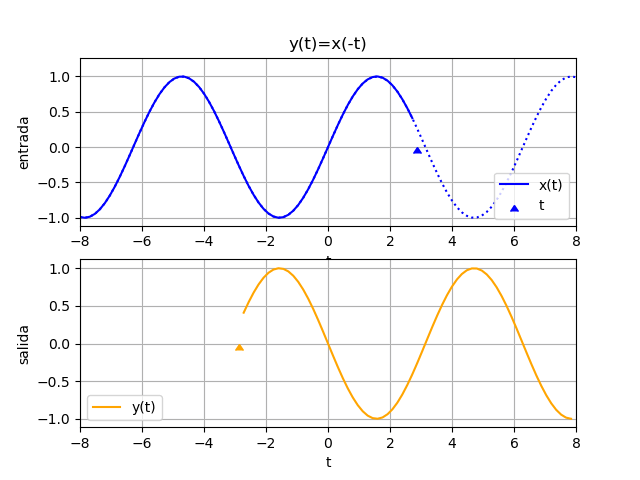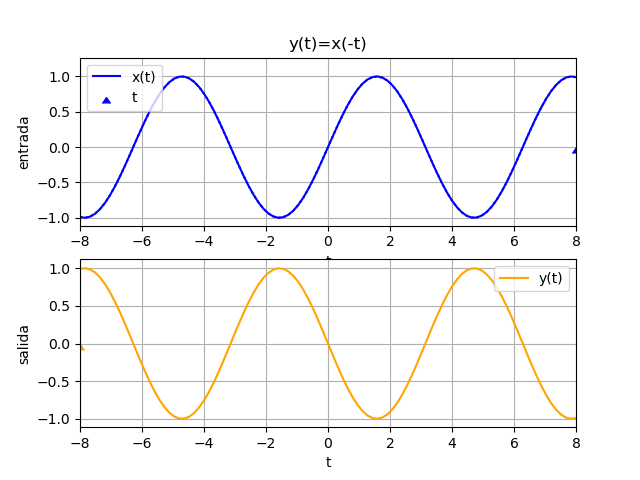
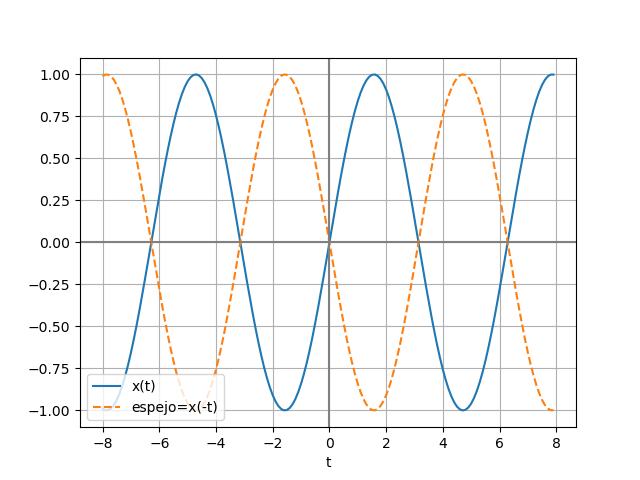
b) y(t) = x(-t)
c) y(t) = x(t)+x(5-t)
d) otra
[ concepto ] [ retraso ] [ adelanto ] [ amplitud ] [ inversión ] [ algoritmo ]
Algoritmo en Python
Ejemplo 1. desplazamiento en tiempo, retraso
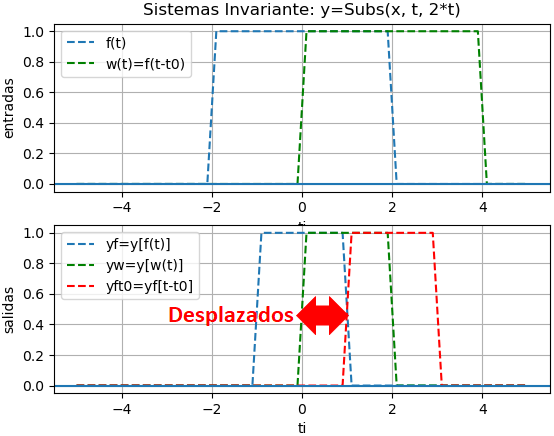
El sistema se aplica sustituyendo la variable t por t-1 en la entrada x, con la instrucción y = sym.Subs(x,t,t-1,evaluate=False)
# entradas desplazadas en t, revisar salida # Sistemas Causales y NO causales en tiempo # Hsu 1.5.D p17 import numpy as np import sympy as sym import matplotlib.pyplot as plt equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, 'numpy'] # INGRESO t = sym.Symbol('t', real=True) x = sym.Symbol('x', real=True) t0 = 0.75 # señales de entrada f = sym.exp(-t)*sym.Heaviside(t) w = f.subs(t,t-t0) # sistema y = sym.Subs(x,t,t-t0,evaluate=False) # intervalo de t[a,b] para graficar a = 0 b = 2*np.pi muestras = 101 # PROCEDIMIENTO # Sistema sobre señal de entrada yf = y.subs(x,f).doit() yw = y.subs(x,w).doit() # Para gráfica ti = np.linspace(a,b,muestras) # señales de entrada ft = sym.lambdify(t,f) wt = sym.lambdify(t,w) # señales de salida yft = sym.lambdify(t,yf,modules=equivalentes) ywt = sym.lambdify(t,yw,modules=equivalentes) # evalua entradas ti fi = ft(ti) wi = wt(ti) # evalua salidas ti yfi = yft(ti) ywi = ywt(ti) # SALIDA print('yf:') sym.pprint(yf) print('yw:') sym.pprint(yw) # grafica plt.subplot(211) # entradas plt.plot(ti,fi,'--', label='f(t)') plt.plot(ti,wi,'--',color='green', label='w(t)=f(t-t0)') plt.axhline(0) plt.axvline(0,color='red') plt.xlabel('ti') plt.ylabel('entradas') plt.title('Sistema y='+str(y)+ ' ¿Causal?') plt.legend() plt.grid() plt.subplot(212) # salidas plt.plot(ti,yfi,'--',label='yf=y[f(t)]') plt.plot(ti,ywi,'--',color='green', label='yw=y[w(t)]') plt.axhline(0) plt.axvline(0,color='red') plt.xlabel('ti') plt.ylabel('salidas') plt.legend() plt.grid() plt.show()
Ejemplo 2. desplazamiento en tiempo, adelanto
lo mismo que el anterior pero con desplazamiento t+1 e intervalo ampliado en la parte izquierda del plano.
# Sistema sobre señal de entrada
y = x.subs(t,t+1)
# intervalo de t[a,b] para graficar
a = -2
b = 2*np.pi
muestras = 101
Ejemplo 3. Sistema con amplitud variable en tiempo (AM)
y(t) = x(t) \cos(t+1)# entradas desplazadas en t, revisar salida # Sistemas Causales y NO causales en tiempo # Oppenheim 1.12 p47 pdf78 import numpy as np import sympy as sym import matplotlib.pyplot as plt equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, 'numpy'] # INGRESO t = sym.Symbol('t', real=True) x = sym.Symbol('x', real=True) t0 = 1.0 # señales de entrada f = sym.exp(-t)*sym.Heaviside(t) w = f.subs(t,t-t0) # sistema y = x*sym.cos(t+1) # intervalo de t[a,b] para graficar a = 0 b = 2*np.pi muestras = 101 # PROCEDIMIENTO # Sistema sobre señal de entrada yf = y.subs(x,f).doit() yw = y.subs(x,w).doit() # Para gráfica ti = np.linspace(a,b,muestras) # señales de entrada ft = sym.lambdify(t,f) wt = sym.lambdify(t,w) # señales de salida yft = sym.lambdify(t,yf,modules=equivalentes) ywt = sym.lambdify(t,yw,modules=equivalentes) # evalua entradas ti fi = ft(ti) wi = wt(ti) # evalua salidas ti yfi = yft(ti) ywi = ywt(ti) # SALIDA print('yf:') sym.pprint(yf) print('yw:') sym.pprint(yw) # grafica plt.subplot(211) # entradas plt.plot(ti,fi,'--', label='f(t)') plt.plot(ti,wi,'--',color='green', label='w(t)=f(t-t0)') plt.axhline(0) plt.axvline(0,color='red') plt.xlabel('ti') plt.ylabel('entradas') plt.title('Sistema y='+str(y)+ ' ¿Causal?') plt.legend() plt.grid() plt.subplot(212) # salidas plt.plot(ti,yfi,'--',label='yf=y[f(t)]') plt.plot(ti,ywi,'--',color='green', label='yw=y[w(t)]') plt.axhline(0) plt.axvline(0,color='red') plt.xlabel('ti') plt.ylabel('salidas') plt.legend() plt.grid() plt.show()
Ejemplo 4. desplazamiento e inversión en tiempo
# entradas desplazadas en t, revisar salida # Sistemas Causales y NO causales en tiempo # Hsu 1.5.C p17 import numpy as np import sympy as sym import matplotlib.pyplot as plt equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, 'numpy'] # INGRESO t = sym.Symbol('t', real=True) x = sym.Symbol('x', real=True) t0 = 0.75 # señales de entrada f = sym.cos(t)*sym.Heaviside(t) w = f.subs(t,t-t0) # sistema y = x + sym.Subs(x,t,(5-t),evaluate=False) # intervalo de t[a,b] para graficar a = -2*np.pi b = 2*np.pi muestras = 101 # PROCEDIMIENTO # Sistema sobre señal de entrada yf = y.subs(x,f).doit() yw = y.subs(x,w).doit() # Para gráfica ti = np.linspace(a,b,muestras) # señales de entrada ft = sym.lambdify(t,f) wt = sym.lambdify(t,w) # señales de salida yft = sym.lambdify(t,yf,modules=equivalentes) ywt = sym.lambdify(t,yw,modules=equivalentes) # evalua entradas ti fi = ft(ti) wi = wt(ti) # evalua salidas ti yfi = yft(ti) ywi = ywt(ti) # SALIDA print('yf:') sym.pprint(yf) print('yw:') sym.pprint(yw) # grafica plt.subplot(211) # entradas plt.plot(ti,fi,'--', label='f(t)') plt.plot(ti,wi,'--',color='green', label='w(t)=f(t-t0)') plt.axhline(0) plt.axvline(0,color='red') plt.xlabel('ti') plt.ylabel('entradas') plt.title('Sistema y='+str(y)+ ' ¿Causal?') plt.legend() plt.grid() plt.subplot(212) # salidas plt.plot(ti,yfi,'--',label='yf=y[f(t)]') plt.plot(ti,ywi,'--',color='green', label='yw=y[w(t)]') plt.axhline(0) plt.axvline(0,color='red') plt.xlabel('ti') plt.ylabel('salidas') plt.legend() plt.grid() plt.show()
[ concepto ] [ retraso ] [ adelanto ] [ amplitud ] [ inversión ] [ algoritmo ]