Categoría: Unidad 6 Sistemas Lineales LTI Discretos

Referencia: Lathi 3.8 p282, Oppenheim 2.1.2 p77 pdf108, Hsu 2.6.C p62

Una señal discreta de entrada x[n] se representa como una superposición de versiones escaladas de un conjunto de impulsos unitarios desplazados δ[n-k], cada uno con valor diferente de cero en un solo punto en el tiempo, especificado por el valor de k.

La respuesta de un sistema lineal y[n] a x[n] es la superposición de las respuestas escaladas del sistema a cada uno de estos impulsos desplazados.

Si usamos h_k[n] como la respuesta del sistema lineal al impulso unitario desplazado por δ[n-k]. La respuesta y[n] del sistema lineal a la entrada x[n] en la ecuación será la combinación lineal ponderada de las respuesta básicas.

$y[n] = \sum_{k=-\infty}^{+\infty} x[k]h_{k}[n]$

Si se conoce la respuesta de un sistema lineal al conjunto de impulsos unitarios desplazados, podemos construir una respuesta a una entrada arbitraria.

Si el sistema lineal también es invariante en el tiempo, entonces estas respuestas a impulsos unitarios desplazados en el tiempo son todas las versiones desplazadas en el tiempo unas de otras.

h[n] es la salida del sistema LTI cuando δ[n] es la entrada. Entonces para un sistema LTI la ecuación se vuelve.

$y[n] = \sum_{k=-\infty}^{+\infty} x[k]h[n-k]$

El resultado se conoce como la «convolución de suma» o «suma de superposición» y la operación miembro derecho de la ecuación se llama convolución de las secuencias x[n] y h[n] que se representa de manera simbólica como:

$y[n] = x[n]*h[n]$

---

Ejemplo

Referencia: Openheim Ejemplo 2.4 p85 pdf116

Considere una entrada x[n] y una respuesta al impulso unitario h[n] dada por:

x[n] = (u[n]-u[n-5])
h[n] = αⁿ (u[n]-u[n-7])

con α>1.  Para el ejercicio, α=1.5.

Nota: Para el algoritmo, si α es un entero, por ejemplo 2, usar α=2.0, para que la operación potencia se realice con números reales, como entero se puede saturar y dar error.

---

Al aplicar la suma de convolución obtiene:

Para aplicar el algoritmo se requiere definir u[n], por ser parte de las funciones x[n] y h[n]. Dado que la operación requiere valores fuera del rango muestreado para n, la sección suma convolución utiliza las funciones en lugar de los vectores xi, hi.

La función está definida en un intervalo simétrico, por lo que el rango de trabajo [a,b] se mantiene de la forma [-b,b] en las instrucciones.

# Respuesta a impulsos - forma discreta
# Ejemplo Oppenheim Ejemplo 2.3 p83/pdf111
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
# Rango [a,b], simétrico a 0
b = 15 ; a = -b

alfa = 1.5
u = lambda n: np.piecewise(n,n>=0,[1,0])

x = lambda n: u(n)-u(n-5)
h = lambda n: (alfa**n)*(u(n)-u(n-7))


# PROCEDIMIENTO
ni = np.arange(a,b+1,1)
xi = x(ni)
hi = h(ni)

# Suma de Convolucion x[n]*h[n]
muestras = len(xi)
yi = np.zeros(muestras, dtype=float)
for i in range(0,muestras):
    suma = 0
    for k in range(0,muestras):
        suma = suma + x(ni[k])*h(ni[i]-ni[k])
    yi[i] = suma

# yi = np.convolve(xi,hi,'same')

# SALIDA - GRAFICA
plt.figure(1)
plt.suptitle('Suma de Convolución x[n]*h[n]')

plt.subplot(311)
plt.stem(ni,xi, linefmt='b--',
         markerfmt='bo',basefmt='k-')
plt.ylabel('x[n]')

plt.subplot(312)
plt.stem(ni,hi, linefmt='b--',
         markerfmt='ro',basefmt='k-')
plt.ylabel('h[n]')

plt.subplot(313)
plt.stem(ni,yi, linefmt='g-.',
         markerfmt='mo', basefmt='k-')

plt.ylabel('x[n]*h[n]')
plt.xlabel('n')

plt.show()

La suma convolución se encuentra también disponible con Numpy en np.convolve(), la  sección de suma convolución se puede reemplazar y obtener los mismos resultados. Considere que para éste caso se usan los vectores xi y hi.

yi = np.convolve(xi,hi,'same')

el algoritmo se puede aplicar a otros ejercicios para comprobar los resultados.

Continúe con el ejercicio 2.5 del libro.

Referencia: Lathi Ejemplo 3.21 p286

Determine la respuesta a estado cero de un sistema LTID descrito por la ecuación de diferencias mostrada,

$y[n+2] - 0.6 y[n+1] - 0.16 y[n] = 5x[n+2]$

Si la entrada es x[n] = 4^-n u[n]

---

Para realizar el diagrama, se desplaza la ecuación en dos unidades

$y[n] - 0.6 y[n-1] - 0.16 y[n-2] = 5x[n]$ $y[n] = 0.6 y[n-1] + 0.16 y[n-2] + 5x[n]$

las condiciones iniciales es estado cero son todas cero.

---

La entrada puede expresada como:

$x[n] = 4^{-n} \mu [n] = \Big( \frac{1}{4} \Big)^n \mu [n]$ $x[n] = 0.25^{n} \mu [n]$

la respuesta al impulso del sistema se encontró en el ejemplo de la sección anterior:

$h[n] = [ (-0.2)^n +4 (0.8)^n ] \mu [n]$

Por lo que:

$y[n] = x[n] \circledast h[n]$ $= 0.25^{n} \mu [n] \circledast \Big[ (-0.2)^n +4 (0.8)^n \Big] \mu [n]$ $= 0.25^{n} \mu [n] \circledast (-0.2)^n \mu [n] + 0.25^{n} \mu [n] \circledast 4 (0.8)^n \mu [n]$

usando la tabla de convolución de sumas para tener:

$y[n] = \Bigg[ \frac{0.25^{n+1}-(-0.2)^{n+1}}{0.25-(-0.2)} + 4 \frac{0.25^{n+1} - 0.8^{n+1}}{0.25-0.8}\Bigg] \mu [n]$ $= \Bigg[2.22 \Big[ 0.25^{n+1} - (-0.2)^{n+1}\Big] +$ $- 7.27 \Big[ 0.25^{n+1} - (0.8)^{n+1}\Big]\Bigg] \mu [n]$ $= \Big[ -5.05 (0.25)^{n+1} - 2.22(-0.2)^{n+1} + 7.27 (0.8)^{n+1} \Big] \mu [n]$

recordando que ϒⁿ⁺¹ = ϒ(ϒ)ⁿ se puede expresar,

$y[n] = \Big[-1.26 (0.25)^{n} + 0.444 (-0.2)^{n} +5.81(0.8)^{n}\Big] \mu [n]$

---

Desarrollo numérico con Python

La respuesta a estado cero se encuentra en forma numérica con la expresión:

$y[n] = x[n] \circledast h[n]$

que en Numpy es np.convolve() y facilita el cálculo de la convolucion de sumas. El tema de convolución con Python se desarrolla en la siguiente sección.

La respuesta del algoritmo se presenta en la gráfica:

En el algoritmo se compara la solución numérica yi[n] con la solución analítica yia[n], obteniendo un error del orden 10^-3 dado por el truncamiento de dígitos en ambos métodos.

 error numerico vs analítico: 
 maximo de |error|:  0.006000000000000227
 errado: 
[-0.          0.         -0.          0.         -0.          0.
 -0.          0.         -0.          0.         -0.         -0.
 -0.          0.          0.         -0.006      -0.0058     -0.00509
 -0.0041445  -0.00334173 -0.00267831 -0.0021442  -0.00171569 -0.00137264
 -0.00109813 -0.00087851 -0.00070281 -0.00056225 -0.0004498  -0.00035984
 -0.00028787]

El algoritmo continúa como un anexo a los algoritmos de respuesta a entrada cero e impulso.

Instrucciones en Python

# Sistema LTID. Respuesta entrada cero, 
# Respuesta a impulso
# resultado con raices Reales
# ejercicio lathi ejemplo 3.121 p286
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

# INGRESO
# coeficientes E con grado descendente
Q = [1., -0.6, -0.16]
P = [5.,  0,    0   ]
# condiciones iniciales con n ascendente -2,-1, 0
inicial = [25/4, 0.] 

# PROCEDIMIENTO
# raices
gamma = np.roots(Q)

# revisa raices numeros complejos
revisaImag = np.iscomplex(gamma)
escomplejo = np.sum(revisaImag)
if escomplejo == 0:
    
    # coeficientes de ecuacion
    m = len(Q)-1
    A = np.zeros(shape=(m,m),dtype=float)
    for i in range(0,m,1):
        for j in range(0,m,1):
            A[i,j] = gamma[j]**(-m+i)
    ci = np.linalg.solve(A,inicial)

    # ecuacion yn
    n = sym.Symbol('n')
    y0 = 0
    for i in range(0,m,1):
        y0 = y0 + ci[i]*(gamma[i]**n)

    # Respuesta impulso
    ni = np.arange(-m,m,1)
    hi = np.zeros(m, dtype=float)
    xi = np.zeros(2*m, dtype=float)
    xi[m] = 1 # impulso en n=0

    # h[n] iterativo
    p_n = len(P)
    for i in range(0,m,1):
        for k in range(m,2*m,1):
            hi[i] = hi[i] - Q[k-m]*hi[m-k+1]
        for k in range(0,p_n,1):
            hi[i] = hi[i] + P[k]*xi[m+i]
    Bh = hi[:m]

    # coeficientes de ecuacion
    m = len(Q)-1
    Ah = np.zeros(shape=(m,m),dtype=float)
    for i in range(0,m,1):
        for j in range(0,m,1):
            Ah[i,j] = gamma[j]**(i)
    ch = np.linalg.solve(Ah,Bh)

    # ecuacion hn
    hn = 0
    for i in range(0,m,1):
        hn = hn + ch[i]*(gamma[i]**n)

    # Respuesta de estado cero ----------------
    # Rango [a,b], simetrico a 0
    b = 15 ; a = -b
    
    u = lambda n: np.piecewise(n,[n>=0,n<0],[1,0])
    
    x = lambda n: (0.25)**(n)*u(n)
    hL = sym.lambdify(n,hn,'numpy')
    h = lambda n: hL(n)*u(n)
    
    # PROCEDIMIENTO
    ni = np.arange(a,b+1,1)
    xi = x(ni)
    hi = h(ni)
    
    # Suma de Convolucion x[n]*h[n]
    yi = np.convolve(xi,hi,'same')
    
    # compara respuesta numerica con resultado analitico
    ya = lambda n: (-1.26*(0.25**n)+0.444*((-0.2)**n)+5.81*(0.8**n))*u(n)
    yia = ya(ni)

    errado = yia-yi
    erradomax = np.max(np.abs(errado))

        
# SALIDA
print('respuesta entrada cero: ')
print('raices: ', gamma)
if escomplejo == 0:
    print('Matriz: ')
    print(A)
    print('Ci:     ', ci)
    print('yn:  ')
    sym.pprint(y0)
    
    print('\n respuesta impulso: ')
    print('hi:',hi)
    print('Matriz: ')
    print(Ah)
    print('Ch: ',ch)
    print('n>=0, hn:  ')
    sym.pprint(hn)

    print('\n error numerico vs analitico: ')
    print(' maximo de abs(error): ', erradomax)
    print(' errado: ')
    print(errado)

    # SALIDA - GRAFICA
    plt.figure(1)
    plt.suptitle('Suma de Convolucion x[n]*h[n]')

    plt.subplot(311)
    plt.stem(ni,xi, linefmt='b--',
             markerfmt='bo',basefmt='k-')
    plt.ylabel('x[n]')

    plt.subplot(312)
    plt.stem(ni,hi, linefmt='b--',
             markerfmt='ro',basefmt='k-')
    plt.ylabel('h[n]')

    plt.subplot(313)
    plt.stem(ni,yi, linefmt='g-.',
             markerfmt='mo', basefmt='k-')
    plt.stem(ni,yia, linefmt='y-.',
             markerfmt='mD', basefmt='k-')

    plt.ylabel('x[n]*h[n]')
    plt.xlabel('n')

    plt.show()
    
else:
    print(' existen raices con números complejos.')
    print(' usar algoritmo de la sección correspondiente.')

Referencia: Lathi Ejemplo 3.17, 3.18  y 3.19 p277-278

Determine la respuesta al impulso unitario de un sistema LTID descrito por la ecuación de diferencias mostrada,

$y[n+2] - 0.6 y[n+1] - 0.16 y[n] = 5x[n+2]$

---

Para el diagrama se usa la ecuación desplazada en dos unidades,

$y[n] - 0.6 y[n-1] - 0.16 y[n-2] = 5x[n]$ $y[n] = 0.6 y[n-1] + 0.16 y[n-2] + 5x[n]$

En la entrada se usa un impulso unitario x[n] = δ[n]

Desarrollo Analítico

Se requieren al menos dos valores iniciales en el ejercicio, por lo que se emplea la ecuación en forma iterativa, recordando que x[n] = δ[n], siendo entonces y[n] = h[n]

$y[n] - 0.6 y[n-1] - 0.16 y[n-2] = 5x[n]$ $h[n] - 0.6 h[n-1] - 0.16 h[n-2] = 5\delta [n]$

aplicando para n=0

$h[0] - 0.6 h[-1] - 0.16 h[-2] = 5\delta[0]$ $h[0] - 0.6 (0) - 0.16 (0) = 5(1)$ $h[0] = 5$

luego se aplica para n = 1

$h[1] - 0.6 h[0] - 0.16 h[-1] = 5 \delta[1]$ $h[1] - 0.6 (5) - 0.16 (0) = 5(0)$ $h[1] = 3$

El ejercicio es continuación del primer ejercicio de respuesta a entrada cero, por lo que simplificamos el desarrollo como

$(E^2 - 0.6 E - 0.16) y[n] = 5 E^2 x[n]$ $\gamma^2 - 0.6 \gamma - 0.16 = 0$

con raíces características γ₁=-0.2 y γ₂=0.8,

con los modos característicos se tiene que

$y_c[n] = c_1 (-0.2)^n + c_2 (0.8)^n$

que se convierte a:

$h[n] = [c_1 (-0.2)^n + c_2 (0.8)^n ] \mu [n]$

Para determinar c₁ y c₂ se recurre a encontrar dos valores de forma iterativa, con n=0 y n=1.

$h[0] = [c_1 (-0.2)^0 + c_2 (0.8)^0 ] \mu [0]$ $h[0] = c_1 + c_2$ $h[1] = [c_1 (-0.2)^1 + c_2 (0.8)^1 ] \mu [1]$ $h[1] = -0.2 c_1 + 0.8 c_2$

los valores de h[0]=5 y h[1]=3 se encontraron de forma iterativa

$5 = c_1 + c_2$ $3 = -0.2 c_1 + 0.8 c_2$

resolviendo con Python:

>>> import numpy as np
>>> A = [[ 1., 1.],
         [-0.2, 0.8]]
>>> B = [5.,3.]
>>> np.linalg.solve(A,B)
array([1., 4.])
>>> 

encontrando que c₁=1 y c₂=4

teniendo como resultado final:

$h[n] = [ (-0.2)^n +4 (0.8)^n ] \mu [n]$

---

Algoritmo en Python

La respuesta para el procedimiento anterior realizada con Python es:

 respuesta impulso: 
hi: [5. 3.]
Matriz: 
[[ 1.   1. ]
 [ 0.8 -0.2]]
Ch:  [4. 1.]
n>=0, hn:  
        n          n
1.0*-0.2  + 4.0*0.8 
>>>

se desarrolla el algoritmo a partir de entrada cero, continuando con el cálculo iterativo de h[n] para los valores iniciales, luego determina los valores de los coeficientes de la ecuación h[n]

# Sistema LTID. Respuesta impulso
# QE con raices Reales NO repetidas Lathi ejemplo 3.13 pdf271
# Lathi ejemplo 3.18 y 3.19 pdf278,
# blog.espol.edu.ec/telg1001
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

# INGRESO
# coeficientes E con grado descendente
QE = [1., -0.6, -0.16]
PE = [5.,  0,    0   ]
# condiciones iniciales ascendente ...,y[-2],y[-1]
inicial = [25/4, 0.]

tolera = 1e-6  # casi_cero
muestras = 10  # para grafica

# PROCEDIMIENTO
# Respuesta a ENTRADA CERO
# raices, revisa numeros complejos
gamma = np.roots(QE)
revisaImag = np.iscomplex(gamma)
escomplejo = np.sum(revisaImag)

# coeficientes de ecuacion
m_q = len(QE)-1
Ac = np.zeros(shape=(m_q,m_q),dtype=float)

# revisa si parte compleja <tolera o casi_cero 
if escomplejo>0:
    for i in range(0,m_q,1):
        valorimag = np.imag(gamma[i])
        if np.abs(valorimag)<tolera:
            gamma[i] = float(np.real(gamma[i]))
    sumaj = np.sum(np.abs(np.imag(gamma)))
    if sumaj <tolera:
        print(sumaj)
        gamma = np.real(gamma)
        escomplejo = 0

# revisa repetidos
unicoscuenta = np.unique(gamma,return_counts=True)
repetidas = np.sum(unicoscuenta[1]-1)

# Respuesta impulso h[n]
ki = np.arange(-m_q,m_q,1)
hi = np.zeros(m_q, dtype=float)
xi = np.zeros(2*m_q, dtype=float)
xi[m_q] = 1 # impulso en n=0
Ah = np.zeros(shape=(m_q,m_q),dtype=float)

# h[n] iterativo
p_n = len(PE)
for i in range(0,m_q,1):
    for k in range(m_q,2*m_q,1):
        hi[i] = hi[i] - QE[k-m_q]*hi[m_q-k+1]
    for k in range(0,p_n,1):
        hi[i] = hi[i] + PE[k]*xi[m_q+i]
Bh = np.copy(hi[:m_q])

# coeficientes de ecuacion
for i in range(0,m_q,1):
    for j in range(0,m_q,1):
        Ah[i,j] = gamma[j]**(i)
ch = np.linalg.solve(Ah,Bh)

# ecuacion hn
n = sym.Symbol('n')
hn = 0*n
for i in range(0,m_q,1):
    hn = hn + ch[i]*(gamma[i]**n)

# SALIDA
if escomplejo == 0: 
    print('\n respuesta impulso: ')
    print('Bh:',Bh)
    print('Matriz: ')
    print(Ah)
    print('Ch: ',ch)
    print('n>=0, hn:  ')
    sym.pprint(hn)
else:
    print(' existen raices con números complejos.')
    print(' usar algoritmo de la sección correspondiente.')
    

# grafica datos
ki = np.arange(-m_q,muestras,1)
hi = np.zeros(muestras+m_q)

if escomplejo == 0: 
    # evaluación de h[n]
    h_n = sym.lambdify(n,hn)
    hi[m_q:] = h_n(ki[m_q:])

    # grafica h[n]
    plt.stem(ki,hi,label='h[n]',
             markerfmt ='C1o',
             linefmt='C2--')
    plt.legend()
    plt.grid()
    plt.ylabel('h[n]')
    plt.xlabel('ki')
    plt.title('h[n] = '+str(hn))
    plt.show()

Comentario: Aunque es relativamente simple determinar la respuesta al impulso h[n] usando el método descrito, el desarrollo del tema se realiza mejor en la unidad con Transformada z. Lathi p280.

El algoritmo integra los casos presentados en los ejercicios anteriores para:

1. raíces reales diferentes
2. raíces con números complejos
3. raíces reales repetidas

---

Instrucciones en Python

EL detalle de los pasos se encuentra en los ejercicios con Python que se han integrado por caso.

# Sistema LTID. Respuesta entrada cero
# QE con raices Reales NO repetidas Lathi ejemplo 3.13 pdf271
# QE con raices Reales Repetidas Lathi ejemplo 3.15 p274
# QE con raices Complejas Lathi ejemplo 3.16 p275
# blog.espol.edu.ec/telg1001
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

# INGRESO
# coeficientes E con grado descendente
QE = [1.0, -1.56, 0.81]
PE = [0., 1., 3.]
# condiciones iniciales ascendente ...,y[-2],y[-1]
inicial = [1.,2.]

tolera = 1e-6  # casi_cero

# PROCEDIMIENTO
# Respuesta a ENTRADA CERO
# raices, revisa numeros complejos
gamma = np.roots(QE)
revisaImag = np.iscomplex(gamma)
escomplejo = np.sum(revisaImag)

# coeficientes de ecuacion
m_q = len(QE)-1
Ac = np.zeros(shape=(m_q,m_q),dtype=float)

# revisa si parte compleja <tolera o casi_cero 
if escomplejo>0:
    for i in range(0,m_q,1):
        valorimag = np.imag(gamma[i])
        if np.abs(valorimag)<tolera:
            gamma[i] = float(np.real(gamma[i]))
    sumaj = np.sum(np.abs(np.imag(gamma)))
    if sumaj <tolera:
        print(sumaj)
        gamma = np.real(gamma)
        escomplejo = 0

# revisa repetidos
unicoscuenta = np.unique(gamma,return_counts=True)
repetidas = np.sum(unicoscuenta[1]-1)

# Determina coeficientes ci de Y[n]
# raices Reales no repetidas
if escomplejo == 0 and repetidas==0:
    for i in range(0,m_q,1):
        for j in range(0,m_q,1):
            Ac[i,j] = gamma[j]**(-m_q+i)
    ci = np.linalg.solve(Ac,inicial)
    
# raices Reales repetidas
if escomplejo == 0 and repetidas > 0:
    for i in range(0,m_q,1):
        for j in range(0,m_q,1):
            Ac[i,j] = ((-m_q+i)**j)*gamma[j]**(-m_q+i)
    ci = np.linalg.solve(Ac,inicial)

# raices Complejas
if escomplejo > 0:
    g_magnitud = np.absolute(gamma)
    g_angulo = np.angle(gamma)

    for i in range(0,m_q,1):
        k = -(m_q-i)
        a = np.cos(np.abs(g_angulo[i])*(k))*(g_magnitud[i]**(k))
        b = -np.sin(np.abs(g_angulo[i])*(k))*(g_magnitud[i]**(k))
        Ac[i] = [a,b]
    Ac = np.array(Ac)
    cj = np.linalg.solve(Ac,inicial)

    theta = np.arctan(cj[1]/cj[0])
    ci = cj[0]/np.cos(theta)

# ecuacion y0 entrada cero
n = sym.Symbol('n')
y0 = 0*n

if escomplejo == 0 and repetidas==0:
    for i in range(0,m_q,1):
        y0 = y0 + ci[i]*(gamma[i]**n)
        
if escomplejo == 0 and repetidas > 0:
    for i in range(0,m_q,1):
        y0 = y0 + ci[i]*(n**i)*(gamma[i]**n)
    y0 = y0.simplify()

if escomplejo > 0:
    y0 = ci*(g_magnitud[0]**n)*sym.cos(np.abs(g_angulo[i])*n - theta)
    
# SALIDA
print('respuesta entrada cero: ')
print('raices: ', gamma)
if escomplejo == 0:
    if repetidas>0:
        print('Raices repetidas: ', repetidas)
    print('Matriz: ')
    print(Ac)
    print('Ci:     ', ci)
    print('y0:')
    sym.pprint(y0)
if escomplejo > 0:
    print('raices complejas: ', escomplejo)
    print('magnitud:',g_magnitud)
    print('theta:',g_angulo)
    print('Matriz: ')
    print(Ac)
    print('Cj: ', cj)
    print('Ci: ',ci)
    print('y0: ')
    sym.pprint(y0)

Los siguientes ejercicios de LTI Discretos muestran los desarrollos  cuando el denominador de la función de transferencia tiene:

1. raíces reales diferentes (No repetidas)
2. raíces reales repetidas
3. raíces con números complejos

…

---

Ejercicio 1. Raíces reales diferentes

Referencia: Lathi Ejemplo 3.13 p271

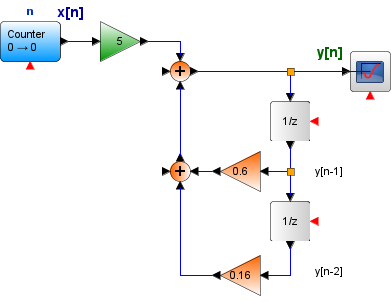
Para un sistema LTID descrito por la ecuación de diferencias mostrada,

$y[n+2] - 0.6 y[n+1] - 0.16 y[n] = 5x[n+2]$

encuentre la respuesta a entrada cero y₀[n] del sistema dadas las condiciones iniciales y[-1]=0, y[-2] =25/4, ante una entrada

$x[n]= 4^{-n} \mu [n]$

(El componente de estado cero se calcula en la sección correspondiente)

---

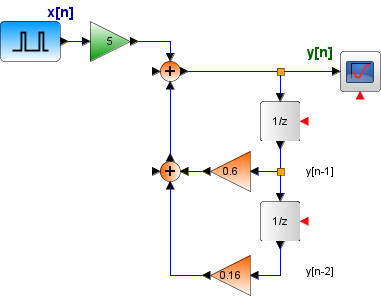
Para realizar el diagrama, se desplaza la ecuación en dos unidades

$y[n] - 0.6 y[n-1] - 0.16 y[n-2] = 5x[n]$ $y[n] = 0.6 y[n-1] + 0.16 y[n-2] + 5x[n]$

Para respuesta a entrada cero se usa x[n] = 0

1.1 Desarrollo analítico

$y[n+2] - 0.6 y[n+1] - 0.16 y[n] = 5x[n+2]$

La ecuación del sistema en notación de operador E es:

$E^2 y[n] - 0.6 E y[n] - 0.16 y[n] = 5 E^2 x[n]$ $(E^2 - 0.6 E - 0.16) y[n] = 5 E^2 x[n]$

que para entrada cero tiene x[n]=0,

$(E^2 - 0.6 E - 0.16) y[n] = 0$

tiene el polinomio característico,

$\gamma^2 - 0.6 \gamma - 0.16 = 0$ $(\gamma+0.2) (\gamma - 0.8) = 0$

con raíces características γ₁=-0.2 y γ₂=0.8, obtenidas con  instrucciones con Python:

raices:
[ 0.8 -0.2]
coeficientes:
[0.8 0.2] 

la repuesta a entrada cero tiene la forma

$y_0[n] = c_1 (-0.2)^n + c_2 (0.8)^n$

se usan las condiciones iniciales para determinar las constantes c₁ y c₂ aplicadas como:

$y_0[-1] = c_1 (-0.2)^{-1} + c_2 (0.8)^{-1}$ $0 = -5 c_1 + 1.25 c_2$ $y_0[-2] = c_1 (-0.2)^{-2} + c_2 (0.8)^{-2}$ $\frac{25}{4} = 25 c_1 + 1.5625 c_2$

se tiene el sistema de ecuaciones

$0 = -5 c_1 + 1.25 c_2$ $\frac{25}{4} = 25 c_1 + 1.5625 c_2$

resolviendo se encuentra que: c₁ = 0.2 c₂ = 0.8

con lo que la solución tiene la expresión basado en la sumatoria de c_i ϒⁿ, para n≥0

$y_0 [n] = \frac{1}{5} (-0.2)^n + \frac{4}{5} (0.8)^n$

Instrucciones en Python

import numpy as np

coeficientes = [1.,-0.6,-0.16]
raiz = np.roots(coeficientes)
print('raices:')
print(raiz)

A = np.array([[raiz[0]**(-1) , raiz[1]**(-1)],
     [raiz[0]**(-2) , raiz[1]**(-2)]])
B = np.array([0., 25/4])
ci = np.linalg.solve(A,B)
print('coeficientes:')
print(ci)

---

1.2 Desarrollo con Python

El algoritmo requiere los coeficientes de la ecuación de diferencias Q(E) y P(E) junto a las condiciones iniciales.

QE = [1., -0.6, -0.16]
PE = [5., 0., 0.]
inicial = [25/4, 0.] 

que da como resultado:

respuesta entrada cero: 
raices:  [ 0.8 -0.2]
Matriz: 
[[ 1.5625 25.    ]
 [ 1.25   -5.    ]]
Ci:      [0.8 0.2]
y0:
        n          n
0.2*-0.2  + 0.8*0.8 

Instrucciones en Python

# Sistema LTID. Respuesta entrada cero
# resultado con raices Reales
# ejercicio Lathi ejemplo 3.13 p271
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

# INGRESO
# coeficientes E con grado descendente
QE = [1., -0.6, -0.16]
PE = [5., 0., 0.]
# condiciones iniciales ascendente ...,y[-2],y[-1]
inicial = [25/4, 0.] 

# PROCEDIMIENTO
# Respuesta a ENTRADA CERO
# raices, revisa numeros complejos
gamma = np.roots(QE)
revisaImag = np.iscomplex(gamma)
escomplejo = np.sum(revisaImag)

# coeficientes de ecuacion
m_q = len(QE)-1
Ac = np.zeros(shape=(m_q,m_q),dtype=float)

if escomplejo == 0:
    for i in range(0,m_q,1):
        for j in range(0,m_q,1):
            Ac[i,j] = gamma[j]**(-m_q+i)
    ci = np.linalg.solve(Ac,inicial)

# ecuacion y0
n = sym.Symbol('n')
y0 = 0
if escomplejo == 0:
    for i in range(0,m_q,1):
        y0 = y0 + ci[i]*(gamma[i]**n)
    
# SALIDA
print('respuesta entrada cero: ')
print('raices: ', gamma)
if escomplejo == 0:
    print('Matriz: ')
    print(Ac)
    print('Ci:     ', ci)
    print('y0:')
    sym.pprint(y0)
else:
    print(' existen raices con números complejos.')
    print(' usar algoritmo de la sección correspondiente.')

Raíces: [reales No repetidas] [reales repetidas] [números complejos]

…

---

2. Raíces repetidas

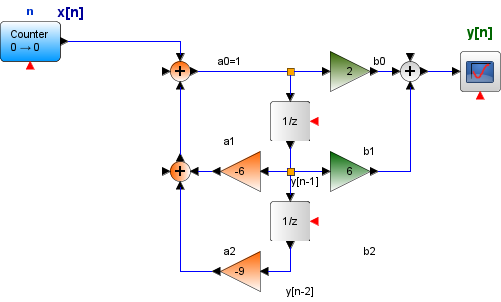
Referencia: Lathi Ejemplo 3.15 p274

$y[n+2] +6 y[n+1] + 9 y[n] = 2 x[n+2] + 6 x[n+1]$

con las condiciones iniciales y0[-1] = -1/3 y y0[-2] = -2/9

Para realizar el diagrama de bloques, se desplaza ambos lados de la ecuación en 2 unidades. Luego se despeja y[n]

$y[n] +6 y[n-1] + 9 y[n-2] = 2 x[n] + 6 x[n-1]$ $y[n] = -6 y[n-1] - 9 y[n-2] + 2 x[n] + 6 x[n-1]$

2.1 Desarrollo analítico

siguiendo los mismos pasos que en los ejercicios anteriores

$E^2 y[n] +6 E y[n] + 9 y[n] = 2 E^2 x[n] + 6 E x[n]$ $(E^2 +6 E + 9) y[n] = (2 E^2 + 6 E) x[n]$

Para entrada cero se tiene x[n] = 0

$(E^2 +6 E + 9) y[n] = (2 E^2 + 6 E) (0)$ $\gamma^2 +6 \gamma + 9 = 0$ $(\gamma + 3)( \gamma + 3) = 0$

de donde se muestra una raiz repetida γ=3, donde los modos característicos hacen que la expresión sea:

$y_0[n] = (c_1 + c_2 n) (\gamma)^n$

siguiendo el procedimiento realizado para raíces reales se puede determinar los valores de c1=4 y c2=3, con lo que se obtiene la solución:

$y_0[n] = (4 + 3n) (-3)^n$

los resultados obtenidos con el algoritmo en Python son

respuesta entrada cero: 
raices:  [-3. -3.]
Raices repetidas:  1
Matriz: 
[[ 0.11111111 -0.22222222]
 [-0.33333333  0.33333333]]
Ci:      [4. 3.]
y0:
    n              
-3.0 *(3.0*n + 4.0)
>>>

2.2 Instrucciones en Python, integrando raices reales únicas y repetidas

# Sistema LTID. Respuesta entrada cero
# QE con raices Reales NO repetidas Lathi ejemplo 3.13 pdf271
# QE con raices Reales Repetidas Lathi ejemplo 3.15 p274
# blog.espol.edu.ec/telg1001
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

# INGRESO
# coeficientes E con grado descendente
QE = [1., 6., 9.]
PE = [2., 6., 0.]
# condiciones iniciales ascendente ...,y[-2],y[-1]
 inicial = [-2/9, -1/3]

tolera = 1e-6  # casi_cero

# PROCEDIMIENTO
# Respuesta a ENTRADA CERO
# raices, revisa numeros complejos
gamma = np.roots(QE)
revisaImag = np.iscomplex(gamma)
escomplejo = np.sum(revisaImag)

# coeficientes de ecuacion
m_q = len(QE)-1
Ac = np.zeros(shape=(m_q,m_q),dtype=float)

# revisa si parte compleja <tolera o casi_cero 
if escomplejo>0:
    for i in range(0,m_q,1):
        if np.imag(gamma[i]) < tolera:
            gamma[i] = float(np.real(gamma[i]))
    sumaj = np.sum(np.imag(gamma))
    if sumaj <tolera:
        gamma = np.real(gamma)
        escomplejo = 0

# revisa repetidos
unicoscuenta = np.unique(gamma,return_counts=True)
repetidas = np.sum(unicoscuenta[1]-1)

# raices Reales no repetidas
if escomplejo == 0 and repetidas==0:
    for i in range(0,m_q,1):
        for j in range(0,m_q,1):
            Ac[i,j] = gamma[j]**(-m_q+i)
    ci = np.linalg.solve(Ac,inicial)
    
# raices Reales repetidas
if escomplejo == 0 and repetidas > 0:
    for i in range(0,m_q,1):
        for j in range(0,m_q,1):
            Ac[i,j] = ((-m_q+i)**j)*gamma[j]**(-m_q+i)
    ci = np.linalg.solve(Ac,inicial)

# ecuacion y0 entrada cero
n = sym.Symbol('n')
y0 = 0*n

if escomplejo == 0 and repetidas==0:
    for i in range(0,m_q,1):
        y0 = y0 + ci[i]*(gamma[i]**n)
        
if escomplejo == 0 and repetidas > 0:
    for i in range(0,m_q,1):
        y0 = y0 + ci[i]*(n**i)*(gamma[i]**n)
    y0 = y0.simplify()
    
# SALIDA
print('respuesta entrada cero: ')
print('raices: ', gamma)
if escomplejo == 0:
    if repetidas>0:
        print('Raices repetidas: ', repetidas)
    print('Matriz: ')
    print(Ac)
    print('Ci:     ', ci)
    print('y0:')
    sym.pprint(y0)
else:
    print(' existen raices con números complejos.')
    print(' usar algoritmo de la sección correspondiente.')

Raíces: [reales No repetidas] [reales repetidas] [números complejos]

…

---

Ejercicio 3. Raices con números complejos

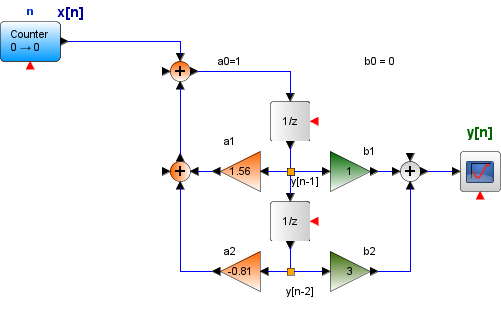
Referencia: Lathi Ejemplo 3.16 p275

Para el caso de tener raíces con números complejos se muestra el siguiente ejemplo:

$y[n+2] - 1.56 y[n+1] + 0.81 y[n] = x[n+1] + 3x[n]$

con condiciones iniciales y₀[-1]=2 y y₀[-2]=1

Para realizar el diagrama de bloques, se desplaza ambos lados de la ecuación en 2 unidades. Luego se despeja y[n]

$y[n] - 1.56 y[n-1] + 0.81 y[n-2] = x[n-1] + 3x[n-2]$ $y[n] = 1.56 y[n-1] - 0.81 y[n-2] + x[n-1] + 3x[n-2]$

3.1 Desarrollo analítico

$y[n+2] - 1.56 y[n+1] + 0.81 y[n] = x[n+1] + 3x[n]$

La expresión usando operador E:

$E^2 y[n] - 1.56 E y[n] + 0.81 y[n] = E x[n] + 3x[n]$ $(E^2 - 1.56 E + 0.81) y[n] = (E+ 3)x[n]$

para entrada cero se hace x[n] = 0

$(E^2 - 1.56 E + 0.81) y[n] = (E+ 3)(0)$

por lo que, el polinomio característico es,}

$(\gamma^2 - 1.56 \gamma + 0.81) = 0$

con raíces de números complejos

$(\gamma - (0.78 + j 0.45))(\gamma - (0.78-j 0.45)) = 0$

la raíz también se puede escribir como:

$\gamma = 0.9 e^{\pm j\frac{\pi}{6}}$

obtenida mediante:

raices:
[0.78+0.44899889j 0.78-0.44899889j]
magnitud:  [0.9 0.9]
angulo:  [ 0.52231482 -0.52231482]
>>>  

Se puede escribir la solución como:

$y_0[n] = c(0.9)n e^{j\frac{\pi}{6} } + c^{*} (0.9)n e^{-j\frac{\pi}{6}}$

Luego aplicando oas condiciones iniciales  se encuentra que

$c = 2.34 e^{-j0.17}$ $c^{*} = 2.34 e^{j0.17}$

Otra manera de desarrollo permite encontrar la solución usando la forma real de la solución, conociendo que la solución esta dada por la expresión:

$y_0[n] = c(0.9)^n \cos \Big( \frac{\pi}{6}n + \theta \Big)$

con lo que se puede crear el sistema de ecuaciones aplicando las condiciones iniciales, ademas de considerar que:

$\cos(a \pm b) = \cos(a) \cos(b) \mp \sin(a) \sin(b)$

Para y₀[-2] = 1

$1 = c(0.9)^{-2} \cos \Big( \frac{\pi}{6}(-2) + \theta \Big)$ $1 = c\frac{1}{(0.9)^2} \Big[ \cos \big(-2\frac{\pi}{6} \big) \cos ( \theta ) - \sin \big(-2\frac{\pi}{6}\big) \sin (\theta) \Big]$ $1 = c\frac{1}{0.81} \Big[ \frac{1}{2} \cos ( \theta ) - \frac{-\sqrt{3}}{2} \sin (\theta) \Big]$ $1 = c \Big[ \frac{1}{1.62} \cos ( \theta ) + \frac{\sqrt{3}}{1.62} \sin (\theta) \Big]$

Para y₀[-1] = 2

$2 = c(0.9)^{-1} \cos \Big( \frac{\pi}{6}(-1) + \theta \Big)$ $2 = c\frac{1}{0.9} \Big[ \cos \big(-\frac{\pi}{6} \big) \cos ( \theta ) - \sin \big(-\frac{\pi}{6}\big) \sin (\theta) \Big]$ $2 = c\frac{1}{0.9} \Big[ \frac{\sqrt{3}}{2} \cos ( \theta ) - \frac{-1}{2} \sin (\theta) \Big]$ $2 = c\Big[ \frac{\sqrt{3}}{1.8} \cos ( \theta ) + \frac{1}{1.8} \sin (\theta) \Big]$

con lo que se puede determinar los valores para [c cos(θ)] y [c sin(θ)]

usando una matriz A y vector B a partir de las ecuaciones

$c \cos ( \theta ) = 2.31$ $c \sin ( \theta ) = -0.4049$

al dividir  [c sin(θ)]/[c cos(θ)] = tan (θ), con lo que se obtiene el ángulo en radianes.

$\frac{ c \sin ( \theta )} {c \cos ( \theta )} = \frac{-0.4049}{2.31} = -0.17528$ $\theta = \tan ^{-1} (-0.17528) = -0.1735$

al sustituir el valor en c cos(θ) = 2.31 se tiene,

$c = \frac{2.31}{ \cos (-0.1735)} = 2.3452$

con lo que la solución se puede escribir mediante:

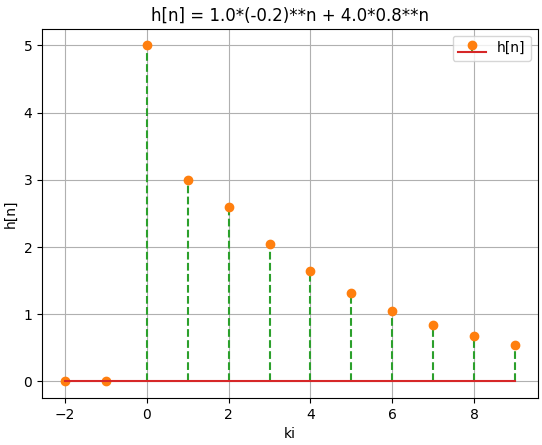
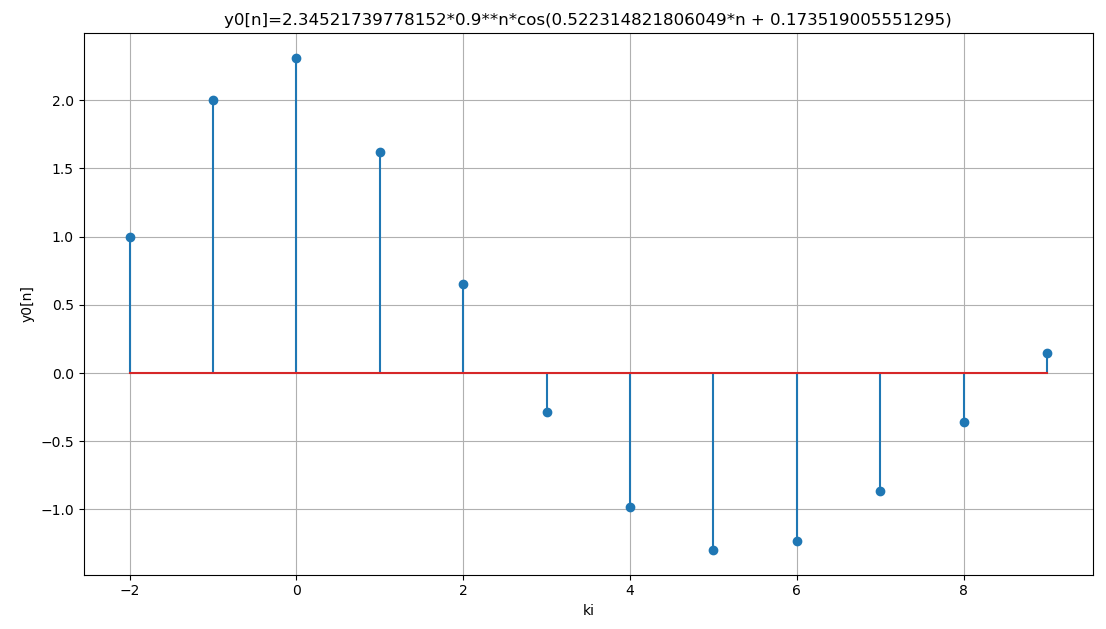
$y_0[n] = 2.3452 (0.9)^n \cos \Big( \frac{\pi}{6}n - 0.1735 \Big)$

para n≥0

Instrucciones de cálculo

import numpy as np

coeficientes = [1.,-1.56,0.81]
raiz = np.roots(coeficientes)
print('raices:')
print(raiz)

g_magnitud = np.absolute(raiz)
g_angulo = np.angle(raiz)

print('magnitud: ',g_magnitud)
print('angulo: ',g_angulo)

3.2 Algoritmo en Python, integrando raices reales y complejas

usando el algoritmo se obtienen los siguientes resultados:

Respuesta entrada cero: 
raices :  [0.78+0.44899889j 0.78-0.44899889j]
raices complejas:  2
magnitud: [0.9 0.9]
theta: [ 0.52231482 -0.52231482]
Matriz: 
[[0.62002743 1.06757851]
 [0.96296296 0.55431961]]
Cj:      [ 2.31       -0.40490078] 
Ci:  2.345217397781524
y0: 
                    n                                             
2.34521739778152*0.9 *cos(0.522314821806049*n + 0.173519005551295)
>>> 

Para el caso de raíces complejas, se añade al algoritmo anterior las instrucciones en Python:

# Sistema LTID. Respuesta entrada cero
# QE con raices Reales NO repetidas Lathi ejemplo 3.13 pdf271
# QE con raices Reales Repetidas Lathi ejemplo 3.15 p274
# QE con raices Complejas Lathi ejemplo 3.16 p275
# blog.espol.edu.ec/telg1001
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

# INGRESO
# coeficientes E con grado descendente
QE = [1.0, -1.56, 0.81]
PE = [0., 1., 3.]
# condiciones iniciales ascendente ...,y[-2],y[-1]
inicial = [1.,2.]

tolera = 1e-6  # casi_cero
muestras = 10  # para grafica

# PROCEDIMIENTO
# Respuesta a ENTRADA CERO
# raices, revisa numeros complejos
gamma = np.roots(QE)
revisaImag = np.iscomplex(gamma)
escomplejo = np.sum(revisaImag)

# coeficientes de ecuacion
m_q = len(QE)-1
Ac = np.zeros(shape=(m_q,m_q),dtype=float)

# revisa si parte compleja <tolera o casi_cero 
if escomplejo>0:
    for i in range(0,m_q,1):
        valorimag = np.imag(gamma[i])
        if np.abs(valorimag)<tolera:
            gamma[i] = float(np.real(gamma[i]))
    sumaj = np.sum(np.abs(np.imag(gamma)))
    if sumaj <tolera:
        print(sumaj)
        gamma = np.real(gamma)
        escomplejo = 0

# revisa repetidos
unicoscuenta = np.unique(gamma,return_counts=True)
repetidas = np.sum(unicoscuenta[1]-1)

# Determina coeficientes ci de Y[n]
# raices Reales no repetidas
if escomplejo == 0 and repetidas==0:
    for i in range(0,m_q,1):
        for j in range(0,m_q,1):
            Ac[i,j] = gamma[j]**(-m_q+i)
    ci = np.linalg.solve(Ac,inicial)
    
# raices Reales repetidas
if escomplejo == 0 and repetidas > 0:
    for i in range(0,m_q,1):
        for j in range(0,m_q,1):
            Ac[i,j] = ((-m_q+i)**j)*gamma[j]**(-m_q+i)
    ci = np.linalg.solve(Ac,inicial)

# raices Complejas
if escomplejo > 0:
    g_magnitud = np.absolute(gamma)
    g_angulo = np.angle(gamma)

    for i in range(0,m_q,1):
        k = -(m_q-i)
        a = np.cos(np.abs(g_angulo[i])*(k))*(g_magnitud[i]**(k))
        b = -np.sin(np.abs(g_angulo[i])*(k))*(g_magnitud[i]**(k))
        Ac[i] = [a,b]
    Ac = np.array(Ac)
    cj = np.linalg.solve(Ac,inicial)

    theta = np.arctan(cj[1]/cj[0])
    ci = cj[0]/np.cos(theta)

# ecuacion y0 entrada cero
n = sym.Symbol('n')
y0 = 0*n

if escomplejo == 0 and repetidas==0:
    for i in range(0,m_q,1):
        y0 = y0 + ci[i]*(gamma[i]**n)
        
if escomplejo == 0 and repetidas > 0:
    for i in range(0,m_q,1):
        y0 = y0 + ci[i]*(n**i)*(gamma[i]**n)
    y0 = y0.simplify()

if escomplejo > 0:
    y0 = ci*(g_magnitud[0]**n)*sym.cos(np.abs(g_angulo[i])*n - theta)
    
# SALIDA
print('respuesta entrada cero: ')
print('raices: ', gamma)
if escomplejo == 0:
    if repetidas>0:
        print('Raices repetidas: ', repetidas)
    print('Matriz: ')
    print(Ac)
    print('Ci:     ', ci)
    print('y0:')
    sym.pprint(y0)
if escomplejo > 0:
    print('raices complejas: ', escomplejo)
    print('magnitud:',g_magnitud)
    print('theta:',g_angulo)
    print('Matriz: ')
    print(Ac)
    print('Cj: ', cj)
    print('Ci: ',ci)
    print('y0: ')
    sym.pprint(y0)

# grafica datos
ki = np.arange(-m_q,muestras,1)
y0i = np.zeros(muestras+m_q)
# valores iniciales
y0i[0:m_q] = inicial[0:m_q]
# evaluación de y0[n]
y0n = sym.lambdify(n,y0)
y0i[m_q:] = y0n(ki[m_q:])

# grafica y[n] ante x[n]=0
plt.stem(ki,y0i)
plt.xlabel('ki')
plt.ylabel('y0[n]')
plt.title('y0[n]='+str(y0))
plt.grid()
plt.show()

Raíces: [reales No repetidas] [reales repetidas] [números complejos]