Categoría: Unidad 7 Sistemas LTI – Transformada z

2Eva2009TII_T2 LTI DT Dado h[n], y[n] determine x[n]

 

Referencia: Lathi Ejemplo 5.5 p510

continuando con la solución del ejercicio de condiciones iniciales,

y[n+2] – 5 y[n+1] + 6 y[n] = 3 x[n+1] + 5 x[n]

con las condiciones iniciales y[-1]=11/16, y[-2]=37/36,
ante una entrada x[n]=(-2)^-nμ[n]

Respuesta total

=

respuesta a entrada cero

+

respuesta a estado cero

En el ejemplo se encuentra que la solución total de la ecuación de diferencias se puede separar en dos componentes. El primero es generado por las condiciones iniciales y el segundo por la entrada x[n]

$\Bigg(1 - 5 \frac{1}{z} + 6 \frac{1}{z^2}\Bigg) Y[z] + \Bigg(-3 + \frac{11}{z} \Bigg) = 3\frac{1}{z-0.5}+5\frac{1}{z(z-0.5)}$ $\Bigg(1 - 5 \frac{1}{z} + 6 \frac{1}{z^2}\Bigg) Y[z] = - \Bigg(-3 + \frac{11}{z} \Bigg) + \frac{3z+5}{z(z-0.5)}$ $\Bigg(1 - 5 \frac{1}{z} + 6 \frac{1}{z^2}\Bigg) Y[z] = -\text{condiciones iniciales} + \text{entrada x[n]}$

para simplificar, se multiplica ambos lados por z²

$(z^2 - 5 z + 6 ) Y[z] = - z(-3z +11) + \frac{z(3z+5)}{(z-0.5)}$ $(z^2 - 5 z + 6 ) Y[z] = - \text{condiciones iniciales} + \text{entrada x[n]}$ $Y[z] = \frac{- z(-3z +11)}{(z^2 - 5 z + 6 )} + \frac{z(3z+5)}{(z-0.5)(z^2 - 5 z + 6 ) }$

respuesta total = (respuesta a entrada cero) + (respuesta estado cero)

continuando luego con el proceso de fracciones parciales y cambio al dominio de tiempo discreto. (realizado en desarrollo analítico), aqui se usa la transformada_z inversa con Sympy:

$y[n] = \Bigg[ \frac{26}{15}(0.5)^n - \frac{7}{3}(2)^n + \frac{18}{5}(3)^n \Bigg] \mu [n]$

---

Instrucciones en Python

Se reutilizan los algoritmos de la sección LTID Transformada z – Fracciones parciales con Python a lo que se añaden las instrucciones de los pasos anteriores.

 Hz {polos:veces} :  {3: 1, 2: 1}
 Hz {ceros:veces} :  {-5/3: 1}

 termino condiciones iniciales: 
z*(11 - 3*z)
termino entrada x[n]:  
2*z*(3*z + 5)
-------------
   2*z - 1   

 Yz = ZIR_z + ZSR_z:
  z*(11 - 3*z)        2*z*(3*z + 5)      
- ------------ + ------------------------
   2                       / 2          \
  z  - 5*z + 6   (2*z - 1)*\z  - 5*z + 6/

 Yz en fracciones parciales z:
    26*z          7*z         18*z  
------------ - --------- + ---------
15*(z - 1/2)   3*(z - 2)   5*(z - 3)

 y[n]:
/      n      n       n\             
|26*0.5    7*2    18*3 |             
|------- - ---- + -----|*Heaviside(n)
\   15      3       5  /             
>>> 

Instrucciones Python

# Transformada z - Fracciones parciales
# Y(z) = -condicion0+entradaxn = ZIR+ZSR
# Lathi Ejemplo 5.5 p510
import sympy as sym
import telg1001 as fcnm
sym.SYMPY_DEBUG=True
# INGRESO
z = sym.Symbol('z')
n = sym.Symbol('n', real=True)

# coeficientes como racional en dominio 'ZZ' enteros
a0 = sym.Rational(1/2).limit_denominator(1000)
# señal de entrada Xz
Xz = z/(z-a0)

# Hz = Pz/Qz
Pz = 3*z+5
Qz = z**2-5*z+6
Hz = Pz/Qz

# condiciones iniciales ascendente ...,y[-2],y[-1]
a1 = sym.Rational(37,36)
a2 = sym.Rational(11,6)
cond_inicio = [a1, a2]

# PROCEDIMIENTO
Fz = sym.simplify(Hz)
# polos y ceros de Fz
[P,Q] = Fz.as_numer_denom()
P = sym.poly(P,z)
Q = sym.poly(Q,z)
P_ceros = sym.roots(P)
Q_polos = sym.roots(Q)

# coeficientes QD
Q_coef  = Q.coeffs()
Q_grado = Q.degree()

# Términos de condiciones iniciales
m0 = len(cond_inicio)
term_0 = 0 
for j in range(0,Q_grado,1):
    term_grado = 0
    for i in range(m0-1-j,m0,1):
        term_cond0 = cond_inicio[i]*(z**((m0-1-j)-i ))
        term_grado = term_grado + term_cond0
    term_0 = term_0 + term_grado*Q_coef[j+1]
    
# salida y(t) a entrada x(t)
term_0  = sym.simplify(term_0*(z**2))
term_xn = sym.simplify(Pz*Xz)
ZIR_z = -sym.simplify(term_0/Q)
ZSR_z = sym.simplify(term_xn/Q)

# Y[z] = entrada0 + estado0
Yz = ZIR_z + ZSR_z

# Y[z] en fracciones parciales y parametros cuadraticos
Yzp = fcnm.apart_z(Yz)
Qs2 = fcnm.Q_cuad_z_parametros(Yzp)

# Inversa de transformada z
yn = 0*n ; Fz_revisar = []
term_sum = sym.Add.make_args(Yzp)
for term_k in term_sum:
    term_kn = fcnm.inverse_z_transform(term_k,z,n)
    if type(term_kn)==tuple:
        yn = yn + term_kn[0]
    else:
        yn = yn + term_kn
yn = yn.collect(sym.Heaviside(n))
yn = yn.collect(sym.DiracDelta(n))
yn = fcnm._round_float_is_int(yn)

# SALIDA
print(' Hz {polos:veces} : ',Q_polos)
print(' Hz {ceros:veces} : ',P_ceros)
print('\n termino condiciones iniciales: ')
sym.pprint(term_0)
print(' termino entrada x[n]:  ')
sym.pprint(term_xn)
print('\n Yz = ZIR_z + ZSR_z:')
sym.pprint(Yz)
print('\n Yz en fracciones parciales z:')
sym.pprint(Yzp)
if len(Qs2)>0:
    print('Y[z] parametros cuadraticos: ')
    for Qs2_k in Qs2:
        print(Qs2_k,':')
        for cadauno in Qs2[Qs2_k].keys():
            print(cadauno,'\t',Qs2[Qs2_k][cadauno])
print('\n y[n]:')
sym.pprint(yn)
if len(Fz_revisar)>0:
    print('\n --- revisar terminos sin transformada en tabla: ---')
    for un_term in Fz_revisar:
        print(un_term)

La transformada z convierte las ecuaciones de diferencias en expresiones algebraicas que permiten encontrar soluciones en el dominio z. A partir de las soluciones en el dominio z, se aplica la transformada inversa z que lleva a la solución en el dominio del tiempo

---

Ejercicio1

Referencia: Lathi Ejemplo 5.5 p510

Resolver

y[n+2] – 5 y[n+1] + 6 y[n]  = 3 x[n+1] + 5 x[n]

con las condiciones iniciales y[-1]=11/16, y[-2]=37/36,
ante una entrada x[n]=(2)^-nμ[n]

Desarrollo analítico

Usando la propiedad de desplazamiento de 2 unidades a la derecha.

y[n] – 5 y[n-1] +6 y[n-2]  = 3 x[n-1] + 5 x[n-2]

se aplica la transformada z, teniendo en cuenta que y[n-k] significa y[n-k]μ[n], pues consideramos solamente la situación de n≥0, y[n] esta presente incluso antes de n=0.

Teniendo así que,

$y[n] μ[n] \Leftrightarrow Y[z]$ $y[n-1] μ[n] \Leftrightarrow \frac{1}{z} Y[z] + y[-1] = \frac{1}{z} Y[z] + \frac{11}{6}$ $y[n-1] μ[n] \Leftrightarrow \frac{1}{z} Y[z] + \frac{11}{6}$ $y[n-2] μ[n] \Leftrightarrow \frac{1}{z^2} Y[z] + \frac{1}{z}y[-1] + y[-2]$ $y[n-2] \mu [n] \Leftrightarrow \frac{1}{z^2} Y[z] + \frac{1}{z}\frac{11}{6} +\frac{37}{36}$

Conociendo que para una entrada causal x[n]

x[-1] = x[-2] = … = x[-n] = 0

se tiene que:

$x[n] = (2)^{-n} \mu [n] = (2^{-1})^n \mu [n] = (0.5)^n \mu [n] \Leftrightarrow \frac{z}{z-0.5}$ $x[n-1] \mu [n] \Leftrightarrow \frac{1}{z}X[z] +x[-1] = \frac{1}{z}\frac{z}{z-0.5} +0= \frac{1}{z-0.5}$ $x[n-2] \mu [n] \Leftrightarrow \frac{1}{z^2}X[z] + \frac{1}{z}x[-1] + x[-2] =$ $= \frac{1}{z^2} \frac{z}{z-0.5} + (0) + (0) = \frac{1}{z(z-0.5)}$

en general, para una entrada causal:

$x[n-r] \mu [n] \Leftrightarrow \frac{1}{z^r}X[z]$

tomando los resultados anteriores y reemplazado en la ecuacion inicial, de tiene

$Y[z] - 5 \Bigg[ \frac{1}{z} Y[z] + \frac{11}{6}\Bigg] + 6 \Bigg[\frac{1}{z^2} Y[z] + \frac{1}{z}\frac{11}{6} +\frac{37}{36} \Bigg] =$ $= 3\frac{1}{z-0.5}+5\frac{1}{z(z-0.5)}$

reagrupando términos Y[z] y reordenando,

$\Bigg(1 - 5 \frac{1}{z} + 6 \frac{1}{z^2}\Bigg) Y[z] +\Bigg(-5\frac{11}{6}+ \frac{1}{z}\frac{11}{6}6 +6\frac{37}{36} \Bigg) =$ $= 3\frac{1}{z-0.5}+5\frac{1}{z(z-0.5)}$ $\Bigg(1 - 5 \frac{1}{z} + 6 \frac{1}{z^2}\Bigg) Y[z] + \Bigg(-3 + \frac{11}{z} \Bigg) = 3\frac{1}{z-0.5}+5\frac{1}{z(z-0.5)}$ $\Bigg(1 - 5 \frac{1}{z} + 6 \frac{1}{z^2}\Bigg) Y[z] = -\Bigg(-3 + \frac{11}{z} \Bigg) + 3\frac{1}{z-0.5}+5\frac{1}{z(z-0.5)}$

En el lado derecho se muestran términos generados por una respuesta natural y una respuesta forzada. Dicho de otra forma, se muestran términos generados por las condiciones iniciales y por la señal x[n].

reagrupando el lado derecho en forma de numerador y denominador

$\Bigg(1 - 5 \frac{1}{z} + 6 \frac{1}{z^2}\Bigg) Y[z] = \frac{3z^2 -9.5z +10.5}{z(z-0.5)}$

se puede reescribir, multiplicando cada lado por z²

$z^2\Bigg(1 - 5 \frac{1}{z} + 6 \frac{1}{z^2}\Bigg) Y[z] = z^2 \Bigg[\frac{3z^2 -9.5z +10.5}{z(z-0.5)} \Bigg]$ $(z^2 - 5 z + 6) Y[z] = \frac{z(3z^2 -9.5z +10.5)}{(z-0.5)}$ $Y[z] = \frac{z(3z^2 -9.5z +10.5)}{(z-0.5)(z^2 - 5 z + 6)}$

se aplica fracciones parciales, usando el algoritmo de la sección Transformada z-fracciones parciales

$Y[z] = \frac{26}{15}\frac{z}{z-0.5} - \frac{7}{3}\frac{z}{z-2} + \frac{18}{5}\frac{z}{z-3}$

usando la tabla de transformadas z, se obtiene como respuesta en el tiempo discreto

$y[n] = \Bigg[ \frac{26}{15}(0.5)^n - \frac{7}{3}(2)^n + \frac{18}{5}(3)^n \Bigg] \mu [n]$

Referencia: Lathi 5.1-1 p495, Oppenheim 10.3 p757, Hsu 4.5.D p174

Muchas de las transformadas X(z) de interés en la práctica son funciones racionales, que pueden ser expresadas como la suma de fracciones parciales, cuyas transformadas inversas pueden ser encontradas rápidamente en la tabla de transformadas.

Se busca evitar realizar el integral en el plano complejo requerido para encontrar la transformada inversa de z.

El método de las fracciones parciales es práctico porque cada x[n] transformable se define para n≥0, existe  su correspondiente X[z] definida para |z|>r₀ y viceversa. (r₀ es constante)

Para desarrollar y probar el algoritmo con Sympy-Python, se usará el desarrollo de los tres ejercicios siguientes, con polos únicos, repetidos y complejos. El algoritmo final del literal c integra las soluciones anteriores.

---

Ejercicio 1. Polos diferentes

Referencia: Lathi Ejercicio 5.3a p495. Hsu. ejercicio 4.29 p198

Realice la expansión en fracciones parciales de,

$X[z] = \frac{8z-19}{(z-2)(z-3)}$

Se puede encontrar que,

$X[z] = \frac{3}{(z-2)}+\frac{5}{(z-3)}$

de la tabla de transformadas z se tiene,

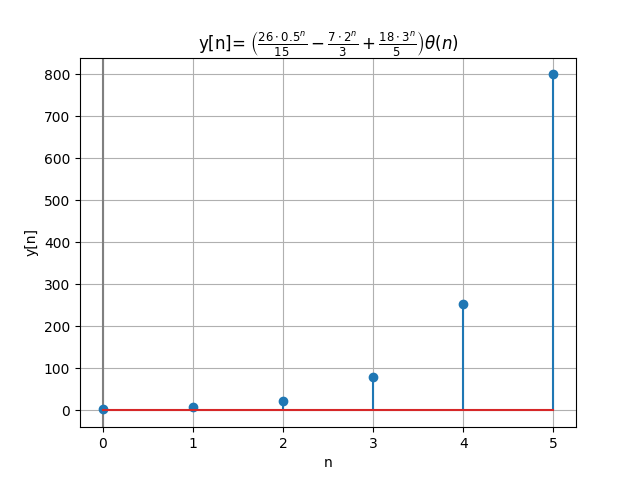
$x[n] = [3(2)^{n-1} +5(3)^{n-1}] \mu [n-1]$

Que tiene una entrada  con términos multiplicadas por μ[n-1], que es un inconveniente y no deseable. Se prefieren las transformadas respecto a μ[n].

Observando la tabla de transformadas z entre los ítems 6a y 7, se tiene que si la señal X[n] es multiplicada por u[n], el numerador tiene un factor z. Esto se consigue expandiendo en fracciones parciales X[z]/z  que son fracciones parciales modificadas cuando se tiene un factor z en el numerador y luego se restauran multiplicando el todo el resultado por z.

$\frac{X[z]}{z} = \frac{8z-19}{z(z-2)(z-3)}$ $=\frac{-19/6}{z} + \frac{3/2}{z-2} + \frac{5/3}{z-3}$

que al multiplicar ambos lados por z, se obtiene,

$X[z] =\frac{-19}{6} + \frac{3}{2}\frac{z}{z-2} + \frac{5}{3}\frac{z}{z-3}$

y usando la tabla de transformadas z se obtiene:

$x[n] = \frac{-19}{6} \delta [n] + \Big[ \frac{3}{2}(2)^n + \frac{5}{3}(3)^n \Big] \mu[n]$

que es el resultado esperado y con respuesta equivalente al resolver con algoritmo iterativo para n=0,1,2,3,…

Por este motivo, es recomendable siempre expandir en fracciones parciales X[z]/z en lugar de solo X[z], pues tiene un factor z en el numerador.

Algoritmo en Python

Para realizar el ejercicio, debemos considerar usar Sympy. Las operaciones se realizan al dividir X[x]/z y simplificar la nueva expresión Xzz, luego una expansión Xzp. El resultado se multiplica término a término por z y de añaden a la expresión total Xzfp.

El bloque de ingreso que se modifica para cada caso es:

Pz = 8*z-19
Qz = (z-2)*(z-3)

El resultado obtenido es:

 Xz:
    8*z - 19   
---------------
(z - 3)*(z - 2)

 Xz/z:
    8*z - 19    
----------------
  / 2          \
z*\z  - 5*z + 6/

 Xz/z.apart:
    3           5        19
--------- + --------- - ---
2*(z - 2)   3*(z - 3)   6*z

 Xz = (Xz/z)*z
   3*z         5*z      19
--------- + --------- - --
2*(z - 2)   3*(z - 3)   6 

>>> 

Instrucciones en Python

# Transformada z- Fracciones parciales
# Polos únicos, repetidos y complejos
# Lathi Ejercicio 5.3a pdf495
# blog.espol.edu.ec/telg1001
import sympy as sym

# INGRESO
z = sym.Symbol('z')

Pz = 8*z-19
Qz = (z-2)*(z-3)
Xz = Pz/Qz

# PROCEDIMIENTO
Fz = sym.simplify(Xz)
# fracciones parciales modificadas
Fzz = (Fz)/z
Fzm = Fzz.apart()
# fracciones parciales restaurada
terminos = Fzm.args
Fzp = 0*z
for untermino in terminos:
    Fzp = Fzp + untermino*z

# SALIDA
print('\n Xz:')
sym.pprint(Xz)
print('\n Xz/z:')
sym.pprint(Fzz)
print('\n Xz/z.apart:')
sym.pprint(Fzm)
print('\n Xz = (Xz/z)*z')
sym.pprint(Fzp)

---

Ejercicio 2. Polos repetidos

Referencia: Lathi Ejercicio 5.3b p495

Realice la expansión en fracciones parciales de,

$X[z] = \frac{z(2z^2-11z+12)}{(z-1)(z-2)^{3}}$

Antes de realizar la expansión en fracciones parciales, se divide ambos lados de la expresión para z. Es decir se usa fracciones parciales modificadas

$\frac{X[z]}{z} = \frac{1}{z}\frac{z(2z^2-11z+12)}{(z-1)(z-2)^{3}}$ $\frac{X[z]}{z} = \frac{(2z^2-11z+12)}{(z-1)(z-2)^{3}}$

donde el modelo de las fracciones parciales a aplicar es:

$\frac{(2z^2-11z+12)}{(z-1)(z-2)^{3}} = \frac{k}{z-1} + \frac{a_0}{(z-2)^3} + \frac{a_1}{(z-2)^2} + \frac{a_2}{(z-2)}$

Para encontrar las constantes, se evalúa la expresión de la izquierda con los valores de cada raíz del denominador, en cada caso se obvia el término de la raíz en el denominador,

$k = \frac{(2z^2-11z+12)}{\cancel{z-1}(z-2)^{3}} \Bigg|_{z=1} = \frac{(2(1)^2-11(1)+12)}{((1)-2)^{3}} = -3$ $a_0 = \frac{(2z^2-11z+12)}{(z-1)\cancel{(z-2)^{3}}}\Bigg|_{z=2} = \frac{(2(2)^2-11(2)+12)}{((2)-1)} = -2$

con lo que la expresión modelo se convierte en:

$\frac{(2z^2-11z+12)}{(z-1)(z-2)^{3}} = \frac{-3}{z-1} + \frac{-2}{(z-2)^3} + \frac{a_1}{(z-2)^2} + \frac{a_2}{(z-2)}$

Una forma de resolver es por ejemplo para a₂, multiplicar ambos lados por z y hacer que z→∞

$\frac{(2z^2-11z+12)}{(z-1)(z-2)^{3}} z = z \Big[\frac{-3}{z-1} + \frac{-2}{(z-2)^3} + \frac{a_1}{(z-2)^2} + \frac{a_2}{(z-2)}\Big]$ $\frac{(2z^2-11z+12)}{(z-1)(z-2)^{3}} z = \frac{-3z}{z-1} + \frac{-2z}{(z-2)^3} + \frac{a_1z}{(z-2)^2} + \frac{a_2z}{(z-2)}\Big]$ $0 = \frac{-3}{1-1/z} + \frac{-2z}{(z-2)^3} + \frac{a_1z}{(z-2)^2} + \frac{a_2}{(1-2/z)}\Big]$ $0 = -3 + (0) + (0) + a_2$ $a_2 =3$

quedando solamente una incógnita a₁ por resolver,

$\frac{(2z^2-11z+12)}{(z-1)(z-2)^{3}} = \frac{-3}{z-1} + \frac{-2}{(z-2)^3} + \frac{a_1}{(z-2)^2} + \frac{3}{(z-2)}$

El valor de a₁ se puede determinar haciendo z tomar un valor conveniente, es decir z=0 en ambos lados de la ecuación

$\frac{(2(0)^2-11(0)+12)}{((0)-1)((0)-2)^{3}} = \frac{-3}{(0)-1} + \frac{-2}{((0)-2)^3} + \frac{a_1}{((0)-2)^2} + \frac{3}{((0)-2)}$ $\frac{12}{(-1)(-8)} = \frac{-3}{-1} + \frac{-2}{-8} + \frac{a_1}{4} + \frac{-3}{-2}$ $\frac{3}{2} = 3 + \frac{1}{4} + \frac{a_1}{4} - \frac{3}{2}$ $\frac{6}{2} - \frac{13}{4}= \frac{a_1}{4}$ $-\frac{1}{4}= \frac{a_1}{4}$ $a_1 = -1$

completando la expresión:

$\frac{X[z]}{z} = \frac{-3}{z-1} + \frac{-2}{(z-2)^3} + \frac{-1}{(z-2)^2} + \frac{3}{(z-2)}$

teniendo finalmente X[z] al multiplicar ambos lados por z,

$X[z] = \frac{-3z}{z-1} + \frac{-2z}{(z-2)^3} + \frac{-1z}{(z-2)^2} + \frac{3z}{(z-2)}$

y usando la tabla de transformadas z se obtiene:

$x[n] = \Big[-3 -2 \frac{n(n-1)}{8}(2)^n - \frac{n}{2}(2)^n + 3(2)^n \Big] \mu [n]$

simplificando un poco:

$x[n] = \Big[-3 -\Big(\frac{n(n-1)}{4} + \frac{n}{2} - 3\Big)(2)^n \Big] \mu [n]$ $x[n] = -\Big[3 +\frac{1}{4}(n^2 + n-12)(2)^n \Big] \mu [n]$

Usando el algoritmo en Python anterior, el bloque de ingreso cambia a:

Pz = z*(2*z**2-11*z+12)
Qz = (z-1)*(z-2)**3

con el resultado:

 Xz:
  /   2            \
z*\2*z  - 11*z + 12/
--------------------
         3          
  (z - 2) *(z - 1)  

 Xz/z:
   2            
2*z  - 11*z + 12
----------------
       3        
(z - 2) *(z - 1)

 Xz/z.apart:
    3       3        1          2    
- ----- + ----- - -------- - --------
  z - 1   z - 2          2          3
                  (z - 2)    (z - 2) 

 Xz = (Xz/z)*z
   3*z     3*z       z         2*z   
- ----- + ----- - -------- - --------
  z - 1   z - 2          2          3
                  (z - 2)    (z - 2) 
>>> 

comparando con el resultado analítico es el mismo.

---

Ejercicio 3. Polos complejos

Referencia: Lathi Ejercicio 5.3c p495

Realice la expansión en fracciones parciales de,

$X[z] = \frac{2 z(3z+17)}{(z-1)(z^2 - 6z+25)}$

Se realiza la separación en fracciones parciales modificadas

$\frac{X[z]}{z} = \frac{2(3z+17)}{(z-1)(z^2 - 6z+25)}$

usando el método «cubrir» de Heaviside se tiene que :

$k = \frac{2(3z+17)}{\cancel{(z-1)}(z^2 - 6z+25)} \Big|_{z=1}=2$

queda por resolver la segunda parte de la fracción.

$\frac{X[z]}{z} = \frac{2}{(z-1)}+\frac{Az+B}{z^2 - 6z+25}$

Usando el método de los factores cuadráticos, se multiplica ambos lados por z y z→∞

$\frac{X[z]}{z}z= z\frac{2}{(z-1)}+z\frac{Az+B}{z^2 - 6z+25}$ $0 = \frac{2}{(1-1/z)}+\frac{Az^2+Bz}{(z^2 - 6z+25)}$ $0 = \frac{2}{(1-1/z)}+\frac{A+B\frac{1}{z}}{\frac{1}{z^2}(z^2 - 6z+25)}$ $0 = \frac{2}{(1-1/z)}+\frac{A+B\frac{1}{z}}{1 - 6\frac{1}{z}+25\frac{1}{z^2}}$ $0 = 2+A$

con lo que A = -2 , para encontrar B se usa un valor conveniente de z=0

$\frac{2 z(3z+17)}{(z-1)(z^2 - 6z+25)} = \frac{2}{(z-1)}+\frac{Az+B}{z^2 - 6z+25}$ $\frac{2 (0+17)}{(0-1)(0^2 - 6(0)+25)} = \frac{2}{((0)-1)}+\frac{-2(0)+B}{(0^2 - 6(0)+25)}$ $\frac{34}{-25} = +\frac{2}{-1}+\frac{B}{25}$ $-\frac{34}{25} + 2=\frac{B}{25}$ $-34+ 2(25) = B$

con lo que B=16

$\frac{X[z]}{z}= \frac{2}{(z-1)}+\frac{-2z+16}{z^2 - 6z+25}$ $X[z]= \frac{2}{(z-1)}+\frac{z(-2z+16)}{z^2 - 6z+25}$

con lo que es posible usar la tabla de transformadas z usando los ítems 2a y 12c. Para 12c los valores de A = -2, B = 16, |γ| =5 y a=-3.

$r = \sqrt{\frac{(-2)^2 (5)^2+(16)^2-2(-2)(-3)(16)}{(5^2 -(-3)^2}}$ $= \sqrt{\frac{100+256-192}{25-9}} =3.2$

$\beta = \cos^{-1} \Big(\frac{-(-3)}{5} \Big) = 0.927$ $\theta = \tan^{-1} \Bigg(\frac{(-2)(-3)-16}{(-2)\sqrt{(5^2 -(-3)^2}}\Bigg) = \tan^{-1}\Big( \frac{-10}{-8}\Big) = -2.246$

reemplazando en la transformada, se encuentra x[n].

$x[n] = [2+3.2(5)^n \cos(0.927n-2.246)] \mu [n]$

pasamos a probar el algoritmo, donde se encuentra que para el denominador hay raíces complejas. Otra forma de observar es que las funciones parciales aún entregan resultados con términos que tienen el denominador con grado 2. Donde hay que usar expresiones de la tabla de transformadas.

 Xz:
     2*z*(3*z + 17)    
-----------------------
        / 2           \
(z - 1)*\z  - 6*z + 25/

 Xz en fracciones parciales
   2*z*(z - 8)     2*z 
- ------------- + -----
   2              z - 1
  z  - 6*z + 25        
parametros cuadraticos: 
-2*z*(z - 8)/(z**2 - 6*z + 25) :
r 	 3.2015621187164243
gamma 	 5.0
beta 	 0.9272952180016123
theta 	 0.8960553845713439
>>>  

Instrucciones en Python

El algoritmo inicia de la misma forma que en la sección anterior. Ahora hay que revisar el grado del denominador en cada término. Si es de grado 2, se calculan los valores de r, β y θ para armar las transformada a partir de la tabla.

# Transformada z- Fracciones parciales
# Polos únicos, repetidos y complejos
# Lathi Ejercicio 5.3a pdf495
# blog.espol.edu.ec/telg1001
import numpy as np
import sympy as sym

# INGRESO
z = sym.Symbol('z')

Pz = 2*z*(3*z+17)
Qz = (z-1)*(z**2-6*z+25)

#Pz = z*(2*z**2-11*z+12)
#Qz = (z-1)*(z-2)**3

##Pz = 8*z-19
##Qz = (z-2)*(z-3)
Xz = Pz/Qz

# PROCEDIMIENTO
def apart_z(Fz):
    ''' fracciones parciales en dominio z
        modifica con factor 1/z
    '''
    Fz = sym.simplify(Fz)
    # fracciones parciales modificadas con 1/z
    Fzz = (Fz)/z
    Fzm = sym.apart(Fzz,z)
    # restaura z
    term_suma = sym.Add.make_args(Fzm)
    Fzp = 0*z
    for term_k in term_suma:
        Fzp = Fzp + term_k*z
    return(Fzp)

def Q_cuad_z_parametros(Fz):
    ''' parametros cuadraticos en dominio z
    '''

    def Q_cuad_z_term(untermino):
        ''' parametros cuadraticos en dominio z
            de un termino de fraccin parcial
        '''
        unparametro ={}
        # revisa denominador cuadratico
        [numerador,denominador] = (untermino).as_numer_denom()
        gradoD = 0
        coeficientesD = denominador
        gradoN = 0
        coeficientesN = numerador
        if not(denominador.is_constant()):
            denominador = denominador.as_poly()
            gradoD = denominador.degree()
            coeficientesD = denominador.coeffs()
        if not(numerador.is_constant()):
            numerador = numerador.as_poly()
            gradoN = numerador.degree()
            coeficientesN = numerador.coeffs()
        if gradoD == 2 and gradoN==2:
            a = float(coeficientesD[1])/2
            gamma2 = float(coeficientesD[2])
            gamma = np.sqrt(gamma2)
            A = float(coeficientesN[0])
            B = float(coeficientesN[1])
            rN = (A**2)*gamma2 + B**2 - 2*A*a*B
            rD = gamma2 - a**2
            r = np.sqrt(rN/rD)
            beta = np.arccos(-a/gamma)
            thetaN = A*a-B
            thetaD = A*np.sqrt(gamma2-a**2)
            theta = np.arctan(thetaN/thetaD)
            unparametro = {'r':r,
                           'gamma':gamma,
                           'beta':beta,
                           'theta':theta}
        return(unparametro)

    Fz = apart_z(Fz)
    # parametros denominador cuadratico
    Qs2 = {}
    term_suma = sym.Add.make_args(Fz)
    for term_k in term_suma:
        Qs2_k = Q_cuad_z_term(term_k)
        if len(Qs2_k)>0:
            Qs2[term_k] = Qs2_k
    return(Qs2)

Fz  = apart_z(Xz)
Qs2 = Q_cuad_z_parametros(Fz)

# SALIDA
print('\n Xz:')
sym.pprint(Xz)
print('\n Xz en fracciones parciales')
sym.pprint(Fz)
if len(Qs2)>0:
    print('parametros cuadraticos: ')
    for Qs2_k in Qs2:
        print(Qs2_k,':')
        for cadauno in Qs2[Qs2_k].keys():
            print(cadauno,'\t',Qs2[Qs2_k][cadauno])

La Transformada z  inversa, usa la Tabla de Pares f[n] y F[z] y los algoritmos para buscar una expresión semejante F.match() en conjunto con la tabla de propiedades y los algoritmos desarrollados en la sección anterior. El resultado se integra desde telg1001.py y se muestra en los siguientes ejemplos:

Ejemplo 1.  Transformada z inversa de una fracción X[1/z]

Referencia: Oppenheim Ejemplo 10.13 p761, Lathi Ejemplo 5.1 p490

Continuando con el ejercicio presentado para convertir x[n] a X[z], se tiene que:

$X[z] = \frac{1}{1-a z^{-1}}\text{ , } |z|>|a|$ $X[z] = \frac{z}{z-a}\text{ , } \Big|z|>|a|$

siendo la expresión de ingreso al algoritmo:

F = z/(z - 2)

el resultado es:

f[n] : (2**n*Heaviside(n), Abs(z) > 2, True)
>>> 

Ejemplo 1a. Instrucciones Python

# transformada z propiedades con Sympy
# aplicar luego de buscar en tabla de pares
import sympy as sym
import telg1001 as fcnm

# INGRESO
n = sym.Symbol('n', real=True)
z = sym.Symbol('z')
u = sym.Heaviside(n)

# (a**n)*f[n] <--> F(z/a)
F = z/(z - 2)  #f = (2**n)*u

# PROCEDIMIENTO
fn = fcnm.inverse_z_transform(F,z,n)

# SALIDA
print('f[n] :',fn)

El algoritmo presentado puede ser tomado como punto de partida para los siguientes ejercicios. Realizado para explicación conceptual.

Ejemplo 2. Transformada z inversa usando expansión en fracciones parciales

Referencia: Lathi 5.3 a

Encuentre la transformada z inversa para:

$F[z] = \frac{8z-19}{(z-2)(z-3)}$

el ingreso para el algoritmo del ejercicio anterior es:

F = (8*z-19)/((z-2)*(z-3))

con el resultado siguiente:

f[n] : (9*2**n + 10*3**n)*Heaviside(n)/6 - 19*DiracDelta(n)/6

activando la variable sym.SYMPY_DEBUG=True, se observa el proceso de fracción parcial modificada, la búsqueda en la tabla, y aplicación de una propiedad de la transformada z.

inverse_z_transform(F,z,n): (8*z - 19)/((z - 3)*(z - 2))

apart_z(F) : (8*z - 19)/((z - 3)*(z - 2))
_simplify_z: (8*z - 19)/((z - 3)*(z - 2))
  P_leadcoef: 8  ; P_zc: 1  ; P: z - 19/8
  _simplify_z k_sign: 1  ; k: 8  ; P_zc: 1  ; Q_zc: 1
    F[z]: (z - 19/8)/((z - 3)*(z - 2))
_simplify_z: (z - 19/8)/(z*(z - 3)*(z - 2))
  P_leadcoef: 8  ; P_zc: 1  ; P: z - 19/8
  Q_leadcoef: 8  ; Q_zc: z  ; Q: (z - 3)*(z - 2)
  _simplify_z k_sign: 1  ; k: 1  ; P_zc: 1  ; Q_zc: z
    F[z]: (z - 19/8)/((z - 3)*(z - 2))
  P: (8*z - 19)/8 
  Q: (z - 3)*(z - 2) 
  P_degree: 1  ; P_zeros: {19/8: 1} 
  Q_degree: 3  ; Q_poles: {3: 1, 2: 1, 0: 1}
  apart(F/z): 3/(16*(z - 2)) + 5/(24*(z - 3)) - 19/(48*z)
  ma_Qk: {a_: 48, b_: 0, c_: 1}  ; ma_Qk2: {b_: 48, a_: 0, c_: 0}
_simplify_z: -19/(48*z)
  P_leadcoef: -19  ; P_zc: 1  ; P: 1
  Q_leadcoef: 48  ; Q_zc: z  ; Q: 1
  _simplify_z k_sign: -1  ; k: 19/48  ; P_zc: 1  ; Q_zc: z
    F[z]: 1
  ma_Qk: {a_: 16, b_: -32, c_: 1}  ; ma_Qk2: {b_: 16, c_: -32, a_: 0}
_simplify_z: 3/(16*(z - 2))
  P_leadcoef: 3  ; P_zc: 1  ; P: 1
  Q_leadcoef: 16  ; Q_zc: 1  ; Q: z - 2
  _simplify_z k_sign: 1  ; k: 3/16  ; P_zc: 1  ; Q_zc: 1
    F[z]: 1/(z - 2)
  ma_Qk: {a_: 24, b_: -72, c_: 1}  ; ma_Qk2: {b_: 24, c_: -72, a_: 0}
_simplify_z: 5/(24*(z - 3))
  P_leadcoef: 5  ; P_zc: 1  ; P: 1
  Q_leadcoef: 24  ; Q_zc: 1  ; Q: z - 3
  _simplify_z k_sign: 1  ; k: 5/24  ; P_zc: 1  ; Q_zc: 1
    F[z]: 1/(z - 3)

 apart z*(Fz/z)  : 3*z/(2*(z - 2)) + 5*z/(3*(z - 3)) - 19/6 

 apart_z(F) as partial fractions: (-19/6, 3*z/(2*(z - 2)), 5*z/(3*(z - 3)))
  term_k[z]: -19/6
[0] _z_pairs_prop_inverse ----
_simplify_z: -19/6
  P_leadcoef: -19  ; P_zc: 1  ; P: 1
  Q_leadcoef: 6  ; Q_zc: 1  ; Q: 1
  _simplify_z k_sign: -1  ; k: 19/6  ; P_zc: 1  ; Q_zc: 1
    F[z]: 1
 _z_pairs_table match: 
  F: 1
  z_pair F[z]: 1  ; ma_z: {}
  z_pair f[n]: DiracDelta(n)
  try,check  : True -> True
[0]   pair f[n]: (-19*DiracDelta(n)/6, True, True)
  term_k[n]: (-19*DiracDelta(n)/6, True, True)
  term_k[z]: 3*z/(2*(z - 2))
[0] _z_pairs_prop_inverse ----
_simplify_z: 3*z/(2*(z - 2))
  P_leadcoef: 3  ; P_zc: 1  ; P: z
  Q_leadcoef: 2  ; Q_zc: 1  ; Q: z - 2
  _simplify_z k_sign: 1  ; k: 3/2  ; P_zc: 1  ; Q_zc: 1
    F[z]: z/(z - 2)

[1] z_properties_inverse_z_transform
  P: z 
  Q: z - 2 
  P_degree: 1  ; P_zeros: {0: 1} 
  Q_degree: 1  ; Q_poles: {2: 1}
  ma_P1 (a*z+ b):    {a_: 1, b_: 0}
  ma_Q1 (a*z-b)**c : {a_: 1, b_: 2, c_: 1}

 _z_property multiply (a**n)*f[n] <--> F(z/a) 
 k_sign: 1 ; k: 3/2  ; k_b: 2
 F[z]: z/(z - 1)
[2] _z_pairs_prop_inverse ----
_simplify_z: z/(z - 1)
    F[z]: z/(z - 1)
 _z_pairs_table match: 
  F: z/(z - 1)
  z_pair F[z]: z/(z - 1)  ; ma_z: {}
  z_pair f[n]: Heaviside(n)
  try,check  : True -> True
[2]   pair f[n]: (Heaviside(n), Abs(z) > 1, True)

  _z_property multiply (a**n)*f[n]:
  (3*2**n*Heaviside(n)/2, Abs(z) > 2, True)
[1]  _z_properties_inverse f[n]: (3*2**n*Heaviside(n)/2, Abs(z) > 2, True)
[0]   prop f[n]: (3*2**n*Heaviside(n)/2, Abs(z) > 2, True)
  term_k[n]: (3*2**n*Heaviside(n)/2, Abs(z) > 2, True)
  term_k[z]: 5*z/(3*(z - 3))
[0] _z_pairs_prop_inverse ----
_simplify_z: 5*z/(3*(z - 3))
  P_leadcoef: 5  ; P_zc: 1  ; P: z
  Q_leadcoef: 3  ; Q_zc: 1  ; Q: z - 3
  _simplify_z k_sign: 1  ; k: 5/3  ; P_zc: 1  ; Q_zc: 1
    F[z]: z/(z - 3)

[1] z_properties_inverse_z_transform
  P: z 
  Q: z - 3 
  P_degree: 1  ; P_zeros: {0: 1} 
  Q_degree: 1  ; Q_poles: {3: 1}
  ma_P1 (a*z+ b):    {a_: 1, b_: 0}
  ma_Q1 (a*z-b)**c : {a_: 1, b_: 3, c_: 1}

 _z_property multiply (a**n)*f[n] <--> F(z/a) 
 k_sign: 1 ; k: 5/3  ; k_b: 3
 F[z]: z/(z - 1)
[2] _z_pairs_prop_inverse ----
_simplify_z: z/(z - 1)
    F[z]: z/(z - 1)
 _z_pairs_table match: 
  F: z/(z - 1)
  z_pair F[z]: z/(z - 1)  ; ma_z: {}
  z_pair f[n]: Heaviside(n)
  try,check  : True -> True
[2]   pair f[n]: (Heaviside(n), Abs(z) > 1, True)

  _z_property multiply (a**n)*f[n]:
  (5*3**n*Heaviside(n)/3, Abs(z) > 3, True)
[1]  _z_properties_inverse f[n]: (5*3**n*Heaviside(n)/3, Abs(z) > 3, True)
[0]   prop f[n]: (5*3**n*Heaviside(n)/3, Abs(z) > 3, True)
  term_k[n]: (5*3**n*Heaviside(n)/3, Abs(z) > 3, True)

 f[n]: 3*2**n*Heaviside(n)/2 + 5*3**n*Heaviside(n)/3 - 19*DiracDelta(n)/6
 f[n]: (9*2**n + 10*3**n)*Heaviside(n)/6 - 19*DiracDelta(n)/6
f[n] : (9*2**n + 10*3**n)*Heaviside(n)/6 - 19*DiracDelta(n)/6
>>>