Publicado en

2Eva2012TI_T3 LTI DT causal, coeficientes de respuesta impulso h[n]

2da Evaluación I Término 2012-2013. 30/Agosto/2012. TELG1001

Tema 3. (30 puntos) Un estudiante de la materia Sistemas Lineales ha determinado que una de las raíces características del sistema LTI-DT causal, que muestra en la siguiente figura, es γ = 1/4, y cuya ecuación de diferencias que relaciona la entrada-salida del mismo está dada por:

y[n] - \frac{5}{4} y[n-1] + \frac{1}{36} y[n-2] + \frac{1}{18} y[n-3] = x[n] - \frac{1}{2} x[n-1]

Determinar:

a. La respuesta impulso h[n] del sistema. Su respuesta deber ser de la forma:

h[n] = a \alpha^n \mu [n] + b \beta^n \mu[n] + c \gamma^n \mu [n]

obtenga entonces los valores pertinentes.

a= b= c=
α= β= γ=

b. ¿Es el sistema BIBO estable?, justifique su respuesta.

Publicado en

2Eva2011TI_T2 LTI DT Determinar H[z] desde bloques

2da Evaluación I Término 2011-2011. 1/Septiembre/2011. TELG1001

Tema 1. (28 puntos) Considere la existencia de un sistema LTI-DT, donde su ROC es |z|<1 , y cuya realización se muesta en la figura.

a. Determinar la expresión de la función de transferencia de la forma racional siguiente:

H(z) = \frac{N(z)}{D(z)} = \frac{a_0 z^3 +a_1 z^2 + a_2 z+a_3}{b_0 z^2 + b_1 z +b_2}

especificando el valor de los coeficienes ak del polinomio del numerador N(z) y bk del polinomio del denominador D(z).

b. Determinar la ecuación de diferencias que relaciona la entrada-salida del mencionado sistema.

c. ¿Qué puede afirmar acerca de la causalidad y estabilidad del referido sistema? Justifique su respuesta.

d. Determinar la respuesta impulso h[n] de dicho sistema LTI-DT.

Publicado en

2Eva2010TI_T1 LTI DT Bloques de H[z] para ecuacion de diferencias

2da Evaluación I Término 2010-2011. 2/Septiembre/2010. TELG1001

Tema 1. (20 puntos) Un estudiante de la materia Sistemas Lineales ha encontrado que el esquema del diagrama de bloques, en el dominio de la frecuencia compleja , que relaciona la entrada-salida de un sistema LTI-DT causal, es el siguiente:

Determinar:

a. La función de transferencia H(z) del mencionado sistema y esquematizar en el plano complejo los polos y ceros. Comente sobre la estabilidad de éste sistema, justificando su respuesta.

b. La respuesta impulso h[n].

c. La ecuación de diferencia de coeficientes constantes que representa al sistema.

d. La respuesta que se obtendría si la excitación es una sinusoide muestreada cos(1500t) con un intervalo de muestreo Ts = 0.0015

Publicado en

2Eva2009TII_T2 LTI DT Dado h[n], y[n] determine x[n]

2da Evaluación II Término 2009-2010. 4/Febrero/2010. TELG1001

Tema 2. (20 puntos) Para el Sistema que se muestra en la siguiente figura, se obtiene la respuesta y[n] cuando la señal de entrada x[n] está dada por:

x[n] = a \delta[n] + b(c)^{n-1} \mu [n-1]

h[n] = 2 \Big( \frac{1}{3} \Big)^n \mu [n-1] y[n] = (-2)^{n} \mu [n-1]

a. Determinar los coeficientes a, b y c que permiten cumplir con la condición entrada-salida del mencionado sistema-

b. Encontrar la ecuación de diferencias (dominio de tiempo discreto)

c. Esquematice la representación canónica del referido sistema.

d. Comente sobre a qué tipo de estabilidad interna pertenece, e indique justificadamente, si el sistema es BIBO estable o no.

Publicado en

1Eva2016TII_T4 LTI DT Sistema 2do orden

1ra Evaluación II Término 2016-2017. 8/Diciembre/2016. TELG1001

Tema 4. (24 puntos) Un estudiante de la materia Sistemas Lineales, ha descubierto que el esquema de diagrama de bloques, en el dominio de tiempo discreto, que describe la relación de entrada salida de un sistema LTI-DT causal es el siguiente:

a. Determinar la ecuacion de diferencias de coeficientes constantes que permite relacionar la entrada-salida del referido sistema causal.

b. Determinar la respuesta impulso h[n] e indique, justificando debidamente su respuesta, si el sistema es con memoria o sin memoria. BIBO estable o no , FIR o IIR.

c. Determinar el valor de la respuesta de paso s[n] para cuando n→∞.

Coordinador: Tama Alberto

Publicado en

1Eva2016TII_T3 LTI DT Sistema 1er orden con constante a

1ra Evaluación II Término 2016-2017. 8/Diciembre/2016. TELG1001

Tema 3. (24 puntos) Un estudiante de la materia Sistemas Lineales, ha descubierto que el esquema de diagrama de bloques, en el dominio de tiempo discreto, que describe la relación de entrada salida de un sistema LTI-DT causal es el siguiente:

a. Escribir la ecuacion de diferencias que relaciona la entrada-salida del pre-citado sistema y determinar la respuesta impulso h[n] y la respuesta de paso s[n] del mismo.

b. El sistema mostrado es ¿Con memoria o sin memoria?, ¿BIBO estable o no?, ¿FIR o IIR? Justifique sus respuestas de manera razonada.

c. Por algún método se ha comprobado que dicho sistema es invertible. Determinar la respuesta impulso del sistema inverso hinv[n] que permite obtener un sistema identidad. Justrificadamente, indique si el sistema inverso es ¿Con memoria o sin memoria?. ¿Causal o no causal?, ¿BIBO estable o no?, ¿FIR o IIR?

d. Elaborar el esquema del diagrama de bloques, en el dominio de tiempo discreto, que describe la relación entrada-salida del sistema inverso.

Coordinador: Tama Alberto

Publicado en

1Eva2016TI_T3 LTI DT h[n] por bloques y respuesta de paso

1ra Evaluación I Término 2016-2017. 30/Junio/2016. TELG1001

Tema 3. (28 puntos) Un estudiante de la materia Sistema Lineales, ha descubierto que el esquema del diagrama de bloques en el dominio de tiempo discreto, que describe la entrada-salida de un sistema LTI-DT causal, es el siguiente:

a. Determine la ecuación de diferencias de coeficientes constantes que permite relacionar la entrada-salida del referido sistema causal.

b. Determinar la respuesta impulso h[n] e indique si el sitema es con memoria o sin memoria, BiBO estable o no. Justitique debidamente su respuesta.

c. Determinar el valor de la respuesta de paso s[n] para cuando n→∞

Coordinador: Tama Alberto

Publicado en

1Eva2014TI_T2 LTI DT en serie

1ra Evaluación I Término 2014-2015. 3/Julio/2014. TELG1001

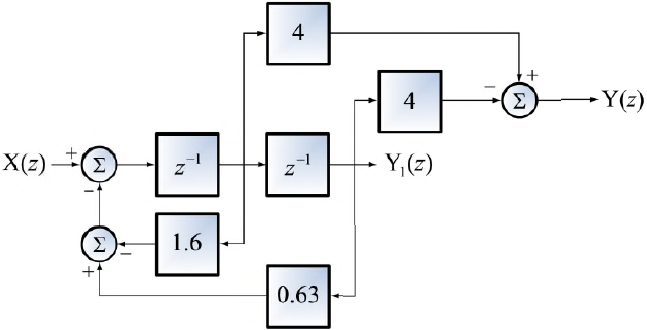
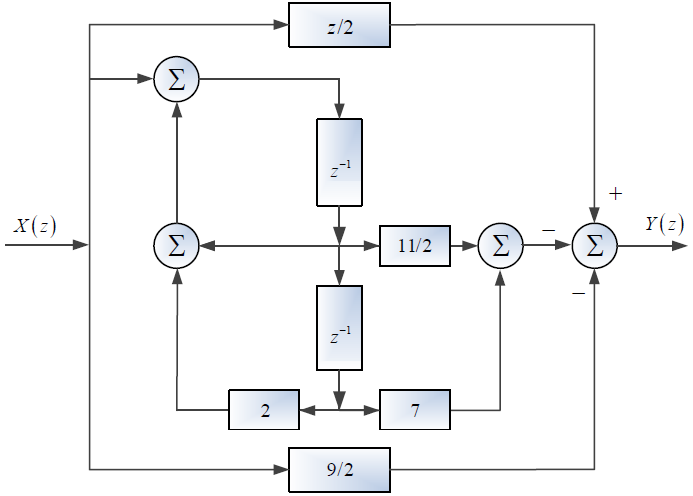
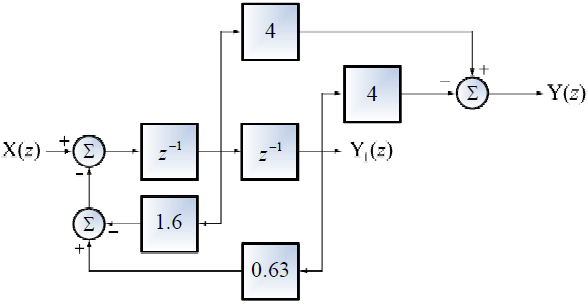
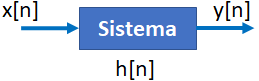
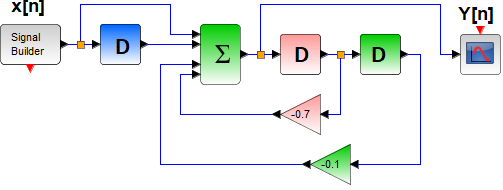
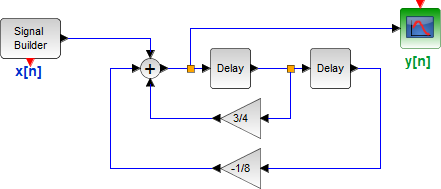
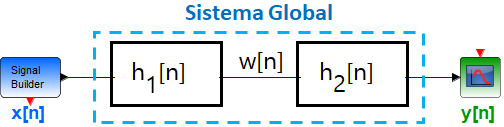
Tema 2. (35 puntos) Con la finalidad de conformar un sistema global, dos sistemas LTI-DT se encuentran conectados en cascada, tal como se muestra en la figura.

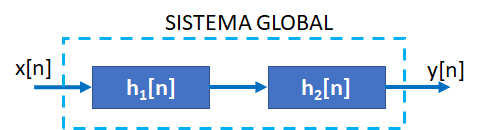
Dichos sistemas están conformados, cada uno de ellos, por dos subsistemas conectados en paralelo.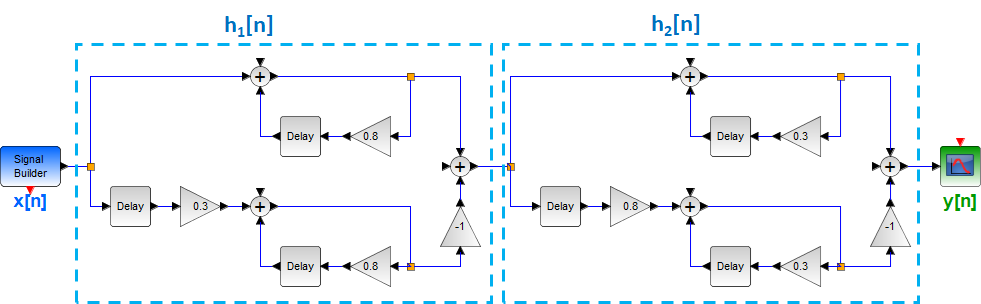 

Al ejecutar el análisis correspondiente, un estudiante de la materia Sistemas Lineales, ha determinado que la respuesta impulso de cada sistema puede ser expresada de la siguiente manera:

h_1 [n] = \alpha ^n \mu [n] - \beta \alpha^{n-1} \mu [n-1] h_2 [n] = \beta ^n \mu [n] - \alpha \beta^{n-1} \mu [n-1]

a. obtener los valores de α y β , e indique la expresión matemática de la respuesta impulso de cada sistema

b. Determinar la respuesta impulso del sistema global e indicar a qeu tipo de sistema pertenece (FIR o IIR).

c. Justificando su respuesta, indique si el sistema global es con Memoria o sin Memoria, causal o no, BiBo estable o no.

d. Determinar, esquematizar y etiquetar la respuesta de dicho sistema, conociendo que la excitación es:

x[n] = \delta[n] - \delta[n-1] +2 \delta [n-3]

Coordinador: Tama Alberto

Publicado en

1Eva2012TII_T2 LTI DT en serie

1ra Evaluación II Término 2012-2013. 29/Noviembre/2012. TELG1001

Tema 2. (25 puntos) Dos sistemas LTI-DT causales, tienen respuesta impulso h1[n] y h2[n] respectivamente. Los sistemas en referencia, utilizados como subsistemas, son conectados en cascada con la finalidad de conformar un sistema global, tal como se muestra en la siguiente figura.

Las ecuaciones de diferencia que relacionan a cada sistema y al global son las siguientes:

S1: w[n] = \frac{1}{2}w[n-1] + x[n] S2: y[n] = \alpha y[n-1] + \beta w[n] SG: y[n] = -\frac{1}{8}y[n-2] + \frac{3}{4}y[n-1] + x[n]

a. Determinar los valores de α y β.

b. Obtener la respuesta impulso del sistema global e indicar a que tipo de sistema pertenece (FIR o IIR)

c. Comente acerca de la estabilidad interna y externa del sistema global. Justifique su respuesta

d. Determinar y esquematizar la respuesta de paso del sistema global.

Coordinador: Tama Alberto

Publicado en

1Eva2012TI_T2 LTI DT en serie

1ra Evaluación I Término 2012-2013. 5/julio/2012. TELG1001

Tema 2. (30 puntos) Dos sistemas LTI-DT tienen respuesta impulso h1[n] y h2[n] respectivamente. Los sistemas en referencia, utilizados como subsistemas, son conectados en cascada con la finalidad de conformar un sistema total, tal como se muestra en la siguiente figura.

h_1 [n] = (0.8)^n \mu [n] - 0.3 (0.8)^{n-1} \mu [n-1] h_2 [n] = (0.3)^n \mu [n] - 0.8 (0.3)^{n-1} \mu [n-1]

a. Determinar la respuesta impulso del sistema total e indicar a qué tipo de sistema pertenece (FIR o IIR).

b. Justificando su respuesta, indique si el sistema es BIBO estable o no.

c. Determinar y esquematizar la respuesta de dicho sistema, conociendo que:

x[n] = \delta [n] - \delta [n-1]

Coordinador: Tama Alberto