[ interpola pulso ] [ pulso rectangular ] [ algoritmo ] [ gráfica interactiva ]
..
1. Interpolación con Pulsos
Referencia: McClellan 4-3.1 p141
Un sistema que convierte una señal y[n] en forma Discreta a la forma Contínua y(t), conocido como D-to-C, usa interpolación para rellenar los espacios entre muestras. En el proceso se deben considerar efectos como el "aliasing" y "folding".
La implementación del concepto D-to-C en un sistema físico o "hardware" se los conoce como Convertidor Digital-Analógico (DAC) que completa los espacios entre muestras con un pulso p(t)
y(t) = \sum_{n=-\infty}^{\infty} y[n] p(t-nTs)[ interpola pulso ] [ pulso rectangular ] [ algoritmo ] [ gráfica interactiva ]
2. Interpolación con Pulso rectangular, Zero-Order Hold
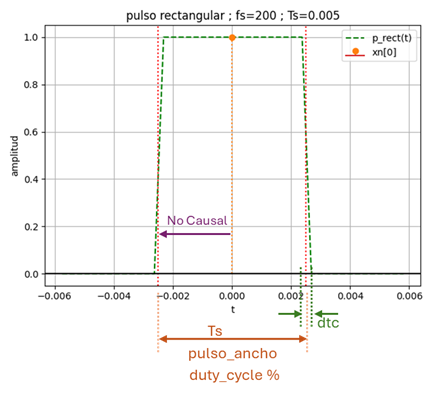
Un pulso simple, simétrico es un pulso rectangular de la forma:
p(t) = \begin{cases} 1 & -\frac{1}{2} T_s \lt t \leq \frac{1}{2} T_s \\ 0 & otro caso \end{cases}
Para una señal senoidad de frecuencia 83Hz y amplitud unitaria se obtienen las muestras x[n]. La frecuencia de muestreo fs es de 200Hz. El proceso de re-construcción de x(t) llena los espacios entre muestras usando el pulso descrito en p(t). En éste caso p(t) es un pulso rectangular.
Los valores de las muestras x[n[ se presentan marcados con puntos para como una referencia en la gráfica.
Si consideramos un muestreo de señal a frecuencia fs=200Hz, se tiene que el pulso tiene una duración Ts = 5 ms y amplitud 1. Cada término de x[n]p(t-nTs) crea una sección plana de amplitud x[n] centrada en nTs, como se muestra en la gráfica.
2.1 Algoritmo en Python para un pulso
# D-to-C, Interpolacion con pulso rectangular # ejemplo 4.3.2 p142 import numpy as np import matplotlib.pyplot as plt # INGRESO fs = 200 # Hz muestreo fs_veces = 16 # suavizar x(t), sobremuestreo titulo = 'pulso rectangular' nT = 2 # graficar periodos de la señal # pulso rectangular pulso_causal = True # No causal, pulso centrado en cero pulso_ancho = 1 dutyc = 1 # entre [0,1] duty_cycle # PROCEDIMIENTO Ts = 1/fs dtc = Ts/fs_veces # suavizar x(t), sobremuestreo #https://blog.espol.edu.ec/telg1001/senales-escalon-%ce%bct-e-impulso-%ce%b4t/ #u = lambda t: np.piecewise(t,t>=0,[1,0]) u = lambda t: np.heaviside(t,1) # pulso rectangular #dutyc = 1 # entre [0,1] duty_cycle u1 = lambda t: u(t+Ts*dutyc/2) u2 = lambda t: u(t-Ts*dutyc/2) rectangular = lambda t: u1(t) - u2(t) # x[n] interpolacion en Ts, a muestreo fs t_unpulso = np.arange(-Ts/2*nT,Ts/2*nT+dtc,dtc) unpulso = rectangular(t_unpulso) # SALIDA print('muestras:',len(t_unpulso)) print('t_unpulso:',t_unpulso) # GRAFICA de un pulso plt.axhline(0,color='Black') plt.axvline(-Ts,color='red',linestyle='dotted') plt.axvline(Ts,color='red',linestyle='dotted') # p(t) componentes plt.plot(t_unpulso,unpulso, color='green',linestyle='dashed', label='p_rect(t)') plt.stem([0],[1],linefmt = 'C1:', label='xn[0]') # grafica entorno plt.xlabel('t') plt.ylabel('amplitud') texto = titulo + ' ; fs='+str(fs) texto = texto +' ; Ts='+str(Ts) plt.title(texto) plt.grid() plt.legend() plt.tight_layout() plt.show()
[ interpola pulso ] [ pulso rectangular ] [ algoritmo ] [ gráfica interactiva ]
..
3. Algoritmo en Python Interpola con pulso rectangular
El algoritmo se divide en:
- cálculo de x(t)
- cálculo de x[n]
- reconstrucción x(t) a partir de x[n] usando pulsos
- gráfica x(t)
- gráfica de x[n]
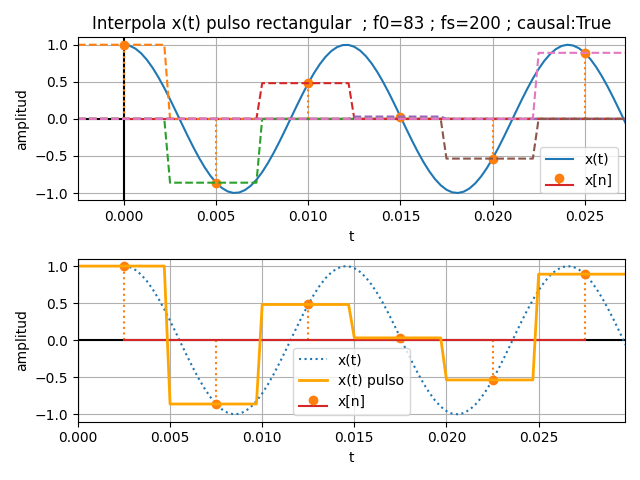
La señal x(t) se convierte a discreta usando una tasa de muestras fs. Para observar la señal x(t), se indica el número de periodos nT de la frecuencia f0. Como ejemplo en la gráfica se realizan nT=2.3 periodos de la señal cosenoidal.
La señal de x(t) se suaviza visualmente al usar el factor fs_veces como sobre-muestreo respecto a fs. En este caso se usa fs=16. lo que genera muestras de señal cada Ts/fs_veces denominado en el algoritmo como tamaño de paso dtc.
Para el relleno de los espacios entre muestras x[n] se usa un modelo de pulso rectangular de tamaño Ts=1/fs que se copia cada vez que se avanza un espacio Ts,
Los valores de tiempo en la gráfica deben considerar la cantidad de muestras x[n], el ancho del pulso, el tiempo de inicio si es o no causal y la frecuencia de muestreo. El proceso se lo agrupa en la función pulso_ti(). El ancho del pulso cambia acorde a la forma del pulso a usar, triangular o Sinc(t). El pulso también se suaviza para la gráfica con fs_veces.
El proceso de reconstrucción de x(t) con pulsos consiste en repetir los valores del vector de un pulso en los tiempos que se dispone de una nueva muestra xki. En el caso que el ancho del pulso sea mayor que 1, los valores de los pulsos se traslapan y se requiere sumar los valores en un solo vector xn_pulsos . El efecto de ésta operación se detalla mejor con las señales triangular y Sinc(t) por tener un ancho de pulso mayor a 1.
Por el momento cada pulso se replica en cada muestra x[n] de la primera figura en la gráfica usando un color diferente. El resultado final de xn_pulsos se presenta en la segunda gráfica como x(t) pulsos.
# D-to-C, Interpolacion con pulso rectangular # ejemplo 4.3.2 p142 import numpy as np import matplotlib.pyplot as plt # INGRESO # señal x(t) f0 = 83 # frecuencia de senal fase0 = 0 # [0,2*np.pi] xt = lambda t: np.cos(2*np.pi*f0*t + fase0) fs = 200 # Hz muestreo fs_veces = 16 # suavizar x(t), sobremuestreo nT = 2.3 # graficar periodos de la señal titulo = 'Interpola x(t) pulso rectangular ' # pulso rectangular pulso_causal = True # No causal, pulso centrado en cero pulso_ancho = 1 dutyc = 1 # entre [0,1] duty_cycle casicero = 1e-10 # cero para valores menores # PROCEDIMIENTO Ts = 1/fs # tamaño de paso con fs T = 1/f0 # periodo de señal dtc = Ts/fs_veces # suavizar x(t), sobremuestreo # muestreo x(t) ti = np.arange(0,nT*T+dtc,dtc) xti = xt(ti) ti_max = max(ti) # muestreo x[n] muestras_n = 2 if ti_max>=Ts: # varias muestras muestras_n = int(ti_max/Ts)+1 ki = np.arange(0,muestras_n,1,dtype=int) tki = ki*Ts # muestras x[n] xki = xt(tki) tkj = tki # x[n] alias0 ti_0 = ti # No Causal, pulso centrado en cero if pulso_causal: # Causal tkj = tki + Ts*pulso_ancho/2 ti_0 = ti + Ts*pulso_ancho/2 xti_0 = xti def pulso_ti(muestras_n,fs,fs_veces,ancho=1,causal=True): ''' tiempos para las n muestras x(t) con pulsos a frecuencia fs. Para suavizar el pulso se usa fs_veces para el sobremuestreo. El ancho del pulso es veces el periodo de muestreo (1/Ts) Si es causal el tiempo inicia en t=0, centrado en cero. Si no es causal el tiempo inicia t en mitad de intervalo. ''' Ts = 1/fs # muestreo periodo dtc = Ts/fs_veces # suavizar pulso(t), sobremuestreo t_Ts = np.arange(0,Ts,dtc) # tiempo en periodo Ts sobremuestreado mitad = Ts*ancho/2 t_mitad = np.arange(0,mitad,dtc) t_pulsos = np.copy(t_mitad) # mitad de primer pulso for i in range(1,muestras_n,1): t_pulsos = np.concatenate((t_pulsos,t_Ts + t_pulsos[-1]+dtc)) # mitad de último pulso para muestra_n t_pulsos = np.concatenate((t_pulsos,t_mitad + t_pulsos[-1]+dtc)) # https://blog.espol.edu.ec/telg1001/sistemas-causales-y-no-causales/ if causal == False: # centrado en cero t_pulsos = t_pulsos - mitad return(t_pulsos) # x[n] interpolacion en Ts, a muestreo fs t_pulsos = pulso_ti(muestras_n,fs,fs_veces, pulso_ancho,pulso_causal) # https://blog.espol.edu.ec/telg1001/senales-escalon-%ce%bct-e-impulso-%ce%b4t/ #u = lambda t: np.piecewise(t,t>=0,[1,0]) u = lambda t: np.heaviside(t,1) # pulso rectangular entre [-(1/fs)/2,(1/fs)/2], no causal u1 = lambda t: u(t+Ts*dutyc/2) u2 = lambda t: u(t-Ts*dutyc/2) rectangular = lambda t: u1(t) - u2(t) # unpulso muestreo t_unpulso = pulso_ti(1,fs,fs_veces, pulso_ancho,pulso_causal) t_pulsoEval= t_unpulso if pulso_causal: t_pulsoEval = t_unpulso-Ts*pulso_ancho/2 unpulso = rectangular(t_pulsoEval) muestras_pulso = len(t_unpulso) # reconstruye x(t) con pulsos muestras_N = len(xki) mitad_pulso = int(muestras_pulso/2) pulsos_vacio = np.zeros(len(t_pulsos),dtype=float) xn_pulsos = np.copy(pulsos_vacio) xk_pulsos = [] for j in range(0,muestras_N,1): # x(t) pulsos k0 = int(j*fs_veces) kn = k0 + muestras_pulso pulsoj = np.copy(pulsos_vacio) pulsoj[k0:kn]= pulsoj[k0:kn] + unpulso*xki[j] xk_pulsos.append(pulsoj) xn_pulsos = xn_pulsos+pulsoj # SALIDA print('fs:',fs,'Hz ; Ts:',Ts,' s') print('pulso_causal:',pulso_causal,' : dutycycle:',dutyc) print('muestras_pulso:',muestras_pulso) print('t_unpulso:',t_unpulso) print('muestras_tiempo:',len(t_pulsos)) # GRAFICAS ---------------------------- fig, [graf_t,graf_n] = plt.subplots(2,1) # x(t) grafico entorno t_causal = 0 if pulso_causal: t_causal = Ts*pulso_ancho/2 graf_t.axhline(0,color='black') graf_t.axvline(0,color='black') graf_t.set_xlabel('t') graf_t.set_ylabel('amplitud') graf_t.set_xlim([t_pulsos[0]-t_causal, t_pulsos[-1]-t_causal]) graf_t.grid() texto = titulo + ' ; f0='+str(f0) texto = texto + ' ; fs='+str(fs) texto = texto + ' ; causal:'+str(pulso_causal) graf_t.set_title(texto) # x(t) componentes graf_t.plot(ti,xti,label='x(t)') graf_t.stem(tki,xki,label='x[n]',linefmt = 'C1:') for i in range(0,muestras_N,1): graf_t.plot(t_pulsos-t_causal,xk_pulsos[i], linestyle='dashed') graf_t.legend() # x[n] grafico entorno graf_n.axhline(0,color='black') graf_n.axvline(0,color='black') graf_n.set_xlabel('t') graf_n.set_ylabel('amplitud') graf_n.set_xlim([t_pulsos[0],t_pulsos[-1]]) graf_n.grid() # x[n] componentes graf_n.plot(ti_0,xti_0,linestyle='dotted', label='x(t)') graf_n.stem(tkj,xki,label='x[n]',linefmt = 'C1:') graf_n.plot(t_pulsos,xn_pulsos, label='x(t) pulso', lw=2, color='orange') graf_n.legend() plt.tight_layout() plt.show()
[ interpola pulso ] [ pulso rectangular ] [ algoritmo ] [ gráfica interactiva ]
..
4. Algoritmo en Python para gráfico interactivo con fs
Para fines didácticos se añade un control en la gráfica para la frecuencia de muestreo fs, con lo que observa mejor el efecto que sub-muestreo, sobre-muestreo y el uso de 2 veces la frecuencia usada en la señal o Nyquist.
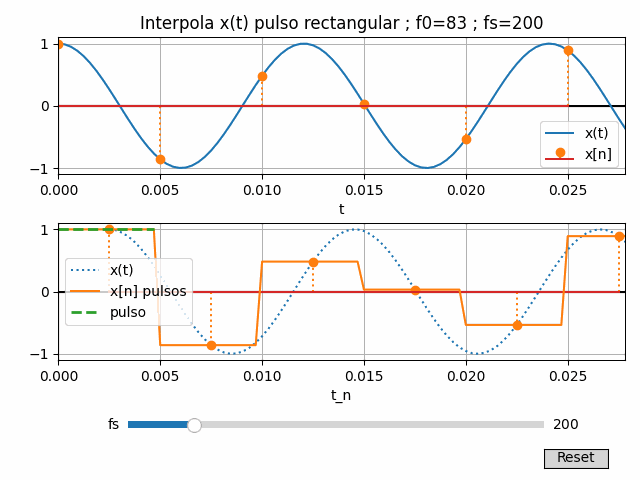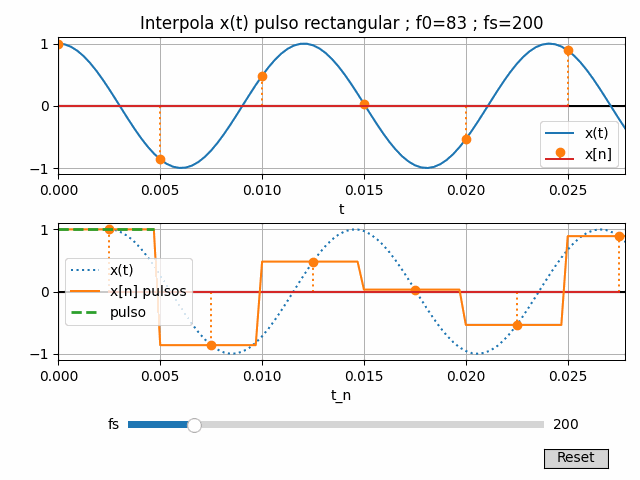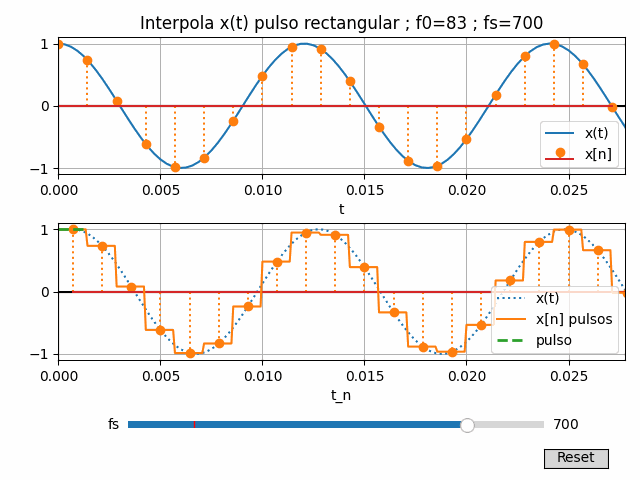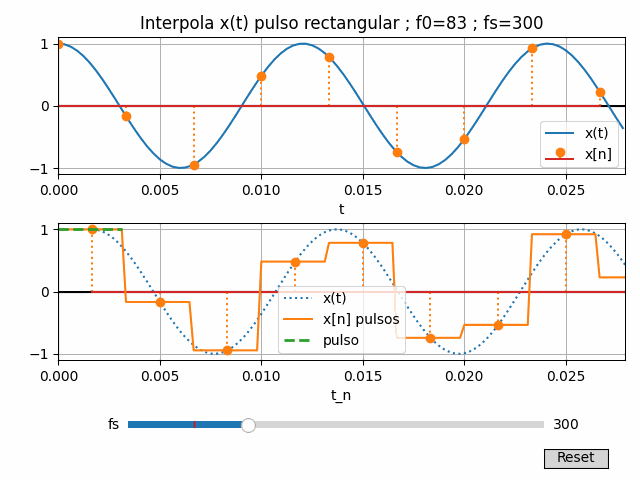Cada cambio de fs tiene efectos sobre las muestras, el ancho de los pulsos y la reconstrucción de x(t). Por tal motivo se agrupan los cálculos de x(t) y x[n] en una función xt_actualiza(), y el proceso de reconstrucción y operaciones con x[n] como la función xn_actualiza().
# D-to-C, Interpolacion con pulso rectangular # grafico interactivo # ejemplo 4.3.2 p142 import numpy as np import matplotlib.pyplot as plt # INGRESO # señal x(t) f0 = 83 # frecuencia de senal fase0 = 0 # [0,2*np.pi] xt = lambda t: np.cos(2*np.pi*f0*t + fase0) fs = 200 # Hz muestreo fs_veces = 16 # suavizar x(t), sobremuestreo nT = 2.3 # graficar periodos de la señal titulo = 'Interpola x(t) pulso rectangular ' # pulso rectangular pulso_causal = True # No causal, pulso centrado en cero pulso_ancho = 1 dutyc = 1 # entre [0,1] duty_cycle casicero = 1e-10 # cero para valores menores # PROCEDIMIENTO Ts = 1/fs # tamaño de paso con fs T = 1/f0 # periodo de señal dtc = Ts/fs_veces # suavizar x(t), sobremuestreo def xt_actualiza(xt,f0,fs,fs_veces,nT, pulso_ancho=1,pulso_causal=True): ''' x(t) muestreada a fs, para nT periodos de x(t). gráfica suavizada con fs_veces. No causal, pulso centrado en cero. Causal el pulso inicia en t=0. ''' Ts = 1/fs # tamaño de paso con fs T = 1/f0 # periodo de señal dtc = Ts/fs_veces # suavizar x(t), sobremuestreo # muestreo x(t) ti = np.arange(0,nT*T+dtc,dtc) xti = xt(ti) ti_max = max(ti) # muestreo x[n] muestras_n = 2 if ti_max>=Ts: # varias muestras muestras_n = int(ti_max/Ts)+1 ki = np.arange(0,muestras_n,1,dtype=int) tki = ki*Ts # muestras x[n] xki = xt(tki) tkj = tki # x[n] alias0 ti_0 = ti # No Causal, pulso centrado en cero if pulso_causal: # Causal tkj = tki + Ts*pulso_ancho/2 ti_0 = ti + Ts*pulso_ancho/2 xti_0 = xti return(ti,xti,tki,xki,tkj,ti_0,xti_0) xt_list = xt_actualiza(xt,f0,fs,fs_veces,nT, pulso_ancho,pulso_causal) [ti,xti,tki,xki,tkj,ti_0,xti_0] = xt_list # x(t),x[n],x(t)_alias0 muestras_n = len(tki) def pulso_ti(muestras_n,fs,fs_veces,ancho=1,causal=True): ''' tiempos para las n muestras x(t) con pulsos a frecuencia fs. Para suavizar el pulso se usa fs_veces para el sobremuestreo. El ancho del pulso es veces el periodo de muestreo (1/Ts) Si es causal el tiempo inicia en t=0, centrado en cero. Si no es causal el tiempo inicia t en mitad de intervalo. ''' Ts = 1/fs # muestreo periodo dtc = Ts/fs_veces # suavizar pulso(t), sobremuestreo t_Ts = np.arange(0,Ts,dtc) # tiempo en periodo Ts sobremuestreado mitad = Ts*ancho/2 t_mitad = np.arange(0,mitad,dtc) t_pulsos = np.copy(t_mitad) # mitad de primer pulso for i in range(1,muestras_n,1): t_pulsos = np.concatenate((t_pulsos,t_Ts + t_pulsos[-1]+dtc)) # mitad de último pulso para muestra_n t_pulsos = np.concatenate((t_pulsos,t_mitad + t_pulsos[-1]+dtc)) # https://blog.espol.edu.ec/telg1001/sistemas-causales-y-no-causales/ if causal == False: # centrado en cero t_pulsos = t_pulsos - mitad return(t_pulsos) def xn_actualiza(fs,fs_veces,xki,dutyc, pulso_ancho=1,pulso_causal=True): ''' x(t) reconstruida con pulsos ''' Ts = 1/fs # tamaño de paso con fs T = 1/f0 # periodo de señal dtc = Ts/fs_veces # suavizar x(t), sobremuestreo #https://blog.espol.edu.ec/telg1001/senales-escalon-e-impulso/ #u = lambda t: np.piecewise(t,t>=0,[1,0]) u = lambda t: np.heaviside(t,1) # pulso rectangular #dutyc = 1 # entre [0,1] duty_cycle u1 = lambda t: u(t+Ts*dutyc/2) u2 = lambda t: u(t-Ts*dutyc/2) rectangular = lambda t: u1(t) - u2(t) # x[n] interpolacion en Ts, a muestreo fs muestras_n = len(xki) t_pulsos = pulso_ti(muestras_n,fs,fs_veces, pulso_ancho,pulso_causal) # unpulso muestreo t_unpulso = pulso_ti(1,fs,fs_veces, pulso_ancho,pulso_causal) t_pulsoEval= t_unpulso if pulso_causal: t_pulsoEval = t_unpulso-Ts*pulso_ancho/2 unpulso = rectangular(t_pulsoEval) muestras_pulso = len(t_unpulso) muestras_N = len(xki) pulsos_vacio = np.zeros(len(t_pulsos),dtype=float) xn_pulsos = np.copy(pulsos_vacio) xk_pulsos = [] for j in range(0,muestras_N,1): # x(t) pulsos k0 = int(j*fs_veces) kn = k0 + muestras_pulso pulsoj = np.copy(pulsos_vacio) pulsoj[k0:kn]= pulsoj[k0:kn] + unpulso*xki[j] xk_pulsos.append(pulsoj) xn_pulsos = xn_pulsos+pulsoj return(t_pulsos,xn_pulsos,t_unpulso,unpulso) xn_list = xn_actualiza(fs,fs_veces,xki,dutyc, pulso_ancho,pulso_causal) [t_pulsos,x_pulsos,t_unpulso,unpulso] = xn_list # x[n] pulsos, pulso # SALIDA print('fs:',fs,'Hz ; Ts:',Ts,' s') print('pulso_causal:',pulso_causal,' : dutycycle:',dutyc) print('muestras_pulso:',len(t_unpulso)) print('t_unpulso:',t_unpulso) print('muestras_tiempo:',len(t_pulsos)) # GRAFICAS interactivas---------------------------- from matplotlib.widgets import Slider, Button, TextBox import telg1034 as dsp graf_dx = 0.12 # margen en eje x fig, [graf_t,graf_n] = plt.subplots(2,1) # x(t) grafico entorno graf_t.axhline(0,color='black') graf_t.set_xlabel('t') graf_t.grid() texto = titulo + ' ; f0='+str(f0) texto = texto +' ; fs='+str(fs) graf_t.set_title(texto) # x(t) componentes linea_xt, = graf_t.plot(ti,xti,label='x(t)') puntos_xn = graf_t.stem(tki,xki,label='x[n]',linefmt = 'C1:') graf_t.set_xlim([t_pulsos[0],ti[-1]]) graf_t.legend() # x[n] grafico entorno graf_n.axhline(0,color='black') graf_n.set_xlabel('t_n') graf_n.grid() # x[n] componentes linea_xt0, = graf_n.plot(ti_0,xti_0,linestyle='dotted', label='x(t)') puntos_xki = graf_n.stem(tkj,xki,linefmt = 'C1:') #, label='x[n]') linea_x_pulsos, = graf_n.plot(t_pulsos,x_pulsos,label='x(t) pulsos') linea_pulso, = graf_n.plot(t_unpulso,unpulso, label='pulso',linestyle='dashed',lw=2) graf_n.set_xlim([t_pulsos[0],ti[-1]]) graf_n.legend() plt.tight_layout() # plt.show() # grafica interactiva plt.subplots_adjust(bottom=0.25) # espacio widgets # slider: barras para valores # amplitud slider [x,y,ancho,alto] fs_donde = plt.axes([0.2, 0.10, 0.65, 0.03]) df_pasos = 5 fs_slider = Slider(fs_donde, 'fs', (f0//df_pasos)*df_pasos, (max([fs,10*f0])+2*df_pasos), valinit = fs, valstep = df_pasos, orientation='horizontal') def grafico_actualiza(val): # actualiza valores x,y fs = fs_slider.val xt_list = xt_actualiza(xt,f0,fs,fs_veces,nT, pulso_ancho,pulso_causal) [ti,xti,tki,xki,tkj,ti_0,xti_0] = xt_list # x(t),x[n],x(t)_alias0 dsp.stem_update(puntos_xn,tki,xki,graf_t) # x[n] dsp.stem_update(puntos_xki,tkj,xki,graf_n) linea_xt0.set_xdata(ti_0) #x(t)_alias0 linea_xt0.set_ydata(xti_0) xn_list = xn_actualiza(fs,fs_veces,xki,dutyc,pulso_ancho,pulso_causal) [t_pulsos,x_pulsos,t_unpulso,unpulso] = xn_list # x[n] pulsos, pulso linea_x_pulsos.set_xdata(t_pulsos) # x[n] pulsos linea_x_pulsos.set_ydata(x_pulsos) linea_pulso.set_xdata(t_unpulso) # pulso lti linea_pulso.set_ydata(unpulso) texto = titulo+' ; f0='+str(f0) texto = texto +' ; fs='+str(fs) graf_t.set_title(texto) graf_t.set_xlim([t_pulsos[0],ti[-1]]) graf_n.set_xlim([t_pulsos[0],ti[-1]]) fig.canvas.draw_idle() # actualiza figura # boton reinicio de gráfica btn_rstdonde = plt.axes([0.85, 0.025, 0.1, 0.04]) btn_rst = Button(btn_rstdonde, 'Reset', hovercolor='0.975') def grafico_reinicia(event): fs_slider.reset() return() # objetos interactivos fs_slider.on_changed(grafico_actualiza) btn_rst.on_clicked(grafico_reinicia) plt.show()
[ interpola pulso ] [ pulso rectangular ] [ algoritmo ] [ gráfica interactiva ]