[ reconstrucción ] [ sobre-muestreo ] [ sub-muestreo ] [ algoritmo ]
[ gráfica ] [ gráfica interactiva ]
..
1. Muestreo y Reconstrucción
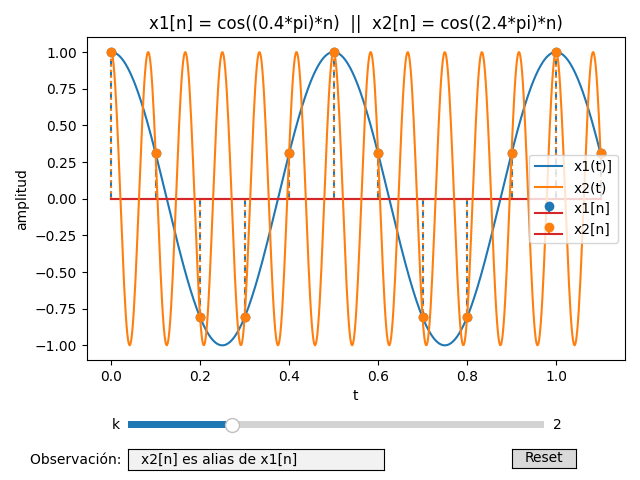
La salida de un convertidor contínuo a discreto C-D es una señal discreta en tiempo con un número infinito de alias. Al observar un gráfico de espectro de frecuencias ω es necesario recordar que existen más señales fuera del intervalo mostrado.
Considere una señal x(t) simple, de una sola frecuencia, cuyo espectro contiene dos líneas a ±ω0 con amplitudes de (1/2 A e±ω0)
x(t) = A cos\Big(\omega_0 t + \varphi \Big)
x[n] = x(n/f_s) A cos((\omega_0 /f_s)*n + \varphi
= \frac{1}{2}A e^{j\varphi}e^{j(\omega_0/f_s)n} + \frac{1}{2}A e^{-j\varphi}e^{j(-\omega_0/f_s)n}
también tiene dos frecuencias ω en ±ω0/fs, con todos los alias en
±ω0/fs + 2πk, siendo k= ±1, ±2, ±3, …
[ reconstrucción ] [ sobre-muestreo ] [ sub-muestreo ] [ algoritmo ]
[ gráfica ] [ gráfica interactiva ]
..
2. Sobre-muestreo
Referencia: McClellan ejercicio 4.5 p133
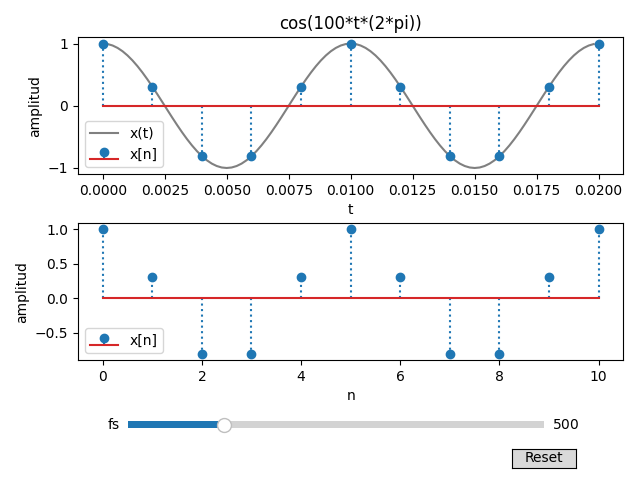
Realice el espectro contínuo de la señal x(t), la señal muestreada a fs=500 y el espectro discreto resultante. Observe que la frecuencia de muestreo es superior a la frecuencia de la señal x(t) para evitar el problema de aliasing. El proceso se conoce como sobre-muestreo. Para el ejercicio se usa una frecuencia 2.5 veces la recomendada por Nyquist.
x(t) = cos\Big(2\pi (100) t + \pi /3 \Big)
Los convertidores D-C trasforman el espectro discreto en tiempo a una salida de espectro contínuo en el tiempo, seleccionando solo un par de las líneas de todas las posibilidades mostradas.
Para ser consistentes con la operación Digital hacia Analógico (D-A) se tomará siempre la frecuencia mas baja de cada grupo de alias o alias principal con |ω|<π.
El resultado siempre se encontrará entre [-fs/2, +fs/2].
En resumen, en sobre-muestreo la frecuencia original f0 es menor que fs/2 permite la reconstrucción mas exacta.
Para el análisis con el algoritmo se obtienen los siguientes parámetros para realizar la gráfica.
eñal(t): cos(((2*pi)*100)*t + pi/3)
espectro_t:
freq : [-100. 100.]
ampl : [1/2 1/2]
fase : [-pi/3 pi/3]
etiq : ['$\\frac{1}{2}$$ e^j(- \\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(\\frac{\\pi}{3})$']
freq_max : 100.0
freq_min : 100.0
muestreo fs: 500 ; dt: 0.002 ; fs_veces: 12
muestreo_tipo: sobre-muestreo
muestreo: 11 tamaño ki: 11 ; tamaño ti: 121
x(t): cos(((2*pi)*100)*t + pi/3)
x[n]: cos(n*(2*pi)/5 + pi/3)
señal[n]: cos(n*(2*pi)/5 + pi/3)
espectro_n:
freq : [-2.4 -1.6 -0.4 0.4 1.6 2.4]
ampl : [1/2 1/2 1/2 1/2 1/2 1/2]
fase : [-pi/3 pi/3 -pi/3 pi/3 -pi/3 pi/3]
etiq : ['$\\frac{1}{2}$$ e^j(- \\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(\\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(- \\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(\\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(- \\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(\\frac{\\pi}{3})$']
x_expand : cos(2*pi*n/5 + pi/3)
freq_factor : pi
freq_max : 2.4
freq_min : 0.4
BW : 2.0
freq_alias : [ True True False False True True]
señal reconstruida con alias principal:
cos(100*t*(2*pi) + pi/3)
Las instrucciones del bloque de ingreso para el algoritmo son:
# INGRESO
with sym.evaluate(False): # no simplificar freq angular w >2*pi por Sympy
x = sym.cos(DosPi*100*t + pi/3)
xt_etiqueta = 'x(t)' ; xn_etiqueta = 'x[n]'
titulo = x # copia para titulo de grafico (antes de procesar)
# señal muestreada
fs = 500 # muestreo discreto, freq_sampling >0
fs_veces = 12 # suavizar x(t), sobremuestreo
muestras_n = 10 + 1 # para x[n]
aliasn = 1 # alias añadidos a x[n]
tolera = 1e-9 # tolerancia a error, números iguales
[ reconstrucción ] [ sobre-muestreo ] [ sub-muestreo ] [ algoritmo ]
[ gráfica ] [ gráfica interactiva ]
..
3. Sub-muestreo y aliasing
Cuando fs < 2f0 la señal se encuentra sub-muestreada y se produce el aliasing. Para el ejercicio anterior, si el ejercicio lo realiza con fs = 80Hz, siendo f0=100 Hz, la tasa de muestreo es menor que la frecuencia de Nyquist y se presenta la señal de alias.
las instrucciones para el bloque de ingreso del algoritmo son las mismas que en el ejercicio anterior, excepto que fs = 80 Hz
# señal muestreada
fs = 80 # muestreo discreto, freq_sampling >0
el resultado con el algoritmo es una señal reconstruida de tan solo 20Hz
x_0(t) = cos\Big(2\pi (20) t + \pi /3 \Big)
señal(t): cos(((2*pi)*100)*t + pi/3)
espectro_t:
freq : [-100. 100.]
ampl : [1/2 1/2]
fase : [-pi/3 pi/3]
etiq : ['$\\frac{1}{2}$$ e^j(- \\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(\\frac{\\pi}{3})$']
freq_max : 100.0
freq_min : 100.0
muestreo fs: 80 ; dt: 0.0125 ; fs_veces: 12
muestreo_tipo: sub-muestreo
muestreo: 11 tamaño ki: 11 ; tamaño ti: 121
x(t): cos(((2*pi)*100)*t + pi/3)
x[n]: cos(5*n*(2*pi)/4 + pi/3)
señal[n]: cos(5*n*(2*pi)/4 + pi/3)
espectro_n:
freq : [-2.5 -1.5 -0.5 0.5 1.5 2.5]
ampl : [1/2 1/2 1/2 1/2 1/2 1/2]
fase : [-pi/3 pi/3 -pi/3 pi/3 -pi/3 pi/3]
etiq : ['$\\frac{1}{2}$$ e^j(- \\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(\\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(- \\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(\\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(- \\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(\\frac{\\pi}{3})$']
x_expand : cos(5*pi*n/2 + pi/3)
freq_factor : pi
freq_max : 2.5
freq_min : 0.5
BW : 2.0
freq_alias : [ True True False False True True]
señal reconstruida con alias principal:
cos(20*t*(2*pi) + pi/3)
[ reconstrucción ] [ sobre-muestreo ] [ sub-muestreo ] [ algoritmo ]
[ gráfica ] [ gráfica interactiva ]
..
4. Folding o plegado de señal por sub-muestreo
Para una señal x(t) de 100 Hz se aplica muestreo insuficiente en el intervalo [f0,2f0] se presenta aliasing denominado «folding» o plegado de señal. Para el ejercicio de prueba y con fs = 125, se tiene:
x(t) = cos\Big(2\pi (100) t + \pi /3 \Big)
Los componentes de frecuencia entre ±π también son ±0.4π, sin embargo el componente en +0.4π es un alias del componente de la frecuencia negativa -1.6π, que genera el «plegado» o «folding». La reconstrucción de la señal se realiza a f = 0.4(fs/2π) = fs/5 = 25 Hz. También se observa una inversión de fase. El resultado es semejante a una señal muestreada de 25 Hz con inversión de fase.
señal(t): cos(((2*pi)*100)*t + pi/3)
espectro_t:
freq : [-100. 100.]
ampl : [1/2 1/2]
fase : [-pi/3 pi/3]
etiq : ['$\\frac{1}{2}$$ e^j(- \\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(\\frac{\\pi}{3})$']
freq_max : 100.0
freq_min : 100.0
muestreo fs: 125 ; dt: 0.008 ; fs_veces: 12
muestreo_tipo: sub-muestreo y folding
muestreo: 11 tamaño ki: 11 ; tamaño ti: 121
x(t): cos(((2*pi)*100)*t + pi/3)
x[n]: cos(4*n*(2*pi)/5 + pi/3)
señal[n]: cos(4*n*(2*pi)/5 + pi/3)
espectro_n:
freq : [-2.4 -1.6 -0.4 0.4 1.6 2.4]
ampl : [1/2 1/2 1/2 1/2 1/2 1/2]
fase : [pi/3 -pi/3 pi/3 -pi/3 pi/3 -pi/3]
etiq : ['$\\frac{1}{2}$$ e^j(\\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(- \\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(\\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(- \\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(\\frac{\\pi}{3})$'
'$\\frac{1}{2}$$ e^j(- \\frac{\\pi}{3})$']
x_expand : cos(8*pi*n/5 + pi/3)
freq_factor : pi
freq_max : 2.4
freq_min : 0.3999999999999999
BW : 2.0
freq_alias : [ True True False False True True]
señal reconstruida con alias principal:
cos(25*t*(2*pi) - (pi/3))
Otro caso a observar es cuando fs=100Hz, el resultado es una constante, pues siempre se obtiene la muestra de la señal con la misma magnitud.
[ reconstrucción ] [ sobre-muestreo ] [ sub-muestreo ] [ algoritmo ]
[ gráfica ] [ gráfica interactiva ]
5. Algoritmo en Python
El algoritmo contiene componentes desarrollados en secciones anteriores. Para el espectro de frecuencias en dominio del tiempo se basa en lo descrito en Espectro – Operaciones en dominio de tiempo y frecuencia.
El desarrollo del muestreo usando la señal x(t) y fs toma como referencia lo descrito en Muestreo y aliasing.
La construcción del espectro discreto a partir de x[n] usa lo desarrollado en Espectro x[n] – Señal discreta en tiempo
# ejercicio 4.5 p133 Muestreo y Reconstrucción de señales sinusoidales
# telg1034 DSP fiec-espol edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
import telg1034 as dsp
# variables continuas
from telg1034 import t,A,w,f,p,pi,DosPi,I,equivalentes
# variables discretas
from telg1034 import n
# INGRESO
with sym.evaluate(False): # no simplificar freq angular w >2*pi por Sympy
x = sym.cos(DosPi*100*t + pi/3)
xt_etiqueta = 'x(t)' ; xn_etiqueta = 'x[n]'
titulo = x # copia para titulo de grafico (antes de procesar)
# señal muestreada
fs = 500 # muestreo discreto, freq_sampling >0
fs_veces = 12 # suavizar x(t), sobremuestreo
muestras_n = 10 + 1 # para x[n]
aliasn = 1 # alias añadidos a x[n]
tolera = 1e-9 # tolerancia a error, números iguales
# PROCEDIMIENTO ----------------
# espectro x(t) - operaciones
# Ref: Blog|Espectro-Operaciones en dominio de tiempo y frecuencia
# unaseñal = x.subs(pi,np.pi) # mantener valores >2pi como float
x_term = dsp.x_list_term_Add(x)
Xe_term = dsp.cos_to_euler_one_term(x_term)
x_term_expand = dsp.euler_to_cos_list(Xe_term)
un_espectro_t = dsp.cos_spectrum_list(x_term)
# espectro de cada señal
freq = un_espectro_t['freq']
ampl = un_espectro_t['ampl']
fase = un_espectro_t['fase']
etiqueta = un_espectro_t['etiq']
# freq_max y freq_min
freq_max = float(max(freq))
if len(freq[freq>0])>0:
freq_min = float(min(freq[freq>0]))
else:
freq_min = 0
un_espectro_t['freq_max'] = freq_max
un_espectro_t['freq_min'] = freq_min
# revisa muestreo Nyquist
if abs(2*freq_max-fs)<tolera:
muestreo_tipo = 'Nyquist'
if fs>(freq_max*2):
muestreo_tipo = 'sobre-muestreo'
if fs<(freq_max*2):
muestreo_tipo = 'sub-muestreo'
if fs<(freq_max*2) and fs>freq_max:
muestreo_tipo = 'sub-muestreo y folding'
# Muestreo de señales sinusoidales
# Ref: blog|Muestreo con Python
xt = sym.lambdify(t,x, modules=equivalentes)
xn = x.subs(t,n/fs)
# muestreo x[n]
dt = 1/fs # tamaño de paso con fs
ki = np.arange(0,muestras_n,1,dtype=int)
tki = ki*dt
xki = xt(tki)
nT = int(np.max(tki)/dt) # periodos a graficar
# muestreo x(t)
dtc = dt/fs_veces # suavizar x(t), sobremuestreo
ti = np.arange(0,(muestras_n-1)*dt+dtc, dtc)
xti = xt(ti)
# operaciones para espectro x[n]
# Ref: blog|Espectro x[n] – Señal discreta en tiempo
#xn = xn.doit()#.subs(pi,np.pi).doit() # mantener valores >2pi
x_term = dsp.x_list_term_Add(xn)
Xe_term = dsp.cos_to_euler_one_term(x_term)
x_term_expand = dsp.euler_to_cos_list(Xe_term)
un_espectro_n = dsp.cos_spectrum_list(x_term)
# espectro de cada señal
freq_n = np.array(un_espectro_n['freq'])
ampl_n = np.array(un_espectro_n['ampl'])
fase_n = np.array(un_espectro_n['fase'])
etiq_n = np.array(un_espectro_n['etiq'])
un_espectro_n['x_expand'] = x_term_expand
freqn_conteo = len(freq_n)
# normaliza w frecuencia angular
for i in range(0,freqn_conteo,1):
while abs(freq_n[i].subs(pi,np.pi))>np.pi:
if freq_n[i]>0:
freq_norm = freq_n[i]-2*pi
else:
freq_norm = freq_n[i]+2*pi
freq_n[i] = freq_norm
# Añadir alias a señal
freqn_alias = np.zeros(freqn_conteo,dtype=bool)
freq_m = np.zeros(0,dtype=float)
for i in range(0,freqn_conteo,1):
freq_i = freq_n[i]
ampl_i = ampl_n[i]
fase_i = fase_n[i]
etiq_i = etiq_n[i]
for k in range(1,aliasn+1,1):
freq_k = (freq_i+2*pi*k)
if not((freq_k in freq_n) or (freq_k in freq_m)):
# añade freq_n[i] + 2*pi*k
freq_m = np.concatenate([freq_m,[freq_i+2*pi*k]])
ampl_n = np.concatenate([ampl_n,[ampl_i]])
fase_n = np.concatenate([fase_n,[fase_i]])
etiq_n = np.concatenate([etiq_n,[etiq_i]])
freqn_alias = np.concatenate([freqn_alias,[True]])
freq_k = (freq_i-2*pi*k)
if not((freq_k in freq_n) or (freq_k in freq_m)):
# añade freq_n[i] - 2*pi*k
freq_m = np.concatenate([freq_m,[freq_i-2*pi*k]])
ampl_n = np.concatenate([ampl_n,[ampl_i]])
fase_n = np.concatenate([fase_n,[fase_i]])
texto = '$' + sym.latex(ampl_i)+'$'
if fase_i!=sym.S.Zero:
texto = texto+f'$ e^j('+sym.latex(fase_i)+')$'
etiq_n = np.concatenate([etiq_n,[texto]])
freqn_alias = np.concatenate([freqn_alias,[True]])
freq_n = np.concatenate([freq_n,freq_m])
# ordena frecuencias
orden = np.argsort(freq_n)
freq_n = freq_n[orden]
ampl_n = ampl_n[orden]
fase_n = fase_n[orden]
etiq_n = etiq_n[orden]
freqn_alias = freqn_alias[orden]
# revisa factor pi en freq_n
unfactor = sym.S.One ; factor_pi = False
freqn_conteo = len(freq_n)
for i in range(0,freqn_conteo,1):
if freq_n[i].has(pi):
factor_pi = True
if factor_pi:
freq_n = np.array(freq_n/pi,dtype=float)
unfactor = pi
# actualiza espectro de señal con factor pi,alias,orden
un_espectro_n['freq_factor'] = unfactor
un_espectro_n['freq'] = freq_n
un_espectro_n['ampl'] = ampl_n
un_espectro_n['fase'] = fase_n
un_espectro_n['etiq'] = etiq_n
# ancho de banda, freq_max y freq_min
freq_posi = freq_n[freq_n>0]
freq_max_n = float(max(freq_posi))
freq_min_n = 0
if len(freq_posi)>0:
freq_min_n = float(min(freq_posi))
freq_centro_n = (freq_max_n + freq_min_n)/2
un_espectro_n['freq_max'] = freq_max_n
un_espectro_n['freq_min'] = freq_min_n
un_espectro_n['BW'] = freq_max_n - freq_min_n
# alias principal, Revisa espectro de frecuencias
freq_conteo = len(freq_n)
freq_alias = np.zeros(freq_conteo,dtype=bool)
for i in range (0,freq_conteo,1):
unafreq = freq_n[i]
if abs(unafreq) > 1:
freq_alias[i] = True
freq_alias_conteo = np.sum(freq_alias)
un_espectro_n['freq_alias'] = freq_alias
# reconstruye señal con alias principal
freq_alias0 = np.invert(freq_alias)
freq_x0 = freq_n[freq_alias0]
ampl_x0 = ampl_n[freq_alias0]
fase_x0 = fase_n[freq_alias0]
x0_cuenta = len(freq_x0)
x0t = sym.S.Zero
for i in range(0,x0_cuenta,1):
if freq_x0[i]>0:
una_freq = float(freq_x0[i]*unfactor*(fs/(2*pi)))
x0t = x0t + 2*ampl_x0[i]*sym.cos(DosPi*una_freq*t+sym.UnevaluatedExpr(fase_x0[i]))
if freq_x0[i]>=0 and freq_x0[i]<tolera: # es cero
una_freq = float(freq_x0[i]*unfactor*(fs/(2*pi)))
x0t = x0t + ampl_x0[i]*sym.cos(DosPi*una_freq*t+sym.UnevaluatedExpr(fase_x0[i]))
x0t = dsp._float_is_int(x0t) # si es entero
x0tr = x0t.subs(pi,np.pi)
if x0tr.has(t): # dos componentes en la constante.
x0tr = sym.lambdify(t,x0tr,modules=equivalentes)
else: # componentes constantes
constante = float(x0tr.doit())
x0tr = lambda t: constante +0*t
x0t = x0t.simplify()
x0_ti = x0tr(ti)
# SALIDA
print('señal(t): ',x)
print(' espectro_t:')
for parametro in un_espectro_t:
print(' ',parametro,':',un_espectro_t[parametro])
print('\nmuestreo fs:',fs,' ; dt:',dt, ' ; fs_veces:',fs_veces)
print('muestreo_tipo: ',muestreo_tipo)
print('muestreo:',muestras_n,
' tamaño ki:',len(ki),'; tamaño ti:',len(ti))
print('x(t):',x)
print('x[n]:',xn)
print('\nseñal[n]: ',xn)
print(' espectro_n:')
for parametro in un_espectro_n:
print(' ',parametro,':',un_espectro_n[parametro])
print('\nseñal reconstruida con alias principal:')
print(x0t)
[ reconstrucción ] [ sobre-muestreo ] [ sub-muestreo ] [ algoritmo ]
[ gráfica ] [ gráfica interactiva ]
..
6. Gráfica
Con los componentes descritos en la parte de algoritmos, se ajustan las gráficas de cada sección para cada sub-gráfica en la figura.
# GRAFICAS ----------------------------------------
# Grafica de espectro de frecuencias
# Ref: blog|Espectro x[n] – Señal discreta en tiempo
graf_dx = 0.12 # margen en eje x
fig_espectro = plt.figure()
# grafica espectro x(t) continuo en tiempo ---------
graf_fasor = fig_espectro.add_subplot(311)
ampl_max = float(max(ampl))
freq_max = float(max(max(freq),fs))*(1+graf_dx/2)
if freq_max!=0:
graf_fasor.set_xlim([-freq_max*(1+graf_dx),
freq_max*(1+graf_dx)])
else:
graf_fasor.set_xlim([-1,1])
graf_fasor.set_ylim([0,ampl_max*(1+graf_dx*4)])
graf_fasor.grid()
graf_fasor.axhline(0,color='black')
graf_fasor.axvline(0,linestyle='dotted',color='grey')
graf_fasor.set_ylabel('Magnitud '+xt_etiqueta)
graf_fasor.set_xlabel('freq Hz', labelpad=0,)
# espectro x(t) continuo en tiempo
graf_fasor.stem(freq,ampl) # grafica espectro magnitud
for k in range(0,len(freq),1): # etiquetas de fasor
graf_fasor.annotate(etiqueta[k],xy=(freq[k],ampl[k]),
xytext=(0,5),textcoords='offset points',ha='center')
# fs frecuencia de muestreo
graf_fasor.stem(fs,ampl_max/2,linefmt = 'C3:', ) # fs
graf_fasor.annotate('fs',xy=(fs,ampl_max/2),
xytext=(0,5),textcoords='offset points',ha='center')
texto = '$' + sym.latex(titulo)+'$' +' ; fs='+str(fs)
texto = texto + ' ; alias='+str(aliasn)
graf_fasor.set_title(texto)
# GRAFICA x(t), x[n], x(t)_alias0 ---------
graf_xt = fig_espectro.add_subplot(312)
graf_xt.set_xlabel('t')
graf_xt.set_ylabel('amplitud')
graf_xt.grid()
graf_xt.plot(ti,xti, color='gray',label='x(t)')
graf_xt.plot(ti,x0_ti, color='blue',label='x(t)_alias0',
linestyle='dotted')
graf_xt.stem(tki,xki,linefmt = 'C0:',label='x[n]_alias0')
graf_xt.legend()
# grafica espectro x[n] de frecuencias discretas---------
# Ref: blog|Espectro x[n] – Señal discreta en tiempo
graf_fasorn = fig_espectro.add_subplot(313)
# grafica x[n] - entorno
freq_n = un_espectro_n['freq']
ampl_n = un_espectro_n['ampl']
etiq_n = un_espectro_n['etiq']
freq_alias = un_espectro_n['freq_alias']
ampl_max = float(max(ampl_n))*(1+graf_dx*4)
freq_max = float(max(un_espectro_n['freq_max'],1))*(1+graf_dx/2)
graf_fasorn.set_xlim([-freq_max,freq_max])
graf_fasorn.set_ylim([min([min(ampl_n),0]),ampl_max])
graf_fasorn.grid()
graf_fasorn.axhline(0,color='black')
graf_fasorn.axvline(0,linestyle='dotted',color='grey')
graf_fasorn.set_ylabel('Magnitud '+xn_etiqueta)
graf_fasorn.set_xlabel('freq rad')
# grafica x[n] - magnitud
freq_alias0 = np.invert(freq_alias)
graf_fasorn.stem(freq_n[freq_alias0],ampl_n[freq_alias0],
linefmt = 'C0--',label = 'alias0')
if len(freq_n[freq_alias])>0:
graf_fasorn.stem(freq_n[freq_alias],ampl_n[freq_alias],
linefmt = 'C1--',label = 'alias')
if un_espectro_n['freq_factor'] != sym.S.One:
unfactor_txt = r'$'+sym.latex(un_espectro_n['freq_factor'])+'$'
freq_etiq = []
for un_num in freq_n:
freq_etiq.append(f''+str(round(un_num,4))+unfactor_txt)
graf_fasorn.set_xticks(ticks=freq_n,labels=freq_etiq)
for k in range(0,len(freq_n),1): # etiquetas de fasor
graf_fasorn.annotate(etiq_n[k],xy=(freq_n[k],ampl_n[k]),
xytext=(0,5),textcoords='offset points',
ha='center')
graf_fasorn.legend()
plt.tight_layout()
plt.show()
[ reconstrucción ] [ sobre-muestreo ] [ sub-muestreo ] [ algoritmo ]
[ gráfica ] [ gráfica interactiva ]
..
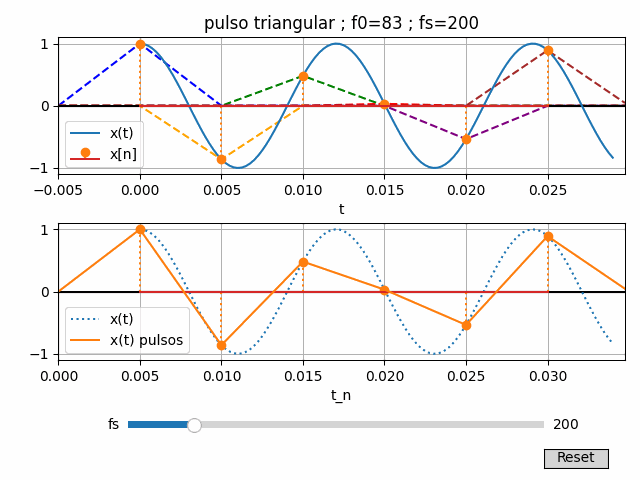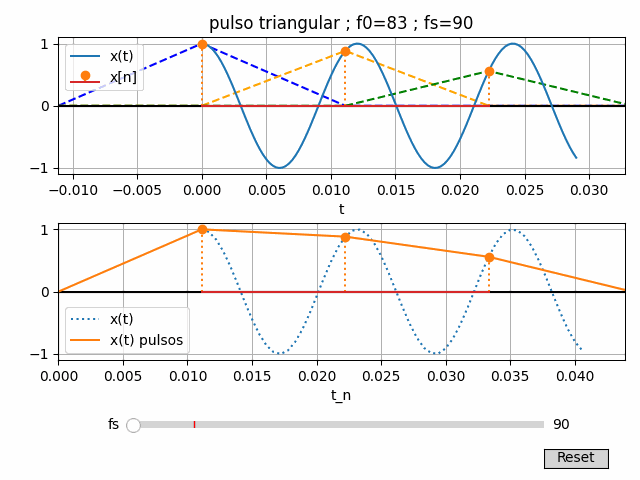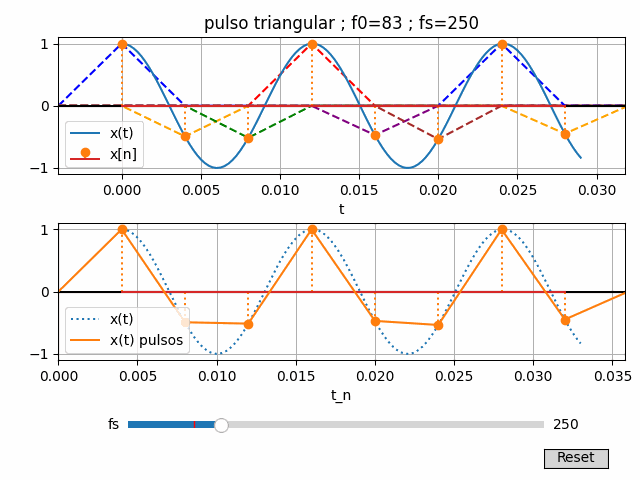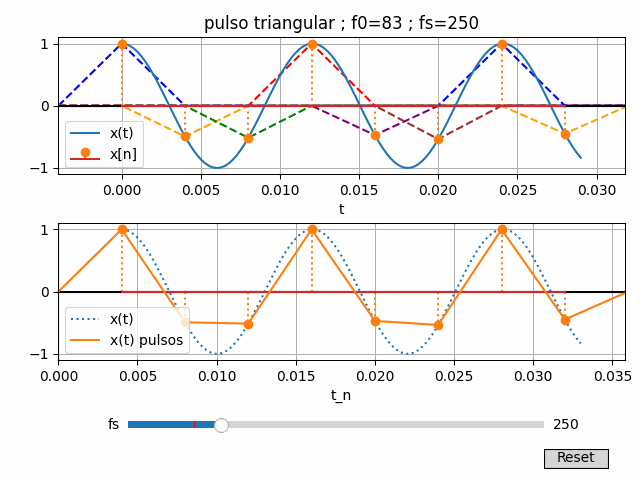
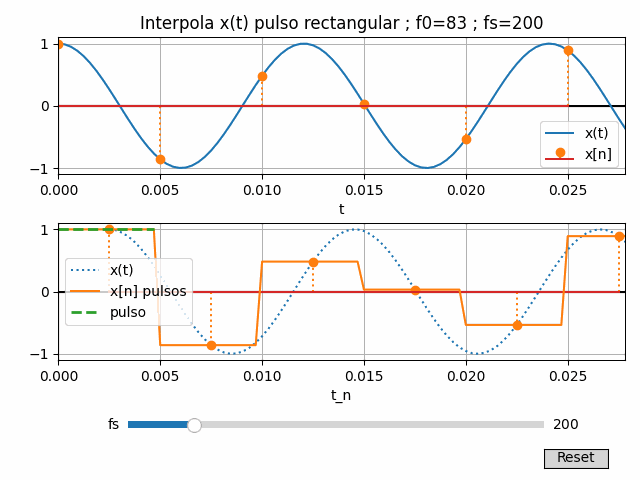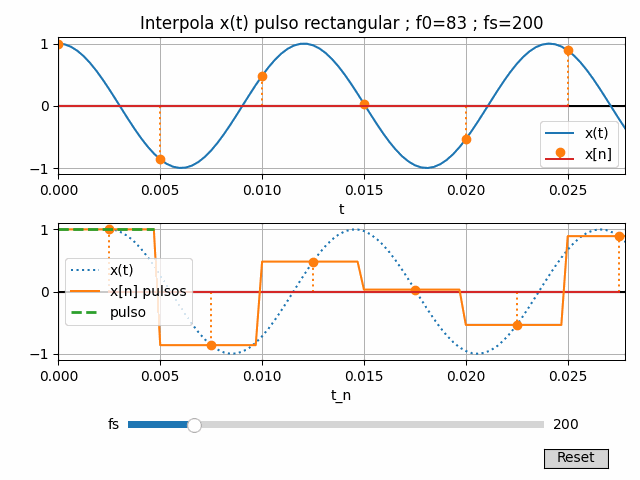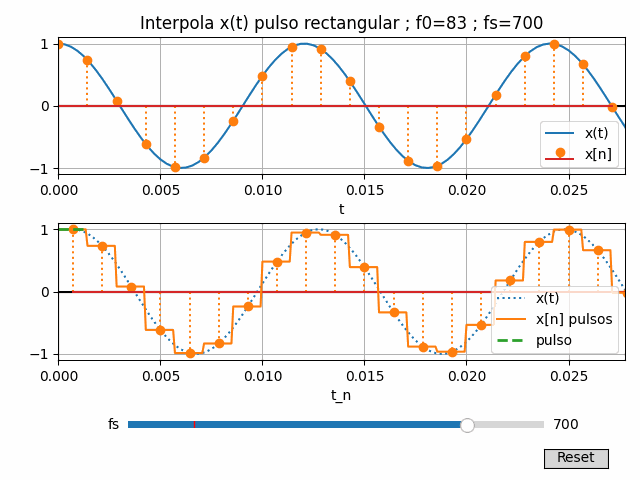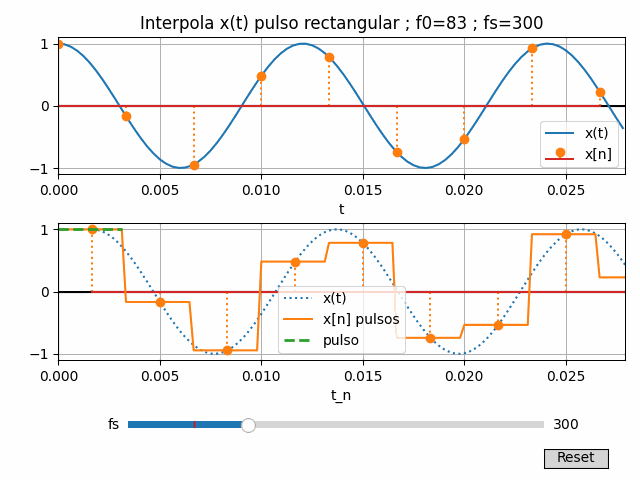
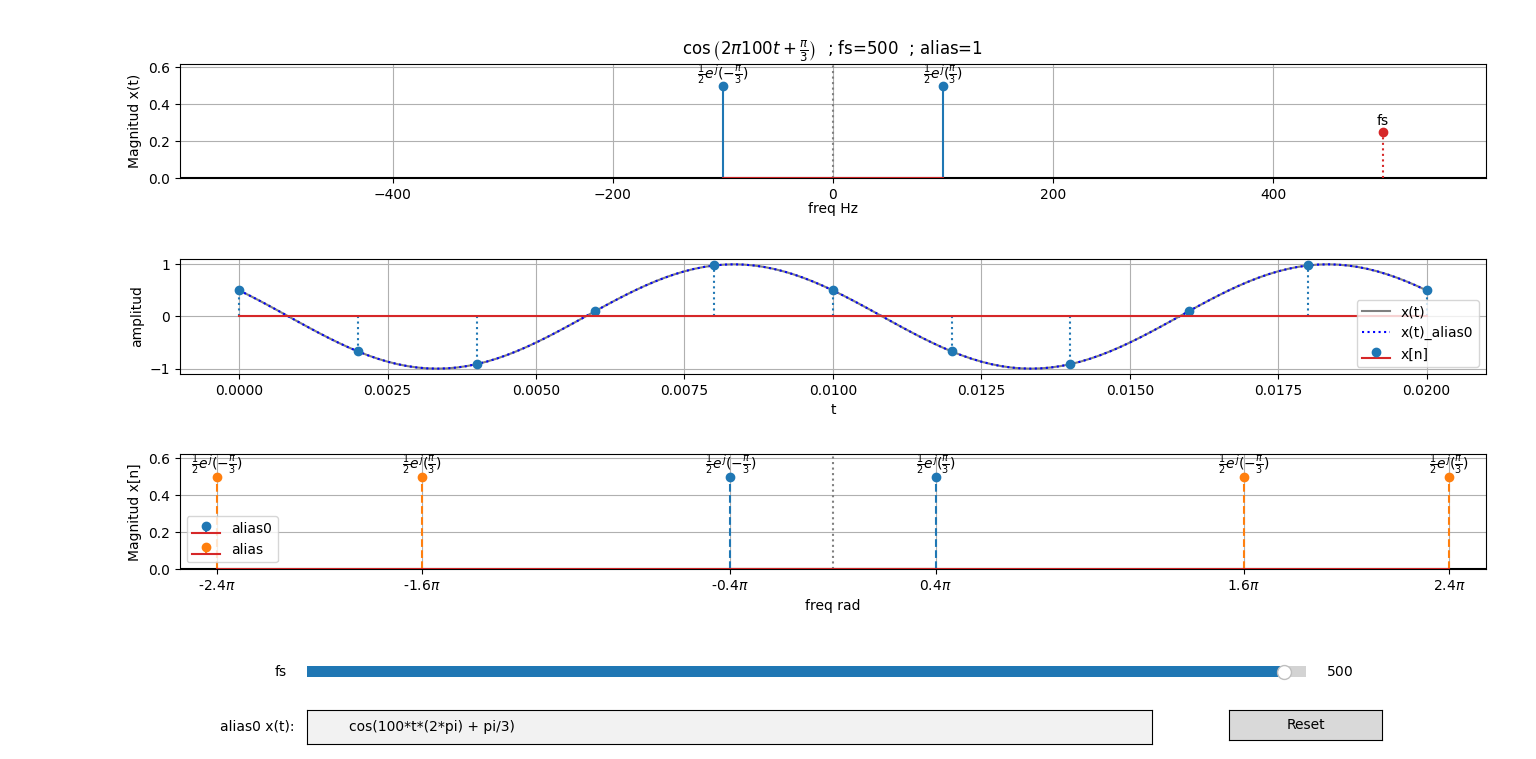
7. Gráfica Interactiva con Python
Se reescribe un poco el algoritmo, agrupando algunos bloques que deben actualizarse al cambiar la variable fs
La frecuencia de muestreo fs se ajusta por medio de una barra de desplazamiento entre los valores de fmax/2 y 2*fmax*+50.
# ejercicio 4.5 p133 Muestreo y Reconstrucción de señales sinusoidales
# grafico interactivo
# telg1034 DSP fiec-espol edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
import telg1034 as dsp
# variables continuas
from telg1034 import t,A,w,f,p,pi,DosPi,I,equivalentes
# variables discretas
from telg1034 import n
# INGRESO
with sym.evaluate(False): # no simplificar freq angular w >2*pi por Sympy
x = sym.cos(DosPi*100*t + pi/3)
xt_etiqueta = 'x(t)' ; xn_etiqueta = 'x[n]'
titulo = x # copia para titulo de grafico (antes de procesar)
# señal muestreada
fs = 500 # muestreo discreto, freq_sampling >0
fs_veces = 12 # suavizar x(t), sobremuestreo
muestras_n = 10 + 1 # para x[n]
aliasn = 1 # alias añadidos a x[n]
tolera = 1e-9 # tolerancia a error, números iguales
# PROCEDIMIENTO ----------------
# espectro x(t) - operaciones
# Ref: Blog|Espectro-Operaciones en dominio de tiempo y frecuencia
# unaseñal = x.subs(pi,np.pi) # mantener valores >2pi como float
x_term = dsp.x_list_term_Add(x)
Xe_term = dsp.cos_to_euler_one_term(x_term)
x_term_expand = dsp.euler_to_cos_list(Xe_term)
un_espectro_t = dsp.cos_spectrum_list(x_term)
# espectro de cada señal
freq = un_espectro_t['freq']
ampl = un_espectro_t['ampl']
fase = un_espectro_t['fase']
etiqueta = un_espectro_t['etiq']
# freq_max y freq_min
freq_max = float(max(freq))
if len(freq[freq>0])>0:
freq_min = float(min(freq[freq>0]))
else:
freq_min = 0
un_espectro_t['freq_max'] = freq_max
un_espectro_t['freq_min'] = freq_min
def sampling_type(fs,freq_max,tolera=1e-9):
'''revisa muestreo Nyquist
'''
if abs(2*freq_max-fs)<tolera:
muestreo_tipo = 'Nyquist'
if fs>(freq_max*2):
muestreo_tipo = 'sobre-muestreo'
if fs<(freq_max*2):
muestreo_tipo = 'sub-muestreo'
if fs<(freq_max*2) and fs>freq_max:
muestreo_tipo = 'sub-muestreo y folding'
return(muestreo_tipo)
muestreo_tipo = sampling_type(fs,freq_max)
# Muestreo de señales sinusoidales
# Ref: blog|Muestreo con Python
xt = sym.lambdify(t,x, modules=equivalentes)
xn = x.subs(t,n/fs)
# muestreo x[n]
dt = 1/fs # tamaño de paso con fs
ki = np.arange(0,muestras_n,1,dtype=int)
tki = ki*dt
xki = xt(tki)
nT = int(np.max(tki)/dt) # periodos a graficar
# muestreo x(t)
dtc = dt/fs_veces # suavizar x(t), sobremuestreo
ti = np.arange(0,(muestras_n-1)*dt+dtc, dtc)
xti = xt(ti)
def espectro_xn_analiza(xn,fs,aliasn):
'''operaciones para espectro x[n]
# Ref: blog|Espectro x[n] – Señal discreta en tiempo
'''
#xn = xn.doit()#.subs(pi,np.pi).doit() # mantener valores >2pi
x_term = dsp.x_list_term_Add(xn)
Xe_term = dsp.cos_to_euler_one_term(x_term)
x_term_expand = dsp.euler_to_cos_list(Xe_term)
un_espectro_n = dsp.cos_spectrum_list(x_term)
# espectro de cada señal
freq_n = np.array(un_espectro_n['freq'])
ampl_n = np.array(un_espectro_n['ampl'])
fase_n = np.array(un_espectro_n['fase'])
etiq_n = np.array(un_espectro_n['etiq'])
un_espectro_n['x_expand'] = x_term_expand
freqn_conteo = len(freq_n)
# normaliza w frecuencia angular
for i in range(0,freqn_conteo,1):
while abs(freq_n[i].subs(pi,np.pi))>np.pi:
if freq_n[i]>0:
freq_norm = freq_n[i]-2*pi
else:
freq_norm = freq_n[i]+2*pi
freq_n[i] = freq_norm
# Añadir alias a señal
freqn_alias = np.zeros(freqn_conteo,dtype=bool)
freq_m = np.zeros(0,dtype=float)
for i in range(0,freqn_conteo,1):
freq_i = freq_n[i]
ampl_i = ampl_n[i]
fase_i = fase_n[i]
etiq_i = etiq_n[i]
for k in range(1,aliasn+1,1):
freq_k = (freq_i+2*pi*k)
if not((freq_k in freq_n) or (freq_k in freq_m)):
# añade freq_n[i] + 2*pi*k
freq_m = np.concatenate([freq_m,[freq_i+2*pi*k]])
ampl_n = np.concatenate([ampl_n,[ampl_i]])
fase_n = np.concatenate([fase_n,[fase_i]])
etiq_n = np.concatenate([etiq_n,[etiq_i]])
freqn_alias = np.concatenate([freqn_alias,[True]])
freq_k = (freq_i-2*pi*k)
if not((freq_k in freq_n) or (freq_k in freq_m)):
# añade freq_n[i] - 2*pi*k
freq_m = np.concatenate([freq_m,[freq_i-2*pi*k]])
ampl_n = np.concatenate([ampl_n,[ampl_i]])
fase_n = np.concatenate([fase_n,[fase_i]])
texto = '$' + sym.latex(ampl_i)+'$'
if fase_i!=sym.S.Zero:
texto = texto+f'$ e^j('+sym.latex(fase_i)+')$'
etiq_n = np.concatenate([etiq_n,[texto]])
freqn_alias = np.concatenate([freqn_alias,[True]])
freq_n = np.concatenate([freq_n,freq_m])
# ordena frecuencias
orden = np.argsort(freq_n)
freq_n = freq_n[orden]
ampl_n = ampl_n[orden]
fase_n = fase_n[orden]
etiq_n = etiq_n[orden]
freqn_alias = freqn_alias[orden]
# revisa factor pi en freq_n
unfactor = sym.S.One ; factor_pi = False
freqn_conteo = len(freq_n)
for i in range(0,freqn_conteo,1):
if freq_n[i].has(pi):
factor_pi = True
if factor_pi:
freq_n = np.array(freq_n/pi,dtype=float)
unfactor = pi
# actualiza espectro de señal con factor pi,alias,orden
un_espectro_n['freq_factor'] = unfactor
un_espectro_n['freq'] = freq_n
un_espectro_n['ampl'] = ampl_n
un_espectro_n['fase'] = fase_n
un_espectro_n['etiq'] = etiq_n
# ancho de banda, freq_max y freq_min
freq_posi = freq_n[freq_n>0]
freq_max_n = float(max(freq_posi))
freq_min_n = 0
if len(freq_posi)>0:
freq_min_n = float(min(freq_posi))
freq_centro_n = (freq_max_n + freq_min_n)/2
un_espectro_n['freq_max'] = freq_max_n
un_espectro_n['freq_min'] = freq_min_n
un_espectro_n['BW'] = freq_max_n - freq_min_n
# alias principal, Revisa espectro de frecuencias
freq_conteo = len(freq_n)
freq_alias = np.zeros(freq_conteo,dtype=bool)
for i in range (0,freq_conteo,1):
unafreq = freq_n[i]
if abs(unafreq) > 1:
freq_alias[i] = True
freq_alias_conteo = np.sum(freq_alias)
un_espectro_n['freq_alias'] = freq_alias
# reconstruye señal con alias principal
freq_alias0 = np.invert(freq_alias)
freq_x0 = freq_n[freq_alias0]
ampl_x0 = ampl_n[freq_alias0]
fase_x0 = fase_n[freq_alias0]
x0_cuenta = len(freq_x0)
x0t = sym.S.Zero
print('freq_alias0',freq_alias0)
print('x0_cuenta',x0_cuenta,fs,pi)
for i in range(0,x0_cuenta,1):
print('i',i,'freq_x0[i]',freq_x0[i],fase_x0[i],ampl_x0[i], unfactor)
if (float(freq_x0[i]))>tolera:
una_freq = float(freq_x0[i]*unfactor*(fs/(2*pi)))
print('una_freq>0',una_freq, unfactor, fs)
x0t = x0t + 2*ampl_x0[i]*sym.cos(DosPi*una_freq*t+sym.UnevaluatedExpr(fase_x0[i]))
if freq_x0[i]>=0 and freq_x0[i]<tolera: # es cero
una_freq = float(freq_x0[i]*unfactor*(fs/(2*pi)))
print('una_freq<tolera',una_freq, unfactor, fs)
x0t = x0t + ampl_x0[i]*sym.cos(DosPi*una_freq*t+sym.UnevaluatedExpr(fase_x0[i]))
print('i',i,'x0t',x0t)
x0t = dsp._float_is_int(x0t) # si es entero
un_espectro_n['x0t'] = x0t
return (un_espectro_n)
un_espectro_n = espectro_xn_analiza(xn,fs,aliasn)
x0t = un_espectro_n['x0t']
x0tr = x0t.subs(pi,np.pi)
if x0tr.has(t): # dos componentes en la constante.
x0tr = sym.lambdify(t,x0tr,modules=equivalentes)
else: # componentes constantes
constante = float(x0tr.doit())
x0tr = lambda t: constante +0*t
x0t = x0t.simplify()
x0_ti = x0tr(ti)
# SALIDA
print('señal(t): ',x)
print(' espectro_t:')
for parametro in un_espectro_t:
print(' ',parametro,':',un_espectro_t[parametro])
print('\nmuestreo fs:',fs,' ; dt:',dt, ' ; fs_veces:',fs_veces)
print('muestreo_tipo: ',muestreo_tipo)
print('muestreo:',muestras_n,
' tamaño ki:',len(ki),'; tamaño ti:',len(ti))
print('x(t):',x)
print('x[n]:',xn)
print('\nseñal[n]: ',xn)
print(' espectro_n:')
for parametro in un_espectro_n:
print(' ',parametro,':',un_espectro_n[parametro])
print('\nseñal reconstruida con alias principal:')
print(x0t)
# GRAFICAS interactivas----------------------------
from matplotlib.widgets import Slider, Button, TextBox
# Grafica de espectro de frecuencias
# Ref: blog|Espectro x[n] – Señal discreta en tiempo
graf_dx = 0.12 # margen en eje x
fig_espectro = plt.figure()
# grafica espectro x(t) continuo en tiempo ---------
# espectro x(t) grafico entorno
graf_fasor = fig_espectro.add_subplot(311)
a_max = float(max(ampl))
f_max = float(max(max(freq),fs))*(1+graf_dx/2)
if f_max!=0:
graf_fasor.set_xlim([-f_max*(1+graf_dx),
f_max*(1+graf_dx)])
else:
graf_fasor.set_xlim([-1,1])
graf_fasor.set_ylim([0,a_max*(1+graf_dx*4)])
graf_fasor.grid()
graf_fasor.axhline(0,color='black')
graf_fasor.axvline(0,linestyle='dotted',color='grey')
graf_fasor.set_ylabel('Magnitud '+xt_etiqueta)
graf_fasor.set_xlabel('freq Hz', labelpad=0,)
# espectro x(t) - componentes
puntos_xt = graf_fasor.stem(freq,ampl) # espectro magnitud
for k in range(0,len(freq),1): # etiquetas de fasor
graf_fasor.annotate(etiqueta[k],xy=(freq[k],ampl[k]),
xytext=(0,5),textcoords='offset points',ha='center')
# espectro x(t) - fs frecuencia de muestreo
puntos_fs = graf_fasor.stem(fs,a_max/2,linefmt = 'C3:', ) # fs
puntos_fs_etiq = graf_fasor.annotate('fs',xy=(fs,(a_max/2)),
xytext=(0,5),textcoords='offset points',ha='center')
texto = '$' + sym.latex(titulo)+'$' +' ; fs='+str(fs)
texto = texto + ' ; alias='+str(aliasn)
graf_fasor.set_title(texto)
# grafica x(t), x[n], x(t)_alias0 --------------
# grafica x(t) - entorno
graf_xt = fig_espectro.add_subplot(312)
graf_xt.set_xlabel('t')
graf_xt.set_ylabel('amplitud')
graf_xt.grid()
# grafica x(t) - componentes
linea_xt, = graf_xt.plot(ti,xti, color='gray',label='x(t)')
linea_xt_a0, = graf_xt.plot(ti,x0_ti, color='blue',
label='x(t)_alias0',linestyle='dotted')
puntos_xn = graf_xt.stem(tki,xki,linefmt = 'C0:',label='x[n]')
graf_xt.legend()
# grafica espectro x[n] de frecuencias discretas---------
# Ref: blog|Espectro x[n] – Señal discreta en tiempo
graf_fasorn = fig_espectro.add_subplot(313)
# grafica x[n] - entorno
freq_n = un_espectro_n['freq']
ampl_n = un_espectro_n['ampl']
etiq_n = un_espectro_n['etiq']
freq_alias = un_espectro_n['freq_alias']
ampl_max = float(max(ampl_n))*(1+graf_dx*4)
w_max = float(max(un_espectro_n['freq_max'],1))*(1+graf_dx/2)
graf_fasorn.set_xlim([-w_max,w_max])
graf_fasorn.set_ylim([min([min(ampl_n),0]),ampl_max])
graf_fasorn.grid()
graf_fasorn.axhline(0,color='black')
graf_fasorn.axvline(0,linestyle='dotted',color='grey')
graf_fasorn.set_ylabel('Magnitud '+xn_etiqueta)
graf_fasorn.set_xlabel('freq rad')
# grafica x[n] - magnitud
freq_alias0 = np.invert(freq_alias)
puntos_alias0 = graf_fasorn.stem(freq_n[freq_alias0],
ampl_n[freq_alias0],
linefmt = 'C0--',label = 'alias0')
if len(freq_n[freq_alias])>0:
puntos_alias = graf_fasorn.stem(freq_n[freq_alias],
ampl_n[freq_alias],
linefmt = 'C1--',label = 'alias')
# actualiza eje x etiquetas
if un_espectro_n['freq_factor'] != sym.S.One:
unfactor_txt = r'$'+sym.latex(un_espectro_n['freq_factor'])+'$'
freq_etiq = []
for un_num in freq_n:
freq_etiq.append(f''+str(round(un_num,4))+unfactor_txt)
graf_fasorn.set_xticks(ticks=freq_n,labels=freq_etiq)
# etiquetas de fasor
a0_etiq = []
for k in range(0,len(freq_n),1):
puntos_a0_etiq = graf_fasorn.annotate(etiq_n[k],
xy=(freq_n[k],ampl_n[k]),
xytext=(0,5),textcoords='offset points',
ha='center')
a0_etiq.append(puntos_a0_etiq)
graf_fasorn.legend()
plt.tight_layout()
# grafica interactiva
plt.subplots_adjust(bottom=0.25) # espacio widgets
# slider: barras para valores
# amplitud slider [x,y,ancho,alto]
fs_donde = plt.axes([0.2, 0.10, 0.65, 0.03])
df_pasos=5
fs_slider = Slider(fs_donde, 'fs',
freq_max/2, (max([fs,2*freq_max])+2*df_pasos),
valinit = fs, valstep = df_pasos,
orientation='horizontal')
txt_xndonde = plt.axes([0.2, 0.02, 0.55, 0.045])
txt_xn = TextBox(txt_xndonde, "alias0 x(t): ",
initial=x0t)
def grafico_actualiza(val):
# actualiza valores x,y
fs = fs_slider.val
# espectro x(t)
dsp.stem_update(puntos_fs,[fs],[ampl_max/2],graf_fasor)
puntos_fs_etiq.xy = (fs, ampl_max/2)
puntos_fs_etiq.set_visible(True)
texto = '$' + sym.latex(titulo)+'$' +' ; fs='+str(fs)
texto = texto + ' ; alias='+str(aliasn)
graf_fasor.set_title(texto)
muestreo_tipo = sampling_type(fs,freq_max)
print(' \n***** fs',fs,muestreo_tipo)
# grafica x(t), x[n] --------------
ti_max = max(ti)
dt = 1/fs
muestras_n=2
if ti_max>=dt:
muestras_n = int(ti_max/dt)+1
ki = np.arange(0,muestras_n,1,dtype=int)
tki = ki*dt
xki = xt(tki)
dsp.stem_update(puntos_xn,tki,xki,graf_xt)
# Nuevo espectro x[n]
xn = x.subs(t,n/fs)
un_espectro_n = espectro_xn_analiza(xn,fs,aliasn)
x0t = un_espectro_n['x0t']
print('x0t:',x0t)
x0tr = x0t.subs(pi,np.pi)
if x0tr.has(t): # dos componentes en la constante.
x0tr = sym.lambdify(t,x0tr,modules=equivalentes)
else: # componentes constantes
constante = float(x0tr.doit())
x0tr = lambda t: constante +0*t
x0t = x0t.simplify()
x0_ti = x0tr(ti)
linea_xt_a0.set_xdata(ti)
linea_xt_a0.set_ydata(x0_ti)
# grafica x[n] - magnitud
freq_alias = un_espectro_n['freq_alias']
freq_alias0 = np.invert(freq_alias)
freq_n = un_espectro_n['freq']
ampl_n = un_espectro_n['ampl']
dsp.stem_update(puntos_alias0,
freq_n[freq_alias0],
ampl_n[freq_alias0],graf_fasorn)
if len(freq_n[freq_alias])>0:
dsp.stem_update(puntos_alias,
freq_n[freq_alias],
ampl_n[freq_alias],graf_fasorn)
if un_espectro_n['freq_factor'] != sym.S.One:
unfactor_txt = r'$'+sym.latex(un_espectro_n['freq_factor'])+'$'
freq_etiq = []
for un_num in freq_n:
freq_etiq.append(f''+str(round(un_num,4))+unfactor_txt)
graf_fasorn.set_xticks(ticks=freq_n,labels=freq_etiq)
# etiquetas de fasor
etiq_n = un_espectro_n['etiq']
for ann in a0_etiq:
ann.remove()
a0_etiq.clear()
for k in range(0,len(freq_n),1):
puntos_a0_etiq = graf_fasorn.annotate(etiq_n[k],
xy=(freq_n[k],ampl_n[k]),
xytext=(0,5),textcoords='offset points',
ha='center')
a0_etiq.append(puntos_a0_etiq)
txt_xn.set_val(x0t)
fig_espectro.canvas.draw_idle() # actualiza figura
# boton reinicio de gráfica
btn_rstdonde = plt.axes([0.8, 0.025, 0.1, 0.04])
btn_rst = Button(btn_rstdonde, 'Reset',
hovercolor='0.975')
def grafico_reinicia(event):
fs_slider.reset()
return()
# objetos interactivos
fs_slider.on_changed(grafico_actualiza)
btn_rst.on_clicked(grafico_reinicia)
plt.show()
[ reconstrucción ] [ sobre-muestreo ] [ sub-muestreo ] [ algoritmo ]
[ gráfica ] [ gráfica interactiva ]
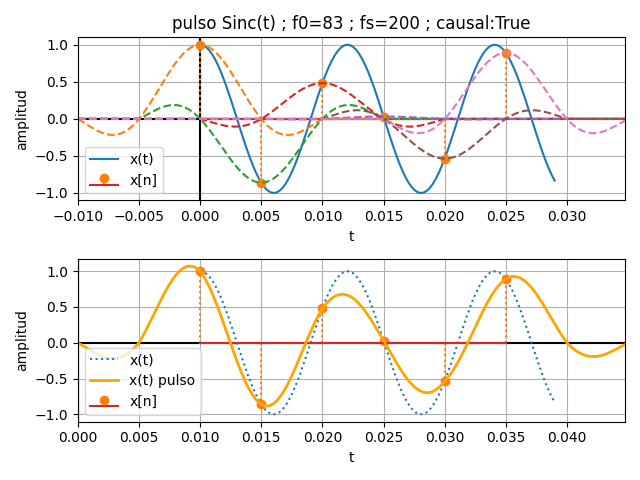[ interpola Sinc ] [ ejemplo ] [ algoritmo ] [ gráfica interactiva ]
