DFT: [ periódicas ] [ freq negativas ] [ simetría conjugada] [ zero_padding ] [ ejemplo_cos ]
..
1. Periódicidad
Referencia: McClellan 8.2.1 p311
La DFT de una secuencia finita de N-puntos es una versión discreta de DTFT:
X[k] = \sum_{n=0}^{N-1} x[n] e^{-j(2\pi k/N)}
= X\Big( e^{j\omega} \Big) \Big|_{\omega=(2\pi k/N)}
= X\Big( e^{j (2\pi k/N)}\Big)
k= 0, 1, …, N-1
Dado que DTFT X(ejω) es siempre periódica con periodo 2π, la DFT X[k] debe ser por lo tanto también periódica. Esto implica que el índice k se mantiene siempre entre 0 y N-1, sin afectar ser evaluado para k≥N o k<0.
Considere que ω + 2π = 2πk/N + 2π(N/N) = 2π(k+N)/N = ωk+N
que implica que los coeficientes X[k] tienen periodo igual a N. Por lo que no se considera necesario más cálculos X[k] fuera del intervalo 0≤k<N.
X[k] = X[k+N]
DFT: [ periódicas ] [ freq negativas ] [ simetría conjugada] [ zero_padding ] [ ejemplo_cos ]
..
2. Frecuencias Negativas y DFT
Referencia: McClellan 8.2.2 p311, 8.2.3.1 p313
Todos los resultados de DFT y IDFT tienen índices no negativos por ser convenientes para los cálculos y expresiones matemáticas. Para la gráfica de espectro de frecuencias se espera utilizar frecuencias positivas y negativas, con simetría en las conjugadas cuando la señal es tipo real.
Cuando la DFT de tamaño N, siendo N par, la transformada X[k] tiene un valor a k=N/2. Cuando N es impar, lo indicado no aplica. El índice k=N/Se corresponde a una frecuencia normalizada ω=2π(N/2)/N)=π. Sin embargo los valores en el espectro son de periodos 2π, siendo ω=-π un alias de ω=π.
Si se realiza la gráfica de forma centrada, la frecuencia esta entre [-π, π]
En Python el desplazamiento de los índices se puede realizar usando np.fft.fftshift() que ubica el centro en la muestra N/2, siempre que N sea par.
DFT: [ periódicas ] [ freq negativas ] [ simetría conjugada] [ zero_padding ] [ ejemplo_cos ]
..
3. Simetría conjugada de DFT
Para una señal x[n] de tipo real, existe la simetría conjugada en la DTFT, los coeficientes deben satisfacer la propiedad:
X[-1] = X*[1]
X[-2] = X*[2]
…
X[-k] = X*[k]
La DFT de una señal real satisface:
X[N-k] = X*[k]
k = 0, 1, …, N-1
DFT: [ periódicas ] [ freq negativas ] [ simetría conjugada] [ zero_padding ] [ ejemplo_cos ]
..
4. Relleno de ceros – Zero Padding
Referencia: McClellan 8.2.4 p314
Para suavizar una gráfica de una DTFT como respuesta de frecuencia, se necesita muestras de frecuencia con tamaños de paso pequeños. De forma implícita, la DFT asume que la longitud o tamaño de la transformada es igual al tamaño o longitud de la señal L, por lo que la DFT de L puntos calcula las muestras de DTFT para (ω=2π/L)k, siendo k=0,1,…,L-1. Las L muestras de frecuencia son con espacios iguales en el intervalo 0≤ω≤2π, con resultado:
H[k] = H \Big( e^{j(2\pi /L)k} \Big) = H \Big( e^{j\omega}\Big) \Big|_{\omega=(2\pi/L)/k}
k = 0, 1, …, L-1
Para disponer de muestras de frecuencia a espacios menores que (2π/N) donde N>L, una forma sencilla es rellenar con ceros o zero-padding. Con lo que la señal se alarga antes de realizar el cálculo para la DFT de N puntos.
h_{zp}[n] = \begin{cases} h[n] & n=\text {0, 1, ..., L-1} \\0 & n= L, L+1, ... , N-1 \end{cases}
4.1 Ejemplo: Respuesta de frecuencias con DFT con zero-padding
Referencia: McClellan 8.4 p315
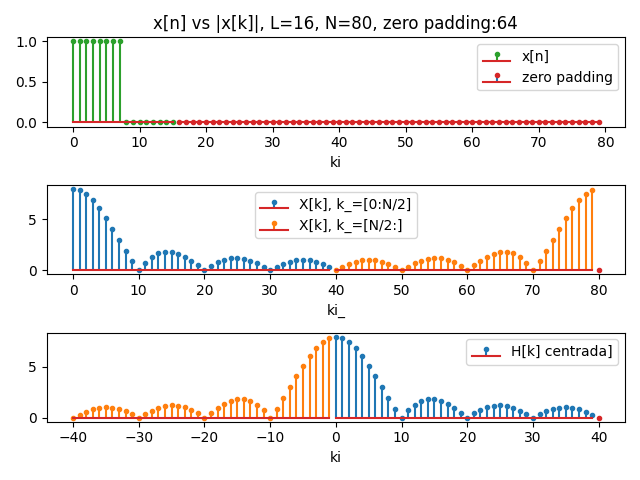
Suponer que requiere una gráfica de respuesta de frecuencia de un filtro FIR de 8 puntos. Para evaluar la respuesta de frecuencia con mejor resolución mediante tamaños de paso mas pequeños entre frecuencias, se usará relleno con ceros o zero-padding, usando un número par en N, por ejemplo N=80.
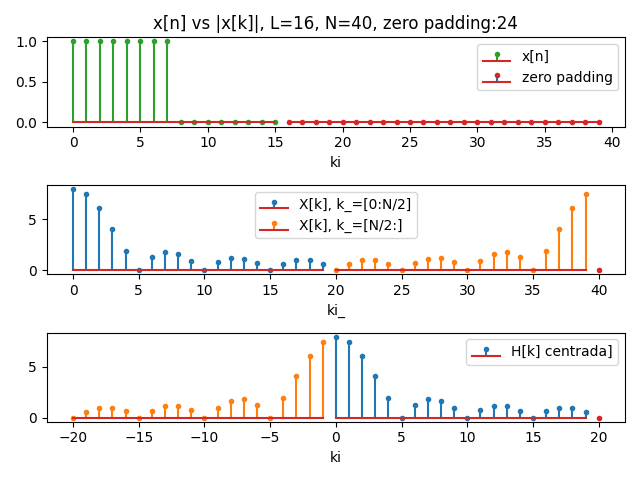
En el caso que N=40, el resultado tiene menor resolución considerando que el intervalo ω se mantiene entre [-π, π]
4.2 Algoritmo en Python
El filtro FIR se puede realizar usando un rectángulo con funciones escalón o Heaviside(n), luego evaluando para las muestras ti.
Para obtener la DFT se usa np.fft.fft(xn, n=N), si n es menor que el tamaño de la señal de entrada, la entrada se trunca. Si es mas grande, se usa zero-padding para completar las muestras. Por lo que la instrucción de Numpy contempla el uso de zero-padding, lo que simplifica el uso del algoritmo presentado de forma didáctica paso a paso.
El centrado del espectro de frecuencias se puede realizar usando un desplazamiento de índices ki_shift.
El resultado del algoritmo, con X[k] centrada, se presenta como:
k0: 0 ; i: 40
freq_Hz: 0.0 ; Xk[k0]: (8+0j)
[ i, freq[ki],|X[k]| ,X[k]]
[0, 0.0, 8.0, (8+0j)]
[1, 0.0125, 7.871076020105053, (7.575558332074842-2.1365284158195137j)]
[2, 0.025, 7.491613901992368, (6.387650908672175-3.914357511197061j)]
[3, 0.037500000000000006, 6.883060301425795, (4.672226464156024-5.054386113140136j)]
...
Instrucciones en Python
# ejemplo 8.4 p315 DFT zero-padding
# telg1034 DSP fiec-espol edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
L = 16 # Tramos en un periodo
# señal es rectangular periódico rect[n]
f0 = 1/16 # frecuencia fundamental de señal
ancho = 0.5*(1/f0) # ancho del impulso rectangular
xt = lambda t: np.heaviside(t,1)-np.heaviside(t-ancho,1)
# para DFT
N = 80 #2*L # N par mayor que L, tramos DFT
# PROCEDIMIENTO
# muestreo de señal x[n]
t0 = 0 ; tn = 1*(1/f0) # intervalo [t0,tn]
dt = (tn-t0)/L
ti = np.arange(t0,tn,dt)
xn = xt(ti)
# verificar que L<=N
if L<=N:
# DFT transformada rapida de Fourier
Xk = np.fft.fft(xn,n=N)
Xkmagn = np.abs(Xk) # para gráfica
Xkfase = np.angle(Xk)
freq_Hz = np.fft.fftfreq(N,dt) # frecuencias en Hz
mitad = int(N/2)
k0 = np.argmax(Xk) # Pico |X[k]|
# ki indices de orden
ki = np.arange(0,N,1)
ki_shift = np.copy(ki)
ki_shift[mitad:] = ki[mitad:]-N
# SALIDA
if N>=L:
print('k0:',k0,'; i:',mitad+k0)
print('freq_Hz:',freq_Hz[k0],
'; Xk[k0]:',Xk[k0])
print('[ i, freq[ki],|X[k]| ,X[k]]')
kmin = k0-4 ; kmax = k0+4
if kmin<0:
kmin = 0
if kmax>N:
kmax = N
for i in range(kmin,kmax,1):
print([i,freq_Hz[i],Xkmagn[i],Xk[i]])
else:
print('Revisar: L debe ser menor o igual a N')
print('L:',L,'; N:',N)
# GRAFICA
if N>=L:
LN_texto= ', L='+str(L)+', N='+str(N)
zp_texto = 'zero padding:'+str(N-L)
plt.subplot(311)
plt.stem(ki[0:len(xn)],np.real(xn),label='x[n]',
markerfmt ='C2.',linefmt='C2-')
if N>L:
kj = np.arange(L,N,dt)
zp = np.zeros(N-L)
plt.stem(kj,zp,label = 'zero padding',
markerfmt ='C3.')
plt.xlabel('ki')
plt.title('x[n] vs |x[k]|'+LN_texto+', '+zp_texto)
plt.legend()
plt.subplot(312)
plt.stem(ki[0:mitad], Xkmagn[0:mitad],
label='X[k], k_=[0:N/2]',
markerfmt ='C0.', linefmt='C0-')
plt.stem(ki[mitad:], Xkmagn[mitad:],
label='X[k], k_=[N/2:]',
markerfmt ='C1.',linefmt='C1-')
plt.stem(N,0,markerfmt ='C3.')
plt.xlabel('ki_')
plt.legend()
plt.subplot(313)
plt.stem(ki_shift[0:mitad], Xkmagn[0:mitad],
label='H[k] centrada]',
markerfmt ='C0.',linefmt='C0-')
plt.stem(ki_shift[mitad:], Xkmagn[mitad:],
markerfmt ='C1.',linefmt='C1-')
plt.stem(mitad,0,markerfmt ='C3.')
plt.xlabel('ki')
plt.legend()
plt.legend()
plt.tight_layout()
plt.show()
DFT: [ periódicas ] [ freq negativas ] [ simetría conjugada] [ zero_padding ] [ ejemplo_cos ]
..
5. DFT de una señal Real tipo Coseno
Referencia: McClellan 8.2.5 p316
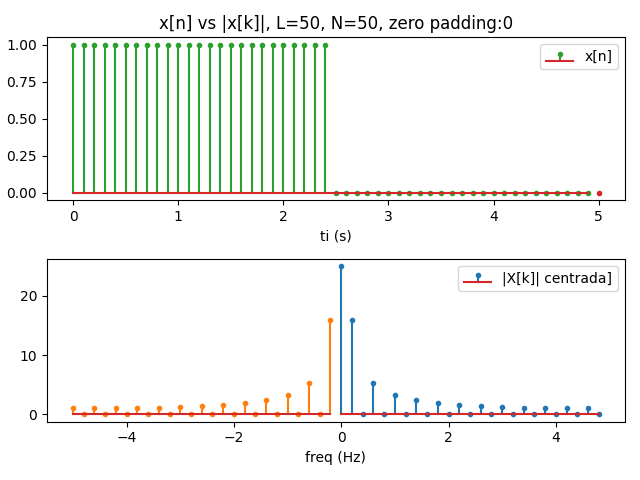
Considere la señal de entrada x[n] coseno, de frecuencia 0.2 de forma discreta para L=50 tramos en tiempo en un intervalo de dos periodos. Para la DFT considere el caso que N=L, no se requiere relleno de ceros.
x[n] = 5 cos(2\pi(0.1)n]
n = 0, 1, …, L-1
Una señal senoidal se puede escribir como la suma de exponenciales complejos y usar la propiedad de linealidad para encontrar el resultado.
El resultado de la DFT muestra la característica de simetría donde ocurre un máximo (pico), en este caso en k=k0=1 y k=N-k0=50-1=49. Las correspondientes frecuencias en Hertz son -0.1 y 0.1. La altura de los picos son aproximadamente AL/2 = 5(50)/2 = 125.
 Resultados numéricos con el algoritmo:
Resultados numéricos con el algoritmo:
k0: 1 ; i: 26
freq_Hz: 0.1 ; Xk[k0]: (125+1.509903313490213e-14j)
[ i, freq[ki],|X[k]| ,X[k]]
[0, 0.0, 9.492406860545088e-15, (9.492406860545088e-15+0j)]
[1, 0.1, 125.0, (125+1.509903313490213e-14j)]
[2, 0.2, 4.842919552269065e-15, (-4.774353709997803e-15-8.120446056592065e-16j)]
[3, 0.30000000000000004, 3.4364294309926203e-15, (2.3207649852950894e-15-2.5343829855056534e-15j)]
[4, 0.4, 2.032850942959038e-15, (8.108973628378316e-16+1.8641159897474457e-15j)]
Para el caso que L<N, el valor de N se aumenta a 8*L, N=400, el resultado del pico de frecuencia se mantiene respecto al caso anterior.
 los resulttados numéricos con el algoritmo son:
los resulttados numéricos con el algoritmo son:
k0: 8 ; i: 208
freq_Hz: 0.1 ; Xk[k0]: (125.00000000000001+1.554312234475219e-14j)
[ i, freq[ki],|X[k]| ,X[k]]
[4, 0.05, 53.33891994969286, (4.999999999999986+53.10405240092081j)]
[5, 0.0625, 75.60689606012141, (33.14721982316793+67.95339984018891j)]
[6, 0.07500000000000001, 96.58278363275512, (70.7485680957908+65.74856809579083j)]
[7, 0.08750000000000001, 113.74232040562568, (105.80156476944595+41.75337523593449j)]
[8, 0.1, 125.00000000000001, (125.00000000000001+1.554312234475219e-14j)]
[9, 0.1125, 128.94638956201757, (119.85004661115146-47.572446945521044j)]
[10, 0.125, 125.00127087574828, (90.85388423989122-85.85388423989122j)]
[11, 0.1375, 113.46542771722382, (47.653106752530654-102.97370879930693j)]
Instrucciones en Python
# ejemplo 8.7 p318 DFT zero-padding cos()
# telg1034 DSP fiec-espol edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
L = 50 # Tramos en un periodo
# señal es rectangular periódico rect[n]
f0 = 0.1 # frecuencia fundamental de señal
xt = lambda t: 5*np.cos(2*np.pi*f0*t)
# para DFT
N = 8*L # N par mayor que L, tramos DFT
# PROCEDIMIENTO
# muestreo de señal x[n]
t0 = 0 ; tn = 1*(1/f0) # intervalo [t0,tn]
dt = (tn-t0)/L
ti = np.arange(t0,tn,dt)
xn = xt(ti)
# verificar que L<=N
if L<=N:
# DFT transformada rapida de Fourier
Xk = np.fft.fft(xn,n=N)
Xkmagn = np.abs(Xk) # para gráfica
Xkfase = np.angle(Xk)
freq_Hz = np.fft.fftfreq(N,dt) # frecuencias en Hz
mitad = int(N/2)
k0 = np.argmax(Xk) # Pico |X[k]|
# SALIDA
if N>=L:
print('k0:',k0,'; i:',mitad+k0)
print('freq_Hz:',freq_Hz[k0],
'; Xk[k0]:',Xk[k0])
print('[ i, freq[ki],|X[k]| ,X[k]]')
kmin = k0-4 ; kmax = k0+4
if kmin<0:
kmin = 0
if kmax>N:
kmax = N
for i in range(kmin,kmax,1):
print([i,freq_Hz[i],Xkmagn[i],Xk[i]])
else:
print('Revisar: L debe ser menor o igual a N')
print('L:',L,'; N:',N)
# GRAFICA
if N>=L:
LN_texto= ', L='+str(L)+', N='+str(N)
zp_texto = 'zero padding:'+str(N-L)
plt.subplot(211)
plt.stem(ti,np.real(xn),label='Re(x[n])',
markerfmt ='C2.',linefmt='C2-')
plt.stem(ti,np.imag(xn),label='Im(x[n])',
markerfmt ='C4.',linefmt='C4:')
if N>L:
tj = np.arange(L*dt,N*dt,dt)
zp = np.zeros(N-L)
plt.stem(tj,zp,label = 'zero padding',
markerfmt ='C3.')
plt.stem(L*dt,0,markerfmt ='C4.')
plt.xlabel('ti (s)')
plt.title('x[n] vs |x[k]|'+LN_texto+', '+zp_texto)
plt.legend()
plt.subplot(212)
plt.stem(freq_Hz[0:mitad], Xkmagn[0:mitad],
label='|X[k]| centrada]',
markerfmt ='C0.',linefmt='C0-')
plt.stem(freq_Hz[mitad:], Xkmagn[mitad:],
markerfmt ='C1.',linefmt='C1-')
plt.xlabel('freq (Hz)')
plt.legend()
plt.legend()
plt.tight_layout()
plt.show()
DFT: [ periódicas ] [ freq negativas ] [ simetría conjugada] [ zero_padding ] [ ejemplo_cos ]


![ifft convolucion rect X[k] H[k] rect](http://blog.espol.edu.ec/telg1034/files/2024/12/ifft_convolucion_rect_X_H_01.png)