[ espectro ] [ ejercicio ] [ analítico ] [ algoritmo ] [ gráfica ]
..
1. Espectro de una suma de sinusoides
Referencia: McClellan 3.1 p70
El método mas general para construir nuevas señales a partir de sinusoides es la combinación lineal, donde una señal se compone de la suma de una constante y N sinusoides, cada una con diferente frecuencia, amplitud y fase.
x(t) = A_0 + \sum_{k =1}^{N} A_k \cos ( 2 \pi f_k t + \varphi_k)que como exponenciales complejos
x(t) = X_0 + \sum_{k =1}^{N} \Re \Big\{ X_k e^{ j 2 \pi f_k t } \Big\} X_k = A_k e^{ \varphi_k }donde X0 = A0 corresponde al componente de una constante real.
La fórmula inversa de Euler permite escribir la señal x(t) como:
x(t) = X_0 + \sum_{k =1}^{N} \Re \Big\{ \frac{X_k}{2} e^{ j 2 \pi f_k t} + \frac{X_k^*}{2} e^{ -j 2 \pi f_k t} \Big\}[ espectro ] [ ejercicio ] [ analítico ] [ algoritmo ] [ gráfica ]
..
2. Ejemplo - Espectro de dos lados
Referencia: McClellan ejemplo 3.1 p71
Determine el espectro de la siguiente señal.
x(t) = 10 + 14 \cos(200 \pi t - \pi/3) + 8 cos(500 \pi t + \pi/2)[ espectro ] [ ejercicio ] [ analítico ] [ algoritmo ] [ gráfica ]
..
3. Desarrollo analítico
La expresión se separa en los componentes de cada término de la suma
x_1(t) = 10 x_2(t) = 14 \cos(200 \pi t - \pi/3) x_3(t) = 8 cos(500 \pi t + \pi/2)se escribe cada término en su forma exponencial
x_1(t) = 10 e^{j0t} = 10 x_2(t) = 7 e^{- j \pi/3} e^{j2\pi(100) t} + 7 e^{j \pi/3} e^{-j 2 \pi (100) t} x_3(t) = 4 e^{- j \pi/2} e^{j 2\pi(250) t} + 4 e^{j \pi/2} e^{-j 2 \pi (250) t}Para la gráfica de espectro de señal se requiere frecuencia, amplitud y fasor, que pueden construir con los parámetros de cada señal usando la función dsp.cos_args_one_term(señal).
El resultado del algoritmo para el ejercicio es:
x_senales:
senal: 10
euler: 10
senal: -8*sin(500*pi*t)
euler: 4*I*exp(500*I*pi*t) - 4*I*exp(-500*I*pi*t)
senal: 14*sin(200*pi*t + pi/6)
euler: 7*exp(-I*pi/3)*exp(200*I*pi*t) + 7*exp(I*pi/3)*exp(-200*I*pi*t)
x_espectro:
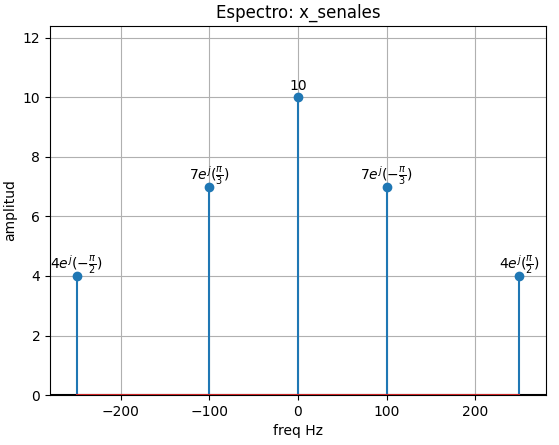
freq : [-250. -100. 0. 100. 250.]
ampl : [4 7 10 7 4]
fase : [-pi/2 pi/3 0 -pi/3 pi/2]
etiq : ['4$ e^j(- \\frac{\\pi}{2})$' '7$ e^j(\\frac{\\pi}{3})$' 10
'7$ e^j(- \\frac{\\pi}{3})$' '4$ e^j(\\frac{\\pi}{2})$']
>>>
[ espectro ] [ ejercicio ] [ analítico ] [ algoritmo ] [ gráfica ]
..
4. Algoritmo con Python
4.1 Señal suma de términos
Para este ejercicio, la señal es una suma de varios componentes: constantes y senoidales.
# INGRESO
x0 = 10
x1 = 14*sym.cos(200*pi*t - pi/3)
x2 = 8*sym.cos(500*pi*t + pi/2)
x = x0 + x1 + x2
Para simplificar el análisis como en los ejercicios anteriores se separan los términos de la suma en una lista x_senales, al revisar si x es una suma x.is_Add:
# Revisa expresión x(t) x = sym.sympify(x) # expresión a sympy, por si es constante x = sym.expand(x) # simplific parentesis (A + 3)*(cos(2*pi*f*t +w)) if x.is_Add: # separa términos suma x_senales = list(x.args) else: x_senales = [x]
Una señal de la x_senales se convierte al formato Euler con las instrucciones
Xj = unasenal.rewrite(sym.exp) # Xj con forma Euler
Xj = sym.expand(Xj)
Por ejemplo, si se usa x1(t), el resultado es la amplitud por la expresión Euler,
>>> x1 14*sin(200*pi*t + pi/6) >>> x1.rewrite(sym.exp) -7*I*(-exp(I*(-200*pi*t - pi/6)) + exp(I*(200*pi*t + pi/6)))
para disponer de términos suma, se simplifica la expresión con:
>>> sym.expand(x1.rewrite(sym.exp)) -7*I*exp(I*pi/6)*exp(200*I*pi*t) + 7*I*exp(-I*pi/6)*exp(-200*I*pi*t) >>>
Si se aplican las instrucciones dadas a cada señal en x_senales, se obtiene X_senales:
x_senales: senal: 10 euler: 10 senal: -8*sin(500*pi*t) euler: 4*I*exp(500*I*pi*t) - 4*I*exp(-500*I*pi*t) senal: 14*sin(200*pi*t + pi/6) euler: 7*exp(-I*pi/3)*exp(200*I*pi*t) + 7*exp(I*pi/3)*exp(-200*I*pi*t)
Sympy simplifica automáticamente e(j π/2) como I y e(-j π/2) como -I
Las instrucciones en Python quedan como:
# ejemplo 3.1 p71 x_senales a formato_euler # telg1034 DSP fiec-espol edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import sympy as sym import telg1034 as dsp # variables from telg1034 import t,A,w,f,p,pi,DosPi,I,equivalentes # INGRESO x0 = 10 x1 = 14*sym.cos(200*pi*t - pi/3) x2 = 8*sym.cos(500*pi*t + pi/2) x = x0 + x1 + x2 # PROCEDIMIENTO # Revisa expresión x(t) x = sym.sympify(x) # expresión a sympy, por si es constante x = sym.expand(x) # simplific parentesis (A + 3)*(cos(2*pi*f*t +w)) if x.is_Add: # separa términos suma x_senales = list(x.args) else: x_senales = [x] # Analiza x_senales x_conteo = len(x_senales) X_senales = [] for i in range(0,x_conteo,1): unasenal = x_senales[i] unasenal = sym.sympify(unasenal) # expresión a sympy, por si es constante cond1 = unasenal.has(t) cond2 = unasenal.has(sym.cos) or unasenal.has(sym.sin) if cond1 and cond2: # tiene variable t y es senoidal if unasenal.has(sym.sin): # evita sin() unasenal = unasenal.rewrite(sym.cos) Xj = unasenal.rewrite(sym.exp) # Xj con forma Euler Xj = sym.expand(Xj) else: # es una constante Xj = unasenal X_senales.append(Xj) # SALIDA print('x_senales: ') for i in range(x_conteo): print('senal: ',x_senales[i]) print(' euler:',X_senales[i])
4.2. Espectro de frecuencia de dos lados
Para realizar la gráfica de espectro de frecuencias, se requiere obtener las listas de frecuencia, amplitud, fase y etiquetas en un diccionario con las listas de valores correspondientes. La creación de la gráfica se simplifica al usar agrupar las instrucciones en una función denominada cos_spectrum_list(x_senales), para obtener los resultados según lo indicado.
Los argumentos de los términos Euler se interpretan como frecuencia, amplitud y fase, se crea euler_args_one_term(X) a partir de lo realizado para la función coseno. Considerando que para la fase es el factor multiplicador con exp() sin variable t, puede ajustarse si aparece un factor con I, o puede considerar el signo en -I.
También, los procedimientos para convertir las señales a la forma Euler, se convierten en funciones de un solo término, cos_to_euler_one_term(x_senales), verificando que cada uno sea SinSumas. En caso de tener sumas se muestra un mensaje que indica los componentes de x_senales que requieran corregirse.
El resultado del algoritmo para el ejercicio es:
x_senales:
senal: 10
euler: 10
senal: -8*sin(500*pi*t)
euler: 4*I*exp(500*I*pi*t) - 4*I*exp(-500*I*pi*t)
senal: 14*sin(200*pi*t + pi/6)
euler: 7*exp(-I*pi/3)*exp(200*I*pi*t) + 7*exp(I*pi/3)*exp(-200*I*pi*t)
x_espectro:
freq : [-250. -100. 0. 100. 250.]
ampl : [4 7 10 7 4]
fase : [-pi/2 pi/3 0 -pi/3 pi/2]
etiq : ['4$ e^j(- \\frac{\\pi}{2})$' '7$ e^j(\\frac{\\pi}{3})$' 10
'7$ e^j(- \\frac{\\pi}{3})$' '4$ e^j(\\frac{\\pi}{2})$']
>>>
Instrucciones en Python
# ejemplo 3.1 p71 x_senales a formato_euler # telg1034 DSP fiec-espol edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import sympy as sym import telg1034 as dsp # variables from telg1034 import t,A,w,f,p,pi,DosPi,I,equivalentes # INGRESO x0 = 10 x1 = 14*sym.cos(200*pi*t - pi/3) x2 = 8*sym.cos(500*pi*t + pi/2) x = x0 + x1 + x2 # PROCEDIMIENTO def x_list_term_Add(x): ''' x(t) separa términos como suma de componentes, simplifica paréntesis ''' x = sym.sympify(x) # expresión a sympy, por si es constante x = sym.expand(x) # simplifica paréntesis (A + 3)*(cos(2*pi*f*t +w)) if x.is_Add: # separa términos suma x_senales = list(x.args) else: x_senales = [x] return(x_senales) def cos_to_euler_one_term(x_senales): ''' convierte lista x_senales a la forma Euler entregando la lista X_senales de cada señal en forma Euler ''' x_conteo = len(x_senales) X_senales = [] SinSumas = True # Analizar un solo cos o sin SinSumas_cual = [] for i in range(0,x_conteo,1): unasenal = x_senales[i] unasenal = sym.sympify(unasenal) # expresión a sympy, por si es constante if unasenal.is_Add: SinSumas = False cond1 = unasenal.has(t) cond2 = unasenal.has(sym.cos) or unasenal.has(sym.sin) if cond1 and cond2 and SinSumas: # tiene variable t y es senoidal if unasenal.has(sym.sin): # evita sin() unasenal = unasenal.rewrite(sym.cos) Xj = unasenal.rewrite(sym.exp) # Xj con forma Euler Xj = sym.expand(Xj) else: # es una constante Xj = unasenal if not(SinSumas): SinSumas_cual.append(i) X_senales.append(Xj) if SinSumas == False: SinSumas_conteo = len(SinSumas_cual) msg ='x_senales tiene '+str(SinSumas_conteo)+'suma de terminos,' msg = msg + 'usar solo un término de la forma:' msg = msg + '\n A*cos(w*t+p) o también A*sin(w*t+p) ... \n' print('cos_to_euler_one_term:',x,msg) for i in SinSumas_cual: print(' revisar: ',x_senales[i]) return(X_senales) def cos_spectrum_list(x_senales): '''dado una lista de señales de un solo término, se obtiene la lista de frecuencias, amplitudes y etiquetas para crear la gráfica de espectro de frecuencias ''' # Analiza x_senales x_conteo = len(x_senales) x_freq_spectr = [] ; x_ampl_spectr = [] x_etiq_spectr = [] ; x_fase_spectr = [] for i in range(0,x_conteo,1): unasenal = x_senales[i] X_senal = unasenal.rewrite(sym.exp) X_senal = sym.expand(X_senal) if X_senal.is_Add: X_senales = X_senal.args else: X_senales = [X_senal] for un_X in X_senales: parametro = euler_args_one_term(un_X) freq_k = float(parametro['freq_Hz']) ampl_k = parametro['amplitud'] fase_k = parametro['fase'] x_freq_spectr.append(freq_k) x_ampl_spectr.append(ampl_k) x_fase_spectr.append(fase_k) texto = '$' + sym.latex(ampl_k)+'$' if fase_k!=sym.S.Zero: texto = texto+f'$ e^j('+sym.latex(fase_k)+')$' x_etiq_spectr.append(texto) # ordenar por freq_Hz x_freq_spectr = np.array(x_freq_spectr) x_ampl_spectr = np.array(x_ampl_spectr) x_etiq_spectr = np.array(x_etiq_spectr) x_fase_spectr = np.array(x_fase_spectr) orden = np.argsort(x_freq_spectr) x_espectro = {'freq':x_freq_spectr[orden], 'ampl':x_ampl_spectr[orden], 'fase':x_fase_spectr[orden], 'etiq':x_etiq_spectr[orden],} return(x_espectro) def euler_args_one_term(X): ''' versión 1. Amplitud, frecuencia en Hz y rad, fase de exp() referenciado a un término coseno. Entrega diccionario con 'amplitud', 'freq_Hz','freq_rad','fase','periodo'. ''' parametro={} # parámetros en diccionario amplitud = sym.S.One ; T = sym.S.Zero ; fase = sym.S.Zero freq_Hz = sym.S.Zero ; freq_rad = sym.S.Zero X = sym.sympify(X) # expresión a sympy, por si es constante X = sym.expand(X) # expresión con al menos una suma SinSumas = True # Analizar un solo exp() if X.is_Add: SinSumas = False if SinSumas: # un solo termino: amplitud*exp(Iw*t+I*p) #X = sym.powsimp(X) partes = X.args if len(partes)==0: # amplitud es una constante. amplitud = X # no tiene args for unaparte in partes: cond1 = unaparte.has(sym.exp) cond2 = unaparte.has(t) if cond1 and cond2: # exp(I*w*t+I*p) argumento_exp = sym.expand(unaparte.args[0]/I) [freq_Hz,freq_rad,fase_k] = dsp._cos_arg_freqfase(argumento_exp) fase = fase + fase_k if cond1 and not(cond2): # exp(p*I) argumento_exp = sym.expand(unaparte.args[0]/I) fase = fase+argumento_exp if not(cond1) and not(cond2): # amplitud if not(unaparte.has(I)): amplitud = amplitud*unaparte else: # amplitud*I o -amplitud*i amplitud = sym.expand(amplitud*unaparte/I) fase = fase + pi/2 if amplitud<0: amplitud = abs(amplitud) fase = fase - pi if not(cond1) and cond2: # I*w*t+I*p argumento_exp = sym.expand(unaparte/I) [freq_Hz,freq_rad,fase] = dsp._cos_arg_freqfase(argumento_exp) # amplitud, revisión numérica if amplitud.is_Number: if amplitud<0: # amplitud con signo positivo amplitud = np.abs(amplitud) fase = fase + sym.pi if isinstance(amplitud,sym.Float): amplitud = float(amplitud) if isinstance(amplitud,sym.Integer): amplitud = int(amplitud) # mantiene forma racional (a/b) de amplitud # periodo T if freq_Hz != sym.S.Zero: T = 1/freq_Hz else: # es una constante T = sym.S.NaN if not(X.has(t)): # es una constante amplitud = X # parametro fasor y fasor_complex fasor = amplitud*sym.exp(I*fase) fasor_complex = sym.expand(fasor,complex=True).evalf() parametro['amplitud'] = amplitud parametro['freq_Hz'] = freq_Hz parametro['freq_rad'] = freq_rad parametro['fase'] = fase parametro['periodo'] = T parametro['fasor'] = fasor parametro['fasor_complex'] = fasor_complex if SinSumas == False: msg ='x(t) tiene suma de terminos, usar solo un término de la forma:' msg = msg + '\n A*exp(I*(w*t+p)) o también A*exp(-I*(w*t+p)) ... \n' print('euler_args_one_term:',x,msg) return(parametro) # operaciones con señal x(t) x_senales = x_list_term_Add(x) x_conteo = len(x_senales) X_senales = cos_to_euler_one_term(x_senales) X_espectro = cos_spectrum_list(x_senales) # SALIDA print('x_senales: ') for i in range(x_conteo): print('senal: ',x_senales[i]) print(' euler:',X_senales[i]) print('x_espectro:') for unparam in X_espectro: print(unparam,':',X_espectro[unparam])
[ espectro ] [ ejercicio ] [ analítico ] [ algoritmo ] [ gráfica ]
..
5. Gráfica de espectro de frecuencias
La gráfica de espectro de frecuencias se obtiene con los datos de x_espectro realizado en el bloque anterior. Se incorpora cada fasor por frecuencia como las etiquetas creada por la función cos_spectrum_list(x_senales).
Instrucciones adicionales para la gráfica
# GRAFICAS de espectro de frecuencias --------- freq = X_espectro['freq'] magnitud = X_espectro['ampl'] etiqueta = X_espectro['etiq'] mag_max = float(max(magnitud)) freq_max = float(max(freq)) # grafica graf_dx = 0.12 fig_espectro = plt.figure() graf_fasor = fig_espectro.add_subplot() # grafica magnitud graf_fasor.set_xlim([-freq_max*(1+graf_dx),freq_max*(1+graf_dx)]) graf_fasor.set_ylim([0,mag_max*(1+graf_dx*2)]) graf_fasor.axhline(0,color='black') graf_fasor.axvline(0,linestyle='dotted',color='grey') graf_fasor.stem(freq,magnitud) # etiquetas de fasor for k in range(0,len(freq),1): texto = etiqueta[k] x_text = freq[k] y_text = magnitud[k] plt.annotate(texto,xy=(x_text,y_text), xytext=(0,5), textcoords='offset points',ha='center') graf_fasor.grid() graf_fasor.set_xlabel('freq Hz') graf_fasor.set_ylabel('amplitud') graf_fasor.set_title('Espectro: x_senales') plt.show()
[ espectro ] [ ejercicio ] [ analítico ] [ algoritmo ] [ gráfica ]