[ interpola Sinc ] [ ejemplo ] [ algoritmo ] [ gráfica interactiva ]
..
1. Interpolación Sinc(t)
Referencia: McClellan 4-3.6 p147
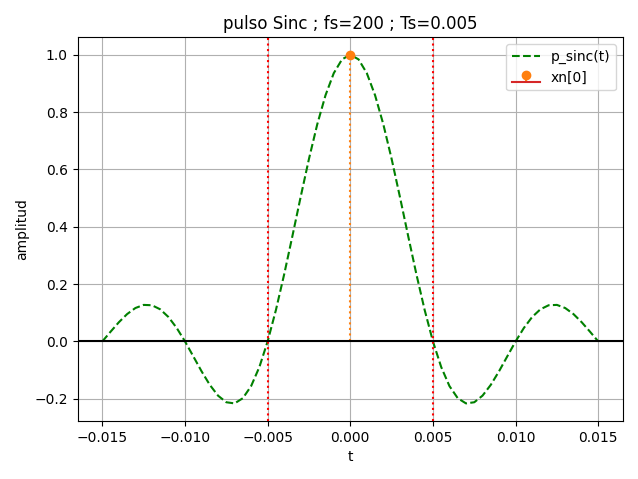
La interpolación con pulso Sinc(t) es un pulso relacionado con la Transformada de Fourier Contínua en tiempo. El pulso Sinc(t) es de ancho infinito y su amplitud disminuye al alejarse de cero, pero no llega a cero o la señal se mantiene en cero.
El valor de p(0)=1 y p(nTs) = 0 para n = ±1, ±2, ±3, ... El tipo de reconstrucción D-to-C es llamada interpolación de banda limitada, al ser equivalente a seleccionar los componentes de alias principal.
Si el muestreo cumple con las condiciones del teorema del muestreo, la reconstrucción de una onda cosenoidal es idéntica a la señal original que generó las muestras.
Una señal contínua x(t) de banda limitada sin componentes de frecuencia mayores a fmax se puede reconstruir exactamente a partir de las muestras x(n Ts), si las muestras se toman a una tasa de fs=1/Ts que es mayor que 2fmax.
[ interpola Sinc ] [ ejemplo ] [ algoritmo ] [ gráfica interactiva ]
2.1 Algoritmo en Python para un pulso Sinc(t)
El algoritmo es el mismo que para un pulso triangular, actualizando la sección de la función que define el pulso.
# D-to-C, Interpolacion con pulso Sinc(t) # ejemplo 4.3.4 p144 import numpy as np import matplotlib.pyplot as plt # INGRESO fs = 200 # Hz muestreo fs_veces = 10 # suavizar x(t), sobremuestreo titulo = 'pulso Sinc' nT = 3.0 # graficar periodos de la señal # pulso Sinc pulso_causal = True # No causal, pulso centrado en cero pulso_ancho = 6 # PROCEDIMIENTO Ts = 1/fs # muestreo periodo dtc = Ts/fs_veces # suavizar x(t), sobremuestreo #https://blog.espol.edu.ec/telg1001/senales-escalon-%ce%bct-e-impulso-%ce%b4t/ #u = lambda t: np.piecewise(t,t>=0,[1,0]) u = lambda t: np.heaviside(t,1) # pulso Sinc u1 = lambda t: u(t+Ts*pulso_ancho/2) u2 = lambda t: u(t-Ts*pulso_ancho/2) sinc = lambda t: (np.sin(np.pi*t/Ts)/(np.pi*t/Ts))*(u1(t) - u2(t)) # x[n] interpolacion en Ts, a muestreo fs t_unpulso = np.arange(-Ts*nT,Ts*nT+dtc,dtc) unpulso = sinc(t_unpulso) # SALIDA print('muestras:',len(t_unpulso)) print('t_unpulso:',t_unpulso) # GRAFICA de un pulso plt.axhline(0,color='black') plt.axvline(-Ts,color='red',linestyle='dotted') plt.axvline(Ts,color='red',linestyle='dotted') # p(t) componentes plt.plot(t_unpulso,unpulso, color='green',linestyle='dashed', label='p_sinc(t)') plt.stem([0],[1],linefmt = 'C1:', label='xn[0]') # grafica entorno plt.xlabel('t') plt.ylabel('amplitud') texto = titulo + ' ; fs='+str(fs) texto = texto +' ; Ts='+str(1/fs) plt.title(texto) plt.grid() plt.legend() plt.tight_layout() plt.show()
[ interpola Sinc ] [ ejemplo ] [ algoritmo ] [ gráfica interactiva ]
..
2. Ejemplo
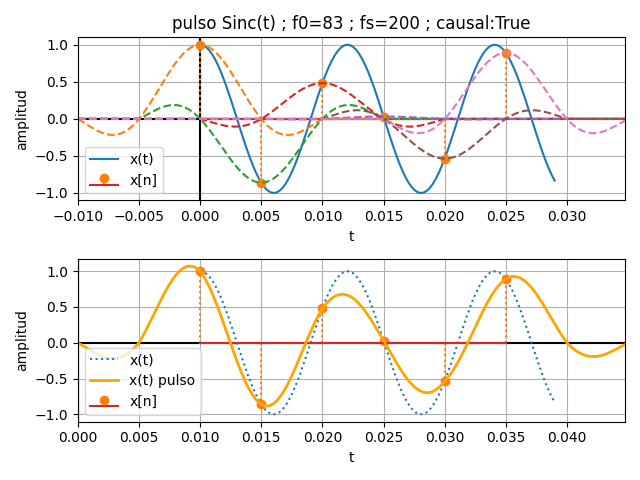
Desarrollar el ejercicio de pulsos triangulares y su algoritmo para realizar la gráfica de la señal sin(2π(83)t) con interpolación de pulsos Sinc(t)
 [ interpola Sinc ] [ ejemplo ] [ algoritmo ] [ gráfica interactiva ]
[ interpola Sinc ] [ ejemplo ] [ algoritmo ] [ gráfica interactiva ]
..
3. Algoritmo en Python Interpola con Sinc
# D-to-C, Interpolacion con pulso Sinc(t) # ejemplo 4.3.4 p144 import numpy as np import matplotlib.pyplot as plt # INGRESO # señal x(t) f0 = 83 # frecuencia de senal fase0 = 0 # [0,2*np.pi] xt = lambda t: np.cos(2*np.pi*f0*t + fase0) fs = 200 # Hz muestreo fs_veces = 20 # suavizar x(t), sobremuestreo nT = 2.4 # graficar periodos de señal x(t) titulo = 'pulso Sinc(t)' # pulso Sinc pulso_causal = True # No causal, centrado en cero pulso_ancho = 4 casicero = 1e-10 # cero para valores menores # PROCEDIMIENTO Ts = 1/fs # tamaño de paso con fs T = 1/f0 # periodo de señal dtc = Ts/fs_veces # suavizar x(t), sobremuestreo # muestreo x(t) ti = np.arange(0,nT*T+dtc,dtc) xti = xt(ti) ti_max = max(ti) # muestreo x[n] muestras_n = 2 if ti_max>=Ts: # varias muestras muestras_n = int(ti_max/Ts)+1 ki = np.arange(0,muestras_n,1,dtype=int) tki = ki*Ts # muestras x[n] xki = xt(tki) tkj = tki # x[n] alias0 ti_0 = ti # No Causal, pulso centrado en cero if pulso_causal: # Causal tkj = tki + Ts*pulso_ancho/2 ti_0 = ti + Ts*pulso_ancho/2 xti_0 = xti def pulso_ti(muestras_n,fs,fs_veces,ancho=1,causal=True): ''' tiempos para las n muestras x(t) con pulsos a frecuencia fs. Para suavizar el pulso se usa fs_veces para el sobremuestreo. El ancho del pulso es veces el periodo de muestreo (1/Ts) Si es causal el tiempo inicia en t=0, centrado en cero. Si no es causal el tiempo inicia t en mitad de intervalo. ''' Ts = 1/fs # muestreo periodo dtc = Ts/fs_veces # suavizar pulso(t), sobremuestreo t_Ts = np.arange(0,Ts,dtc) # tiempo en periodo Ts sobremuestreado mitad = Ts*ancho/2 t_mitad = np.arange(0,mitad,dtc) t_pulsos = np.copy(t_mitad) # mitad de primer pulso for i in range(1,muestras_n,1): t_pulsos = np.concatenate((t_pulsos,t_Ts + t_pulsos[-1]+dtc)) # mitad de último pulso para muestra_n t_pulsos = np.concatenate((t_pulsos,t_mitad + t_pulsos[-1]+dtc)) # https://blog.espol.edu.ec/telg1001/sistemas-causales-y-no-causales/ if causal == False: # centrado en cero t_pulsos = t_pulsos - mitad return(t_pulsos) # x[n] interpolacion en Ts, a muestreo fs t_pulsos = pulso_ti(muestras_n,fs,fs_veces, pulso_ancho,pulso_causal) #https://blog.espol.edu.ec/telg1001/senales-escalon-e-impulso/ #u = lambda t: np.piecewise(t,t>=0,[1,0]) u = lambda t: np.heaviside(t,1) # pulso Sinc(t) # tambien definido como np.sinc() u1 = lambda t: u(t+Ts*pulso_ancho/2) u2 = lambda t: u(t-Ts*pulso_ancho/2) sinc_tl = lambda t: ((np.sin(np.pi*t/Ts)/(np.pi*t/Ts))*(u1(t) - u2(t))) def sinc_t(t): np.seterr(invalid='ignore') # t==0 division para cero resultado = sinc_tl(t) # en t=0, resultado es nan resultado = np.nan_to_num(resultado, nan=1) # cambia nan por 1 return (resultado) # unpulso muestreo t_unpulso = pulso_ti(1,fs,fs_veces, pulso_ancho,pulso_causal) t_pulsoEval= t_unpulso if pulso_causal: t_pulsoEval = t_unpulso-Ts*pulso_ancho/2 unpulso = sinc_t(t_pulsoEval) muestras_pulso = len(t_unpulso) muestras_N = len(xki) mitad_pulso = int(muestras_pulso/2) pulsos_vacio = np.zeros(len(t_pulsos),dtype=float) xn_pulsos = np.copy(pulsos_vacio) xk_pulsos = [] for j in range(0,muestras_N,1): # x[n] pulsos k0 = int(j*fs_veces) kn = k0 + muestras_pulso pulsoj = np.copy(pulsos_vacio) pulsoj[k0:kn]= pulsoj[k0:kn] + unpulso*xki[j] xk_pulsos.append(pulsoj) xn_pulsos = xn_pulsos+pulsoj # SALIDA print('muestras_pulso:',muestras_pulso) print('t_unpulso:',t_unpulso) print('muestras_tiempo:',len(t_pulsos)) # GRAFICAS ---------------------------- fig, [graf_t,graf_n] = plt.subplots(2,1) # x(t) grafico entorno t_causal = 0 if pulso_causal: t_causal = Ts*pulso_ancho/2 graf_t.axhline(0,color='black') graf_t.axvline(0,color='black') graf_t.set_xlabel('t') graf_t.set_ylabel('amplitud') graf_t.set_xlim([t_pulsos[0]-t_causal, t_pulsos[-1]-t_causal]) graf_t.grid() texto = titulo + ' ; f0='+str(f0) texto = texto + ' ; fs='+str(fs) texto = texto + ' ; causal:'+str(pulso_causal) graf_t.set_title(texto) # x(t) componentes graf_t.plot(ti,xti,label='x(t)') graf_t.stem(tki,xki,label='x[n]',linefmt = 'C1:') for i in range(0,muestras_N,1): graf_t.plot(t_pulsos-t_causal,xk_pulsos[i], linestyle='dashed') graf_t.legend() # x[n] grafico entorno graf_n.axhline(0,color='black') graf_n.axvline(0,color='black') graf_n.set_xlabel('t') graf_n.set_ylabel('amplitud') graf_n.set_xlim([t_pulsos[0],t_pulsos[-1]]) graf_n.grid() # x[n] componentes graf_n.plot(ti_0,xti_0,linestyle='dotted', label='x(t)') graf_n.stem(tkj,xki,label='x[n]',linefmt = 'C1:') graf_n.plot(t_pulsos,xn_pulsos, label='x(t) pulso', lw=2, color='orange') graf_n.legend() plt.tight_layout() plt.show()
[ interpola Sinc ] [ ejemplo ] [ algoritmo ] [ gráfica interactiva ]
..
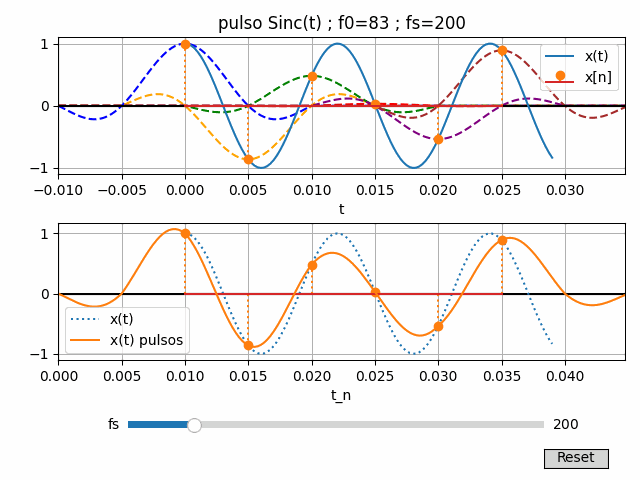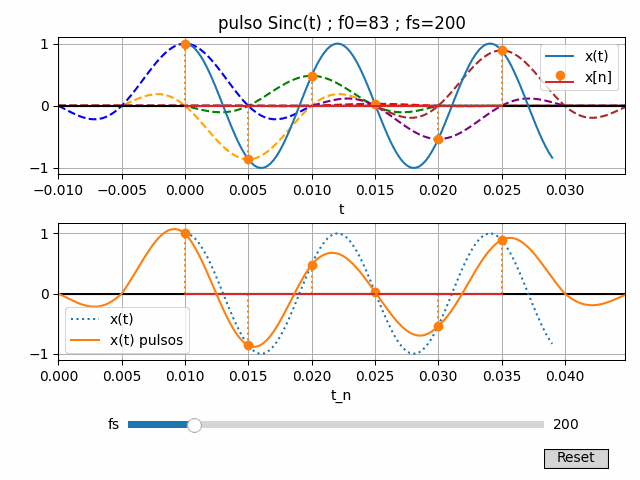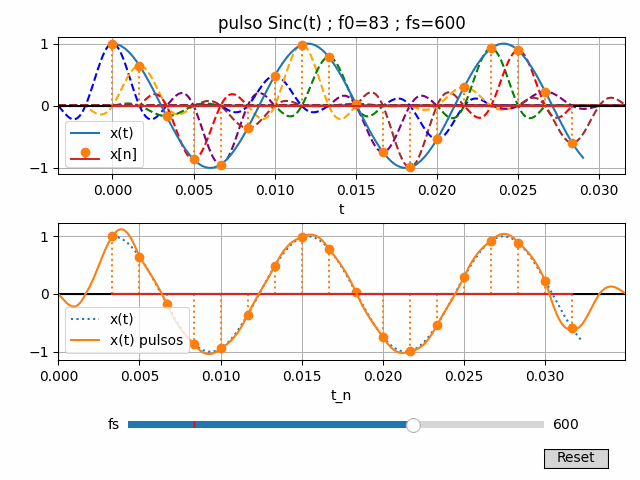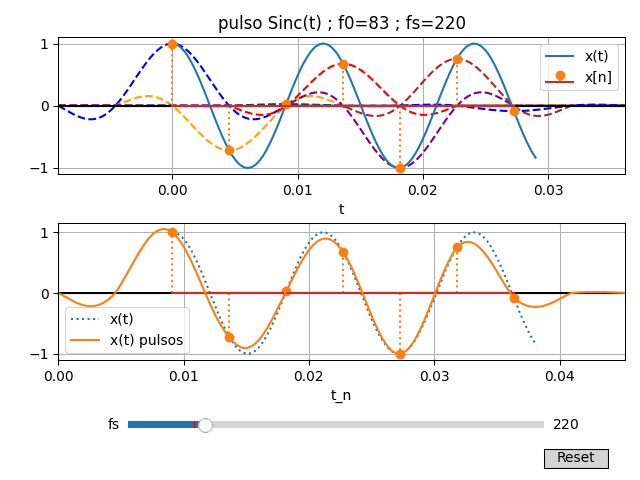
4. Algoritmo en Python para gráfico interactivo con fs
# D-to-C, Interpolacion con pulso Sinc(t) # grafico interactivo # ejemplo 4.3.4 p144 import numpy as np import matplotlib.pyplot as plt # INGRESO # señal x(t) f0 = 83 # frecuencia de senal fase0 = 0 # [0,2*np.pi] xt = lambda t: np.cos(2*np.pi*f0*t + fase0) fs = 200 # Hz muestreo fs_veces = 20 # suavizar x(t), sobremuestreo nT = 2.4 # graficar periodos de señal x(t) titulo = 'pulso Sinc(t)' # pulso Sinc pulso_causal = True # No causal, centrado en cero pulso_ancho = 4 casicero = 1e-10 # cero para valores menores # PROCEDIMIENTO Ts = 1/fs # tamaño de paso con fs T = 1/f0 # periodo de señal dtc = Ts/fs_veces # suavizar x(t), sobremuestreo def xt_actualiza(xt,f0,fs,fs_veces,nT, pulso_ancho=1,pulso_causal=True): ''' x(t) muestreada a fs, para nT periodos de x(t). gráfica suavizada con fs_veces. No causal, pulso centrado en cero. Causal el pulso inicia en t=0. ''' Ts = 1/fs # tamaño de paso con fs T = 1/f0 # periodo de señal dtc = Ts/fs_veces # suavizar x(t), sobremuestreo # muestreo x(t) ti = np.arange(0,nT*T+dtc,dtc) xti = xt(ti) ti_max = max(ti) # muestreo x[n] muestras_n = 2 if ti_max>=Ts: # varias muestras muestras_n = int(ti_max/Ts)+1 ki = np.arange(0,muestras_n,1,dtype=int) tki = ki*Ts # muestras x[n] xki = xt(tki) tkj = tki # x[n] alias0 ti_0 = ti # No Causal, pulso centrado en cero if pulso_causal: # Causal tkj = tki + Ts*pulso_ancho/2 ti_0 = ti + Ts*pulso_ancho/2 xti_0 = xti return(ti,xti,tki,xki,tkj,ti_0,xti_0) xt_list = xt_actualiza(xt,f0,fs,fs_veces,nT, pulso_ancho,pulso_causal) [ti,xti,tki,xki,tkj,ti_0,xti_0] = xt_list # x(t),x[n],x(t)_alias0 muestras_n = len(tki) def pulso_ti(muestras_n,fs,fs_veces,ancho=1,causal=True): ''' tiempos para las n muestras x(t) con pulsos a frecuencia fs. Para suavizar el pulso se usa fs_veces para el sobremuestreo. El ancho del pulso es veces el periodo de muestreo (1/Ts) Si es causal el tiempo inicia en t=0, centrado en cero. Si no es causal el tiempo inicia t en mitad de intervalo. ''' Ts = 1/fs # muestreo periodo dtc = Ts/fs_veces # suavizar pulso(t), sobremuestreo t_Ts = np.arange(0,Ts,dtc) # tiempo en periodo Ts sobremuestreado mitad = Ts*ancho/2 t_mitad = np.arange(0,mitad,dtc) t_pulsos = np.copy(t_mitad) # mitad de primer pulso for i in range(1,muestras_n,1): t_pulsos = np.concatenate((t_pulsos,t_Ts + t_pulsos[-1]+dtc)) # mitad de último pulso para muestra_n t_pulsos = np.concatenate((t_pulsos,t_mitad + t_pulsos[-1]+dtc)) # https://blog.espol.edu.ec/telg1001/sistemas-causales-y-no-causales/ if causal == False: # centrado en cero t_pulsos = t_pulsos - mitad return(t_pulsos) def xn_actualiza(fs,fs_veces,xki, pulso_ancho=1,pulso_causal=True): Ts = 1/fs # tamaño de paso con fs T = 1/f0 # periodo de señal dtc = Ts/fs_veces # suavizar x(t), sobremuestreo #https://blog.espol.edu.ec/telg1001/senales-escalon-e-impulso/ #u = lambda t: np.piecewise(t,t>=0,[1,0]) u = lambda t: np.heaviside(t,1) # pulso Sinc(t) # tambien definido como np.sinc() u1 = lambda t: u(t+Ts*pulso_ancho/2) u2 = lambda t: u(t-Ts*pulso_ancho/2) sinc_tl = lambda t: ((np.sin(np.pi*t/Ts)/(np.pi*t/Ts))*(u1(t) - u2(t))) def sinc_t(t): np.seterr(invalid='ignore') # t==0 division para cero resultado = sinc_tl(t) # en t=0, resultado es nan resultado = np.nan_to_num(resultado, nan=1) # cambia nan por 1 return (resultado) # x[n] interpolacion en Ts, a muestreo fs muestras_n = len(xki) t_pulsos = pulso_ti(muestras_n,fs,fs_veces, pulso_ancho,pulso_causal) # unpulso muestreo t_unpulso = pulso_ti(1,fs,fs_veces, pulso_ancho,pulso_causal) t_pulsoEval= t_unpulso if pulso_causal: t_pulsoEval = t_unpulso-Ts*pulso_ancho/2 unpulso = sinc_t(t_pulsoEval) muestras_pulso = len(t_unpulso) muestras_N = len(xki) mitad_pulso = int(muestras_pulso/2) pulsos_vacio = np.zeros(len(t_pulsos),dtype=float) xn_pulsos = np.copy(pulsos_vacio) xk_pulsos = [] for j in range(0,muestras_N,1): # x(t) pulsos k0 = int(j*fs_veces) kn = k0 + muestras_pulso pulsoj = np.copy(pulsos_vacio) pulsoj[k0:kn]= pulsoj[k0:kn] + unpulso*xki[j] xk_pulsos.append(pulsoj) xn_pulsos = xn_pulsos+pulsoj return(t_pulsos,xn_pulsos,t_unpulso,unpulso,xk_pulsos) xn_list = xn_actualiza(fs,fs_veces,xki, pulso_ancho,pulso_causal) [t_pulsos,x_pulsos,t_unpulso,unpulso,xk_pulsos] = xn_list # x[n] # SALIDA # SALIDA print('fs:',fs,'Hz ; Ts:',Ts,' s') print('pulso_causal:',pulso_causal) print('muestras_pulso:',len(t_unpulso)) print('t_unpulso:',t_unpulso) print('muestras_tiempo:',len(t_pulsos)) # GRAFICAS interactivas---------------------------- from matplotlib.widgets import Slider, Button, TextBox from matplotlib.collections import LineCollection import telg1034 as dsp colores = ["blue", "orange", "green", "red", "purple", "brown"] fig, [graf_t,graf_n] = plt.subplots(2,1) t_causal = 0 if pulso_causal: t_causal = Ts*pulso_ancho/2 # lineas de cada pulso muestras_n = len(tki) tabla = [] for j in range(0,muestras_n,1): pulsoj = np.concatenate(([t_pulsos-t_causal],[xk_pulsos[j]]),axis=0) pulsoj = np.transpose(pulsoj) tabla.append(pulsoj) print('tamañotabla',np.shape(tabla)) linea_pulsosk = LineCollection(tabla,color=colores, linestyles='dashed') linea_pulsosk.set_array(t_pulsos) graf_t.add_collection(linea_pulsosk) # x(t) grafico entorno graf_t.axhline(0,color='black') graf_t.set_xlabel('t') graf_t.grid() texto = titulo + ' ; f0='+str(f0) texto = texto +' ; fs='+str(fs) graf_t.set_title(texto) graf_t.set_xlim([t_pulsos[0]-t_causal,t_pulsos[-1]-t_causal]) # x(t) componentes linea_xt, = graf_t.plot(ti,xti,label='x(t)') puntos_xn = graf_t.stem(tki,xki,label='x[n]',linefmt = 'C1:') #linea_pulso, = graf_t.plot(t_unpulso-t_causal,unpulso, # label='pulso',linestyle='dashed',lw=2) graf_t.legend() # x[n] grafico entorno graf_n.axhline(0,color='black') graf_n.set_xlabel('t_n') graf_n.grid() # x[n] componentes linea_xt0, = graf_n.plot(ti_0,xti_0,linestyle='dotted', label='x(t)') puntos_xki = graf_n.stem(tkj,xki,linefmt = 'C1:') #, label='x[n]') linea_x_pulsos, = graf_n.plot(t_pulsos,x_pulsos,label='x(t) pulsos') graf_n.set_xlim([t_pulsos[0],t_pulsos[-1]]) graf_n.legend() plt.tight_layout() # plt.show() # grafica interactiva plt.subplots_adjust(bottom=0.25) # espacio widgets # slider: barras para valores # amplitud slider [x,y,ancho,alto] fs_donde = plt.axes([0.2, 0.10, 0.65, 0.03]) df_pasos = 5 fs_slider = Slider(fs_donde, 'fs', (f0//df_pasos)*df_pasos, (max([fs,10*f0])+2*df_pasos), valinit = fs, valstep = df_pasos, orientation='horizontal') def grafico_actualiza(val): # actualiza valores x,y fs = fs_slider.val Ts = 1/fs # tamaño de paso con fs t_causal = 0 if pulso_causal: t_causal = Ts*pulso_ancho/2 xt_list = xt_actualiza(xt,f0,fs,fs_veces,nT, pulso_ancho,pulso_causal) [ti,xti,tki,xki,tkj,ti_0,xti_0] = xt_list # x(t),x[n],x(t)_alias0 dsp.stem_update(puntos_xn,tki,xki,graf_t) # x[n] dsp.stem_update(puntos_xki,tkj,xki,graf_n) linea_xt0.set_xdata(ti_0) #x(t)_alias0 linea_xt0.set_ydata(xti_0) xn_list = xn_actualiza(fs,fs_veces,xki,pulso_ancho,pulso_causal) [t_pulsos,x_pulsos,t_unpulso,unpulso,xk_pulsos] = xn_list # x[n] pulsos, pulso linea_x_pulsos.set_xdata(t_pulsos) # x[n] pulsos linea_x_pulsos.set_ydata(x_pulsos) #linea_pulso.set_xdata(t_unpulso-t_causal) # pulso lti #linea_pulso.set_ydata(unpulso) # lineas de cada pulso muestras_n = len(tki) tabla = [] for j in range(0,muestras_n,1): pulsoj = np.concatenate(([t_pulsos-t_causal],[xk_pulsos[j]]),axis=0) pulsoj = np.transpose(pulsoj) tabla.append(pulsoj) linea_pulsosk.set_segments(tabla) texto = titulo+' ; f0='+str(f0) texto = texto +' ; fs='+str(fs) graf_t.set_title(texto) graf_t.set_xlim([t_pulsos[0]-t_causal,t_pulsos[-1]-t_causal]) graf_n.set_xlim([t_pulsos[0],t_pulsos[-1]]) fig.canvas.draw_idle() # actualiza figura # boton reinicio de gráfica btn_rstdonde = plt.axes([0.85, 0.025, 0.1, 0.04]) btn_rst = Button(btn_rstdonde, 'Reset', hovercolor='0.975') def grafico_reinicia(event): fs_slider.reset() return() # objetos interactivos fs_slider.on_changed(grafico_actualiza) btn_rst.on_clicked(grafico_reinicia) plt.show()
[ interpola Sinc ] [ ejemplo ] [ algoritmo ] [ gráfica interactiva ]