[ interpola triángulo ] [ ejemplo ] [ algoritmo ] [ gráfica interactiva ]
..
1. Interpolación Lineal
Referencia: McClellan 4-3.3 p143
La interpolación lineal, con pulso triangular, o polinomio de primer orden consiste en los segmentos de línea:
p(t) = \begin{cases} 1-\frac{|t|}{Ts} & -T_s \leq t \leq -\frac{1}{2} T_s \\ 0 & otro caso \end{cases}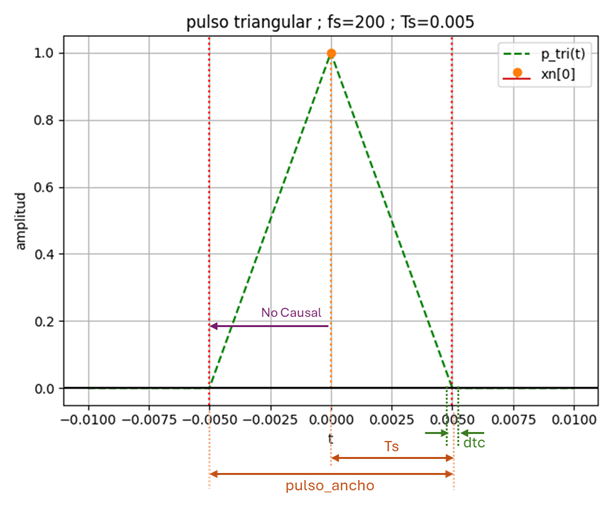
El ancho del pulso es de dos veces el periodo de muestreo Ts, lo que causa que los pulsos se superpongan entre muestras. El resultado de la interpolación de varios impulsos requiere que se sumen las partes superpuestas, situación a considerar en la variable tiempo t del resultado y que se resume en la función pulso_ti().
1.1 Algoritmo en Python para un pulso triangular
# D-to-C, Interpolacion con pulso triangular # ejemplo 4.3.3 p143 import numpy as np import matplotlib.pyplot as plt # INGRESO fs = 200 # Hz muestreo fs_veces = 10 # suavizar x(t), sobremuestreo titulo = 'pulso triangular' nT = 2.0 # graficar periodos de la señal # pulso triangular pulso_causal = True # No causal, pulso centrado en cero # PROCEDIMIENTO Ts = 1/fs # muestreo periodo #https://blog.espol.edu.ec/telg1001/senales-escalon-%ce%bct-e-impulso-%ce%b4t/ #u = lambda t: np.piecewise(t,t>=0,[1,0]) u = lambda t: np.heaviside(t,1) # pulso triangular u1 = lambda t: u(t+Ts) u2 = lambda t: u(t-Ts) triangular = lambda t: (1-abs(t)/Ts)*(u1(t) - u2(t)) pulso_ancho = 2 # x[n] interpolacion en Ts, a muestreo fs Ts = 1/fs ; dtc = Ts/fs_veces t_unpulso = np.arange(-Ts*nT,Ts*nT+dtc,dtc) unpulso = triangular(t_unpulso) # SALIDA print('muestras:',len(t_unpulso)) print('t_unpulso:',t_unpulso) # GRAFICA de un pulso # p(t) componentes plt.plot(t_unpulso,unpulso, color='green',linestyle='dashed', label='p_tri(t)') plt.axvline(-Ts,color='red',linestyle='dotted') plt.axvline(Ts,color='red',linestyle='dotted') plt.stem([0],[1],linefmt = 'C1:', label='xn[0]') plt.axhline(0,color='Black') # grafica entorno plt.xlabel('t') plt.ylabel('amplitud') texto = titulo + ' ; fs='+str(fs) texto = texto +' ; Ts='+str(1/fs) plt.title(texto) plt.grid() plt.legend() plt.tight_layout() plt.show()
[ interpola triángulo ] [ ejemplo ] [ algoritmo ] [ gráfica interactiva ]
..
2. Ejemplo con señal Senoidal y pulsos triangular
La señal x(t) tipo cosenoidal con f0=83 Hz y de amplitud unitaria, se convierte a muestras discretas con frecuencia fs=200 Hz.
x(t) = \cos(2\pi (83)t)
Cada pulso triangular aplicado en una muestra se superpone al siguiente aplicado en la muestra nTs.
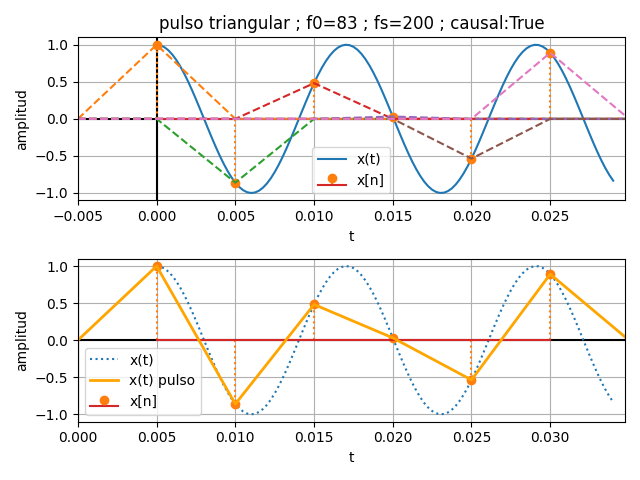En la reconstrucción para el vector tiempo t_pulsos, se debe considerar que el primer pulso empieza antes que el valor de la muestra, por lo que la señal presenta un retraso de mitad de pulso.
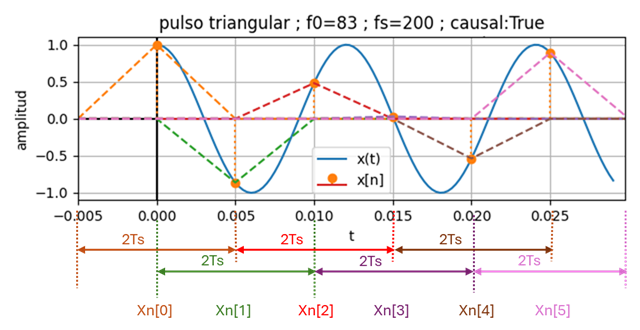En este caso, como el ancho del pulso es 2Ts, la señal resultante se atrasa Ts com se muestra en la gráfica.
La función pulso_ti() construye el vector de tiempo considerando ancho del pulso y el número de muestras x[n]. El inicio del vector tiempo también considera si el sistema es causal al aplicar el atraso a la unidad de tiempo, pues la reconstrucción empieza en el tiempo cero para las señales en tiempo real.
El vector tiempo también debe considerar la frecuencia de muestreo fs y para la gráfica el sobre-muestreo fs_veces. Al final se observa que la señal reconstruida tiene una duración adicional al tiempo de la última muestra, por lo que se añade una duración de mitad de pulso al extremo final. El efecto se observa en la señal x(t)_pulsos.
[ interpola triángulo ] [ ejemplo ] [ algoritmo ] [ gráfica interactiva ]
..
3.Algoritmo en Python Interpola con pulso triangular
En la reconstrucción de la señal x(t) usando pulsos, se realiza un proceso semejante al aplicado en pulso_ti() , en las partes que se superponen los impulsos se suman para dar un resultado de interpolación lineal de rectas que unen los valores de las muestras.
# D-to-C, Interpolacion con pulso triangular # ejemplo 4.3.3 p143 import numpy as np import matplotlib.pyplot as plt # INGRESO # señal x(t) f0 = 83 # frecuencia de senal fase0 = 0 # [0,2*np.pi] xt = lambda t: np.cos(2*np.pi*f0*t + fase0) fs = 200 # Hz muestreo fs_veces = 20 # suavizar x(t), sobremuestreo nT = 2.4 # graficar periodos de la señal titulo = 'pulso triangular' # pulso triangular pulso_causal = True # No causal, pulso centrado en cero pulso_ancho = 2 casicero = 1e-10 # cero para valores menores # PROCEDIMIENTO Ts = 1/fs # tamaño de paso con fs T = 1/f0 # periodo de señal dtc = Ts/fs_veces # suavizar x(t), sobremuestreo # muestreo x(t) ti = np.arange(0,nT*T+dtc,dtc) xti = xt(ti) ti_max = max(ti) # muestreo x[n] muestras_n = 2 if ti_max>=Ts: # varias muestras muestras_n = int(ti_max/Ts)+1 ki = np.arange(0,muestras_n,1,dtype=int) tki = ki*Ts # muestras x[n] xki = xt(tki) tkj = tki # x[n] alias0 ti_0 = ti # No Causal, pulso centrado en cero if pulso_causal: # Causal tkj = tki + Ts*pulso_ancho/2 ti_0 = ti + Ts*pulso_ancho/2 xti_0 = xti def pulso_ti(muestras_n,fs,fs_veces,ancho=1,causal=True): ''' tiempos para las n muestras x(t) con pulsos a frecuencia fs. Para suavizar el pulso se usa fs_veces para el sobremuestreo. El ancho del pulso es veces el periodo de muestreo (1/Ts) Si es causal el tiempo inicia en t=0, centrado en cero. Si no es causal el tiempo inicia t en mitad de intervalo. ''' Ts = 1/fs # muestreo periodo dtc = Ts/fs_veces # suavizar pulso(t), sobremuestreo t_Ts = np.arange(0,Ts,dtc) # tiempo en periodo Ts sobremuestreado mitad = Ts*ancho/2 t_mitad = np.arange(0,mitad,dtc) t_pulsos = np.copy(t_mitad) # mitad de primer pulso for i in range(1,muestras_n,1): t_pulsos = np.concatenate((t_pulsos,t_Ts + t_pulsos[-1]+dtc)) # mitad de último pulso para muestra_n t_pulsos = np.concatenate((t_pulsos,t_mitad + t_pulsos[-1]+dtc)) # https://blog.espol.edu.ec/telg1001/sistemas-causales-y-no-causales/ if causal == False: # centrado en cero t_pulsos = t_pulsos - mitad return(t_pulsos) # x[n] interpolacion en Ts, a muestreo fs t_pulsos = pulso_ti(muestras_n,fs,fs_veces, pulso_ancho,pulso_causal) #https://blog.espol.edu.ec/telg1001/senales-escalon-%ce%bct-e-impulso-%ce%b4t/ #u = lambda t: np.piecewise(t,t>=0,[1,0]) u = lambda t: np.heaviside(t,1) # pulso triangular u1 = lambda t: u(t+Ts*pulso_ancho/2) u2 = lambda t: u(t-Ts*pulso_ancho/2) triangular = lambda t: (1-abs(t)*fs)*(u1(t) - u2(t)) # unpulso muestreo t_unpulso = pulso_ti(1,fs,fs_veces, pulso_ancho,pulso_causal) t_pulsoEval= t_unpulso if pulso_causal: t_pulsoEval = t_unpulso-Ts*pulso_ancho/2 unpulso = triangular(t_pulsoEval) muestras_pulso = len(t_unpulso) muestras_N = len(xki) mitad_pulso = int(muestras_pulso/2) pulsos_vacio = np.zeros(len(t_pulsos),dtype=float) xn_pulsos = np.copy(pulsos_vacio) xk_pulsos = [] for j in range(0,muestras_N,1): # x(t) pulsos k0 = int(j*fs_veces) kn = k0 + muestras_pulso pulsoj = np.copy(pulsos_vacio) pulsoj[k0:kn]= pulsoj[k0:kn] + unpulso*xki[j] xk_pulsos.append(pulsoj) xn_pulsos = xn_pulsos+pulsoj # SALIDA print('muestras_pulso:',muestras_pulso) print('t_unpulso:',t_unpulso) print('muestras_tiempo:',len(t_pulsos)) # GRAFICAS ---------------------------- fig, [graf_t,graf_n] = plt.subplots(2,1) # x(t) grafico entorno t_causal = 0 if pulso_causal: t_causal = Ts*pulso_ancho/2 graf_t.axhline(0,color='black') graf_t.axvline(0,color='black') graf_t.set_xlabel('t') graf_t.set_ylabel('amplitud') graf_t.set_xlim([t_pulsos[0]-t_causal, t_pulsos[-1]-t_causal]) graf_t.grid() texto = titulo + ' ; f0='+str(f0) texto = texto + ' ; fs='+str(fs) texto = texto + ' ; causal:'+str(pulso_causal) graf_t.set_title(texto) # x(t) componentes graf_t.plot(ti,xti,label='x(t)') graf_t.stem(tki,xki,label='x[n]',linefmt = 'C1:') for i in range(0,muestras_N,1): graf_t.plot(t_pulsos-t_causal,xk_pulsos[i], linestyle='dashed') graf_t.legend() # x[n] grafico entorno graf_n.axhline(0,color='black') graf_n.axvline(0,color='black') graf_n.set_xlabel('t') graf_n.set_ylabel('amplitud') graf_n.set_xlim([t_pulsos[0],t_pulsos[-1]]) graf_n.grid() # x[n] componentes graf_n.plot(ti_0,xti_0,linestyle='dotted', label='x(t)') graf_n.stem(tkj,xki,label='x[n]',linefmt = 'C1:') graf_n.plot(t_pulsos,xn_pulsos, label='x(t) pulso', lw=2, color='orange') graf_n.legend() plt.tight_layout() plt.show()
[ interpola triángulo ] [ ejemplo ] [ algoritmo ] [ gráfica interactiva ]
..
4. Algoritmo en Python para gráfico interactivo con fs
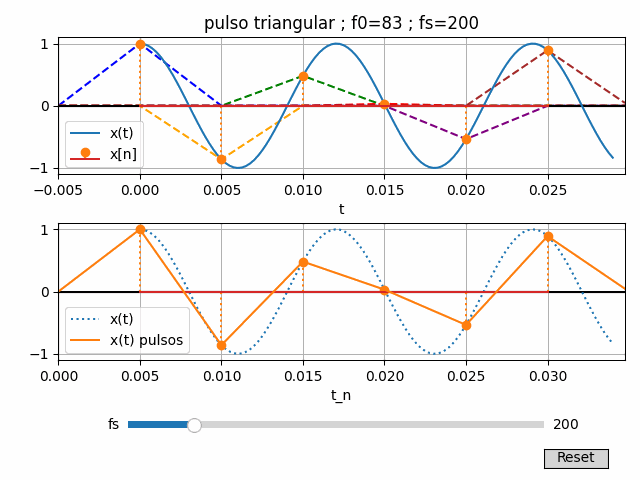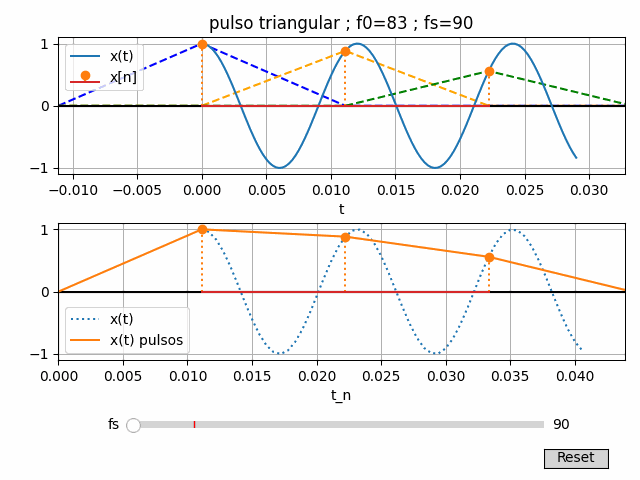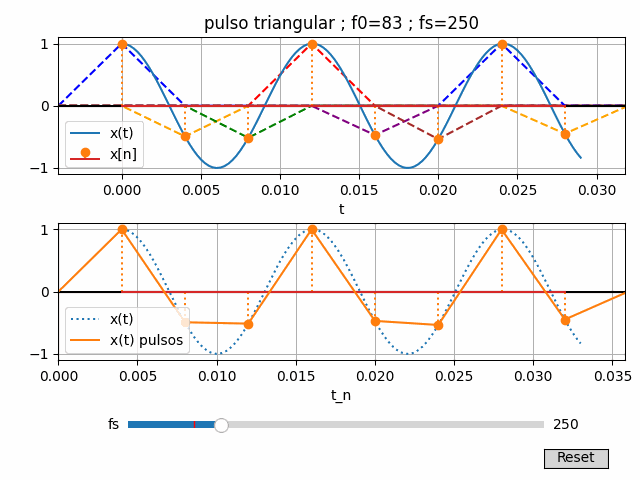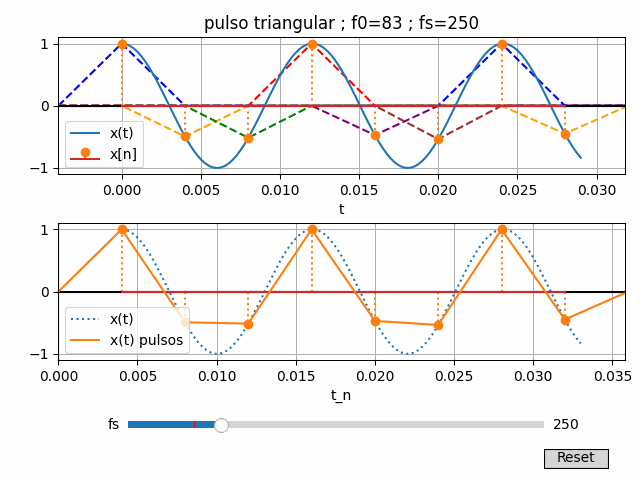Las instrucciones en Python son semejantes al caso con pulso rectangular.
Para dibujar cada pulso, se usa un objeto de líneas agrupadas o LineCollection() que permite actualizar las lineas al actualizar la tabla.
# D-to-C, Interpolacion con pulso triangular # grafico interactivo # ejemplo 4.3.3 p143 import numpy as np import matplotlib.pyplot as plt # INGRESO # señal x(t) f0 = 83 # frecuencia de senal fase0 = 0 # [0,2*np.pi] xt = lambda t: np.cos(2*np.pi*f0*t + fase0) fs = 200 # Hz muestreo fs_veces = 20 # suavizar x(t), sobremuestreo nT = 2.4 # graficar periodos de la señal titulo = 'pulso triangular' # pulso triangular pulso_causal = True # No causal, pulso centrado en cero pulso_ancho = 2 casicero = 1e-10 # cero para valores menores # PROCEDIMIENTO Ts = 1/fs # tamaño de paso con fs T = 1/f0 # periodo de señal dtc = Ts/fs_veces # suavizar x(t), sobremuestreo def xt_actualiza(xt,f0,fs,fs_veces,nT, pulso_ancho=1,pulso_causal=True): ''' x(t) muestreada a fs, para nT periodos de x(t). gráfica suavizada con fs_veces. No causal, pulso centrado en cero. Causal el pulso inicia en t=0. ''' Ts = 1/fs # tamaño de paso con fs T = 1/f0 # periodo de señal dtc = Ts/fs_veces # suavizar x(t), sobremuestreo # muestreo x(t) ti = np.arange(0,nT*T+dtc,dtc) xti = xt(ti) ti_max = max(ti) # muestreo x[n] muestras_n = 2 if ti_max>=Ts: # varias muestras muestras_n = int(ti_max/Ts)+1 ki = np.arange(0,muestras_n,1,dtype=int) tki = ki*Ts # muestras x[n] xki = xt(tki) tkj = tki # x[n] alias0 ti_0 = ti # No Causal, pulso centrado en cero if pulso_causal: # Causal tkj = tki + Ts*pulso_ancho/2 ti_0 = ti + Ts*pulso_ancho/2 xti_0 = xti return(ti,xti,tki,xki,tkj,ti_0,xti_0) xt_list = xt_actualiza(xt,f0,fs,fs_veces,nT, pulso_ancho,pulso_causal) [ti,xti,tki,xki,tkj,ti_0,xti_0] = xt_list # x(t),x[n],x(t)_alias0 muestras_n = len(tki) def pulso_ti(muestras_n,fs,fs_veces,ancho=1,causal=True): ''' tiempos para las n muestras x(t) con pulsos a frecuencia fs. Para suavizar el pulso se usa fs_veces para el sobremuestreo. El ancho del pulso es veces el periodo de muestreo (1/Ts) Si es causal el tiempo inicia en t=0, centrado en cero. Si no es causal el tiempo inicia t en mitad de intervalo. ''' Ts = 1/fs # muestreo periodo dtc = Ts/fs_veces # suavizar pulso(t), sobremuestreo t_Ts = np.arange(0,Ts,dtc) # tiempo en periodo Ts sobremuestreado mitad = Ts*ancho/2 t_mitad = np.arange(0,mitad,dtc) t_pulsos = np.copy(t_mitad) # mitad de primer pulso for i in range(1,muestras_n,1): t_pulsos = np.concatenate((t_pulsos,t_Ts + t_pulsos[-1]+dtc)) # mitad de último pulso para muestra_n t_pulsos = np.concatenate((t_pulsos,t_mitad + t_pulsos[-1]+dtc)) # https://blog.espol.edu.ec/telg1001/sistemas-causales-y-no-causales/ if causal == False: # centrado en cero t_pulsos = t_pulsos - mitad return(t_pulsos) def xn_actualiza(fs,fs_veces,xki, pulso_ancho=1,pulso_causal=True): Ts = 1/fs # tamaño de paso con fs T = 1/f0 # periodo de señal dtc = Ts/fs_veces # suavizar x(t), sobremuestreo #https://blog.espol.edu.ec/telg1001/senales-escalon-%ce%bct-e-impulso-%ce%b4t/ #u = lambda t: np.piecewise(t,t>=0,[1,0]) u = lambda t: np.heaviside(t,1) # pulso triangular u1 = lambda t: u(t+Ts*pulso_ancho/2) u2 = lambda t: u(t-Ts*pulso_ancho/2) triangular = lambda t: (1-abs(t)*fs)*(u1(t) - u2(t)) # x[n] interpolacion en Ts, a muestreo fs muestras_n = len(xki) t_pulsos = pulso_ti(muestras_n,fs,fs_veces, pulso_ancho,pulso_causal) # unpulso muestreo t_unpulso = pulso_ti(1,fs,fs_veces, pulso_ancho,pulso_causal) t_pulsoEval= t_unpulso if pulso_causal: t_pulsoEval = t_unpulso-Ts*pulso_ancho/2 unpulso = triangular(t_pulsoEval) muestras_pulso = len(t_unpulso) muestras_N = len(xki) mitad_pulso = int(muestras_pulso/2) pulsos_vacio = np.zeros(len(t_pulsos),dtype=float) xn_pulsos = np.copy(pulsos_vacio) xk_pulsos = [] for j in range(0,muestras_N,1): # x(t) pulsos k0 = int(j*fs_veces) kn = k0 + muestras_pulso pulsoj = np.copy(pulsos_vacio) pulsoj[k0:kn]= pulsoj[k0:kn] + unpulso*xki[j] xk_pulsos.append(pulsoj) xn_pulsos = xn_pulsos+pulsoj return(t_pulsos,xn_pulsos,t_unpulso,unpulso,xk_pulsos) xn_list = xn_actualiza(fs,fs_veces,xki, pulso_ancho,pulso_causal) [t_pulsos,x_pulsos,t_unpulso,unpulso,xk_pulsos] = xn_list # x[n] # SALIDA print('fs:',fs,'Hz ; Ts:',Ts,' s') print('pulso_causal:',pulso_causal) print('muestras_pulso:',len(t_unpulso)) print('t_unpulso:',t_unpulso) print('muestras_tiempo:',len(t_pulsos)) # GRAFICAS interactivas---------------------------- from matplotlib.widgets import Slider, Button, TextBox from matplotlib.collections import LineCollection import telg1034 as dsp colores = ["blue", "orange", "green", "red", "purple", "brown"] fig, [graf_t,graf_n] = plt.subplots(2,1) t_causal = 0 if pulso_causal: t_causal = Ts*pulso_ancho/2 # lineas de cada pulso muestras_n = len(tki) tabla = [] for j in range(0,muestras_n,1): pulsoj = np.concatenate(([t_pulsos-t_causal],[xk_pulsos[j]]),axis=0) pulsoj = np.transpose(pulsoj) tabla.append(pulsoj) print('tamañotabla',np.shape(tabla)) linea_pulsosk = LineCollection(tabla,color=colores, linestyles='dashed') linea_pulsosk.set_array(t_pulsos) graf_t.add_collection(linea_pulsosk) # x(t) grafico entorno graf_t.axhline(0,color='black') graf_t.set_xlabel('t') graf_t.grid() texto = titulo + ' ; f0='+str(f0) texto = texto +' ; fs='+str(fs) graf_t.set_title(texto) graf_t.set_xlim([t_pulsos[0]-t_causal,t_pulsos[-1]-t_causal]) # x(t) componentes linea_xt, = graf_t.plot(ti,xti,label='x(t)') puntos_xn = graf_t.stem(tki,xki,label='x[n]',linefmt = 'C1:') #linea_pulso, = graf_t.plot(t_unpulso-t_causal,unpulso, # label='pulso',linestyle='dashed',lw=2) graf_t.legend() # x[n] grafico entorno graf_n.axhline(0,color='black') graf_n.set_xlabel('t_n') graf_n.grid() # x[n] componentes linea_xt0, = graf_n.plot(ti_0,xti_0,linestyle='dotted', label='x(t)') puntos_xki = graf_n.stem(tkj,xki,linefmt = 'C1:') #, label='x[n]') linea_x_pulsos, = graf_n.plot(t_pulsos,x_pulsos,label='x(t) pulsos') graf_n.set_xlim([t_pulsos[0],t_pulsos[-1]]) graf_n.legend() plt.tight_layout() # plt.show() # grafica interactiva plt.subplots_adjust(bottom=0.25) # espacio widgets # slider: barras para valores # amplitud slider [x,y,ancho,alto] fs_donde = plt.axes([0.2, 0.10, 0.65, 0.03]) df_pasos = 5 fs_slider = Slider(fs_donde, 'fs', (f0//df_pasos)*df_pasos, (max([fs,10*f0])+2*df_pasos), valinit = fs, valstep = df_pasos, orientation='horizontal') def grafico_actualiza(val): # actualiza valores x,y fs = fs_slider.val Ts = 1/fs # tamaño de paso con fs t_causal = 0 if pulso_causal: t_causal = Ts*pulso_ancho/2 xt_list = xt_actualiza(xt,f0,fs,fs_veces,nT, pulso_ancho,pulso_causal) [ti,xti,tki,xki,tkj,ti_0,xti_0] = xt_list # x(t),x[n],x(t)_alias0 dsp.stem_update(puntos_xn,tki,xki,graf_t) # x[n] dsp.stem_update(puntos_xki,tkj,xki,graf_n) linea_xt0.set_xdata(ti_0) #x(t)_alias0 linea_xt0.set_ydata(xti_0) xn_list = xn_actualiza(fs,fs_veces,xki,pulso_ancho,pulso_causal) [t_pulsos,x_pulsos,t_unpulso,unpulso,xk_pulsos] = xn_list # x[n] pulsos, pulso linea_x_pulsos.set_xdata(t_pulsos) # x[n] pulsos linea_x_pulsos.set_ydata(x_pulsos) #linea_pulso.set_xdata(t_unpulso-t_causal) # pulso lti #linea_pulso.set_ydata(unpulso) # lineas de cada pulso muestras_n = len(tki) tabla = [] for j in range(0,muestras_n,1): pulsoj = np.concatenate(([t_pulsos-t_causal],[xk_pulsos[j]]),axis=0) pulsoj = np.transpose(pulsoj) tabla.append(pulsoj) linea_pulsosk.set_segments(tabla) texto = titulo+' ; f0='+str(f0) texto = texto +' ; fs='+str(fs) graf_t.set_title(texto) graf_t.set_xlim([t_pulsos[0]-t_causal,t_pulsos[-1]-t_causal]) graf_n.set_xlim([t_pulsos[0],t_pulsos[-1]]) fig.canvas.draw_idle() # actualiza figura # boton reinicio de gráfica btn_rstdonde = plt.axes([0.85, 0.025, 0.1, 0.04]) btn_rst = Button(btn_rstdonde, 'Reset', hovercolor='0.975') def grafico_reinicia(event): fs_slider.reset() return() # objetos interactivos fs_slider.on_changed(grafico_actualiza) btn_rst.on_clicked(grafico_reinicia) plt.show()
[ interpola triángulo ] [ ejemplo ] [ algoritmo ] [ gráfica interactiva ]