1ra Evaluación 2024-2025 PAO I. 2/Julio/2024
Tema 2 (40 puntos) La distribución de temperatura en estado estable en una placa cuadrada caliente está modelada por la ecuación de Laplace [1], cuya solución en su forma iterativa cuando el factor
(Δy)2/(Δx) = 1 se interpreta como:
“La temperatura en los nodos de la malla de una placa se puede calcular con el promedio de las temperaturas de los 4 nodos vecinos de la izquierda, derecha, arriba y abajo” [2].
Considere placa cuadrada de 4.5 cm de lado tiene la temperatura en los nodos de los bordes como se indica en la figura. 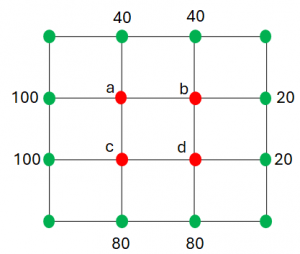
a) Plantee el sistema de ecuaciones para encontrar los valores en los nodos a, b, c, d. Use la solución descrita para la ecuación de Laplace.
b) Presente la matriz aumentada y Muestre los pasos detallados para el pivoteo parcial por filas.
c) Desarrolle las expresiones para resolver mediante el método de Gauss-Seidel. Considere para el vector inicial Xo, valores intermedios entre las temperaturas de los bordes de la placa.
d) Realice al menos 3 iteraciones, indicando el error por iteración.
e) Analice la convergencia del método, número de condición y resultados obtenidos.
Adjunte los archivos del algoritmo y resultados de computadora utilizados.
Rúbrica: Literal a (5 puntos), literal b (5 puntos), literal c (5 puntos), literal d (15 puntos). literal e (5 puntos) Adjuntos (5 puntos)
Referencia: [1] Ejercicio 12.39 p339 Steven C. Chapra. Numerical Methods 7th Edition.
[2] Ecuaciones Elípticas. Método iterativo. http://blog.espol.edu.ec/analisisnumerico/edp-elipticas-metodo-iterativo/
