1ra Evaluación I Término 2019-2020. 2/Julio/2019. MATG1013
Tema 2. ( 30 puntos) Considere los siguientes vectores: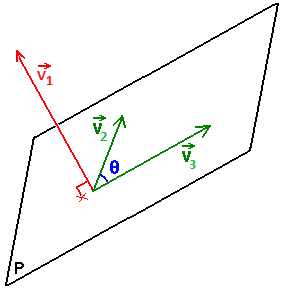
V1 = (2,-3,a)
V2=(b,1,-4)
V3= (3,c,2)
Se sabe que V1 es perpendicular a V2 y V3.
También se sabe que V2.V3=2.
Use un método para encontrar el valor de las incógnitas a,b,c
a) Plantee el sistema
b) Resuelva con el método de eliminación de Gauss
c) Vuelva a resolver con el método de Jacobi con x(0) = [0,0,0], realice tres iteraciones
d) Encuentre el residuo, cota del error absoluto y relativo
Rúbrica: literal a (5 puntos), literal b, ordenar las ecuaciones(5 puntos), método Gauss (10 puntos); literal c, aplicarJacobi (5 puntos), literal d (5 puntos)
Notas:
– Todos los temas deben mostrar evidencia del desarrollo del método numérico planteado.
– En geometría euclídea se tiene, dos vectores v1 y v2 que son ortogonales forman un ángulo recto, por lo tanto v1 ⋅ v2 = 0. https://es.wikipedia.org/wiki/Ortogonalidad_(matem%C3%A1ticas)
Referencia: Chapra 5ed. problema 10.18 p304, pdf 328.
