2da Evaluación 2022-2023 PAO I. 30/Agosto/2022
Tema 2. (30 puntos) El circuito de la figura 2a tiene el interruptor en posición cerrada por largo tiempo antes de t=0, con lo que la corriente en el inductor será de 2 Amperios, y(0)=2. Para t<0, el inductor opera como un conductor sin caída de voltaje, el capacitor está cargado a 10V y solo pasaría corriente por la resistencia de 5 Ohm.
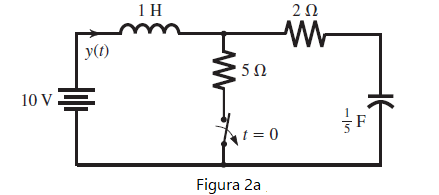
En el tiempo t=0, el interruptor se abre de forma instantánea y el circuito cambia al modelo de la figura 2b.
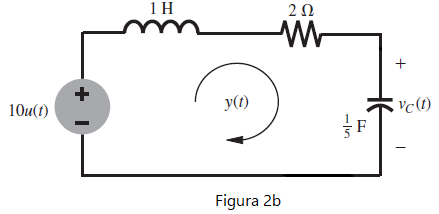
La corriente del inductor y(t) para t≥0 está dada por la ecuación:
En t=0, luego de abrir el interruptor, los voltajes de la fuente y el capacitor son iguales. La corriente inicial sobre el resistor de 2 A genera un voltaje que se compensa con el voltaje del inductor pero en signo opuesto. Lo que implica que y’(0) = -4
V_{Inductor} = - V_{resistor} y'(0) = -4Derive la expresión de corrientes y(t) para obtener una ecuación diferencial ordinaria.
a) Realice el planteamiento del problema usando el método de Runge-Kutta de 2do orden para 2da derivada
b) Desarrolle las expresiones para al menos tres iteraciones usando h=0.01
c) Estime el valor del error.
d) Muestre el resultado con el algoritmo para el intervalo t entre [0,5] segundos
Rúbrica: literal a (5 puntos), literal b (15 puntos), literal c (5 puntos), literal d (5 puntos)
Referencia: Lathi B.P. Green R. Linear Systems and Signals, 3rd Edition. ejemplo 4.13 p364