2da Evaluación 2022-2023 PAO I. 30/Agosto/2022
Tema 3. (40 puntos) Use el método de diferencias progresivas para aproximar la solución de la siguiente ecuación diferencial parcial parabólica:
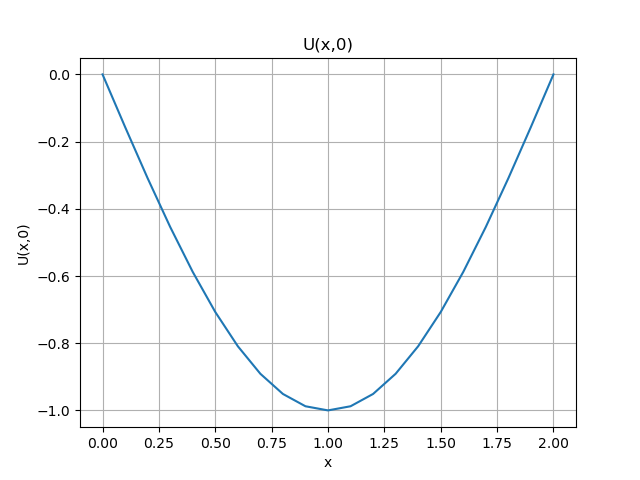
\frac{\partial U}{\partial t} - \frac{1}{9} \frac{\partial ^2 U}{\partial x^2} = 0 0 \leq x \leq 2, t>0Con las condiciones iniciales de borde e iniciales:
U(0,t) = U(2,t) = 0, t>0 U(x,0) = \cos \Big( \frac{\pi}{2}(x-3)\Big) , 0 \leq x \leq 2Aplique un método numérico para encontrar los valores de U(x,t) usando Δx = 1/3, Δt = 0.02 y muestre:
a. La grafica de malla
b. Ecuaciones de diferencias divididas a usar
c. Encuentre las ecuaciones considerando las condiciones dadas en el problema.
d. Determine el valor de λ, agrupando las constantes durante el desarrollo, revise la convergencia del método.
e. Resuelva para tres pasos
f. Estime el error (solo plantear)
g. Usando el algoritmo, aproxime la solución para t=0.02 y t=0.1
Rúbrica: literal a (3 puntos), literal b (2 puntos), literal c (5 puntos), literal d (5 puntos), aplicación de condiciones iniciales (5 puntos), literal e (10 puntos), literal f (5 puntos). literal g, usando algoritmo (5 puntos)
Referencia: 2Eva_IT2017_T3 EDP parabólica http://blog.espol.edu.ec/analisisnumerico/2eva_it2017_t3-edp-parabolica/
