2da Evaluación 2023-2024 PAO I. 29/Agosto/2023
Tema 2 (35 puntos) Una mejor aproximación a un péndulo oscilante con un ángulo θ más amplio y con un coeficiente de amortiguamiento μ se expresa con una ecuación diferencial ordinaria de segundo orden.
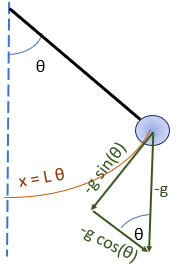\frac{d^2 \theta}{dt^2} = -\mu \frac{d\theta}{ dt}-\frac{g}{L}\sin (\theta)
g = 9.81 m/s2
L = 2 m
θ(0) = π/4 rad
θ’ (0) = 0 rad/s
El péndulo se suelta desde el reposo, desde un ángulo de π/4 respecto al eje vertical. El coeficiente de amortiguamiento μ=0.5 es proporcional a la velocidad angular.
a. Realice el planteamiento del ejercicio usando Runge-Kutta de 2do Orden
b. Desarrolle tres iteraciones para θ(t) con tamaño de paso h=0.2
c. Usando el algoritmo, aproxime la solución entre t=0 a t=10 s, adjunte sus resultados en la evaluación.
d. Realice una observación sobre el movimiento estimado del péndulo a lo largo del tiempo.
Rúbrica: literal a (5 puntos), literal b (15 puntos), literal c (10 puntos), literal d (5 puntos)
Referencia: 2Eva_IT2019_T2 Péndulo vertical
Vista general de ecuaciones diferenciales I Capítulo 1, 6min 54s. 3Blue1Brown 31-Marzo-2023.