3Eva_2021PAOI_T1 Tensiones en cables por carga variable

3ra Evaluación 2021-2022 PAO I. 14/Septiembre/2021

Tema 1 (20 puntos) Una carga P está sostenida por dos cables como se muestra en la figura.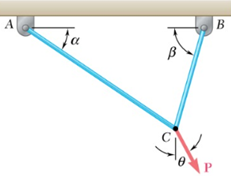

Las ecuaciones de equilibrio del sistema corresponden a:

\sum^n{F_x = 0} -T_{CA} \cos (\alpha) + T_{CB} \cos (\beta) + P \sin (\theta) = 0 \sum^n{F_y = 0} T_{CA} \sin (\alpha) + T_{CB} \sin (\beta) - P \cos (\theta) = 0

Se requiere determinar la tensión en cada cable para cualquiera de los valores de P y θ que se encuentran desde θ₁=β-90° hasta θ₂=90°- α , con incrementos dados Δθ.

Usando un algoritmo numérico con método directo para solución de un sistema de ecuaciones, determine para los siguientes conjuntos de  números: La tensión en cada cable para los valores de θ  que van de θ₁ a θ₂.

α = 35°, β = 75°, P = 400 lb, Δθ = 5°
α = 50°, β = 30°, P = 600 lb, Δθ = 5°
α = 40°, β = 60°, P = 2500 lb, Δθ = 5°

Nota: Observe que los valores de ángulos están presentados en grados sexagesimales

Referencia: Ferdinand P. Beer, E. Johnston, E. Eisenberg. 9va Ed. Cap2. Ejercicio 2.C4 Mecánica vectorial para ingenieros – Estática

Rúbrica: Planteamiento del problema (5 puntos), desarrollo del método directo (10 puntos), algoritmo (5 puntos)