3ra Evaluación 2021-2022 PAO I. 14/Septiembre/2021
Tema 2 (30 puntos) Para un circuito eléctrico mostrado en la figura, conocido también como un sistema LTIC (lineal contínuo invariante en el tiempo), la “respuesta a entrada cero” corresponde al comportamiento de la corriente y(t) cuando no se aplica una señal de entrada x(t) = 0.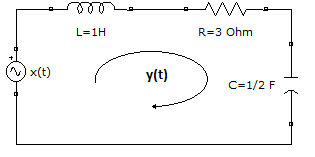 
La expresión que describe la relación de entrada x(t) y salida y(t) que permite analizar el sistema en un intervalo de tiempo es:
\frac{\delta^2 y(t)}{\delta t^2}+3 \frac{\delta y(t)}{ \delta t}+2 y(t) = \frac{\delta x(t)}{\delta t} =0Los componentes inductores y capacitores almacenan energía representada como condiciones iniciales y0(t) =0 , y’0(t) =-5
Considere como de interés el intervalo de tiempo entre [0,6] con al menos 60 tramos.
a) Realice el planteamiento para encontrar y(t) con las condiciones dadas, usando el método de Runge-Kutta de 2do orden
b) Desarrolle tres iteraciones con expresiones y valores, mostrando el uso del método anterior.
Referencia: Lathi B.P and Green R.A.(2018). Capítulo 2.1 p151.Linear Systems and Signals Third Edition. Oxford University Press.
http://blog.espol.edu.ec/telg1001/ltic-respuesta-entrada-cero-con-python/
Rúbrica: Planteo de ejercicio para el método requerido (5 puntos), tamaño de paso (5 puntos), iteraciones completas (15 puntos), desarrollo algorítmico, gráfica (5 puntos)