3ra Evaluación I Término 2018-2019. 11/Septiembre/2018. MATG1013
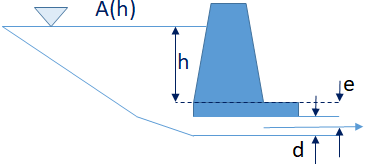
Tema 2. (40 puntos) Un estanque se drena a través de un tubo como se observa en la figura.
Con suposiciones simplificadoras, la ecuación diferencial siguiente describe cómo cambia la profundidad con el tiempo:
\frac{dh}{dt} = -\frac{\pi d^2}{4A(h)}\sqrt{2g(h+e)}
Donde:
h = profundidad (m),
t = tiempo (s),
d = diámetro del tubo (m),
A(h) = área de la superficie del estanque como función de la profundidad (m2),
g = constante gravitacional (9,81 m/s2) y
e es la profundidad de salida del tubo por debajo del fondo del estanque (m).
Con base en la tabla siguiente de área-profundidad, resuelva esta ecuación diferencial para determinar cuánto tiempo tomaría que el estanque se vacie, dado que h(0) = 6 m, d = 0.25 m, e = 0.3 m.
| h | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|
| A(h) | 1.17 | 0.97 | 0.67 | 0.45 | 0.32 | 0.18 | 0.02 |
a) Con las profundidades 0, 2, 4, 6, encuentre un modelo de trazador cúbico natural para modelar el área A(h) y calcule el error en h = 5 m
b) Use el método de Taylor de segundo orden con dt=1 s para aproximar el tiempo en que la profundidad es 3 m.
Rúbrica: literal a (20 puntos), literal b (20 puntos)
hi = np.array([6, 5, 4, 3, 2, 1, 0]) Ai = np.array([1.17, 0.97, 0.67, 0.45, 0.32, 0.18, 0.02])
Referencia: Chapra Ejercicio 28.24 p849, pdf873
Video: La ambiciosa Represa Hoover – INEXPLICABLE. History Latinoamérica.