[ Trazador Cúbico ] [ Algoritmo ] [ gráfica ] [ función ]
..
1. Trazador Cúbico - Planteamiento
Referencia: Burden 3.5 p105, Chapra 18.6.3 p532, Rodríguez 6.11.1 p244
Tiene como objetivo incorporar condiciones adicionales para la función en los extremos del intervalo donde se encuentran los puntos o "nodos".
Por ejemplo, si los datos son los de una trayectoria en un experimento de física, se podría disponer de la aceleración el punto inicial de las muestras (izquierda) y de salida (derecha) del intervalo de las muestras.
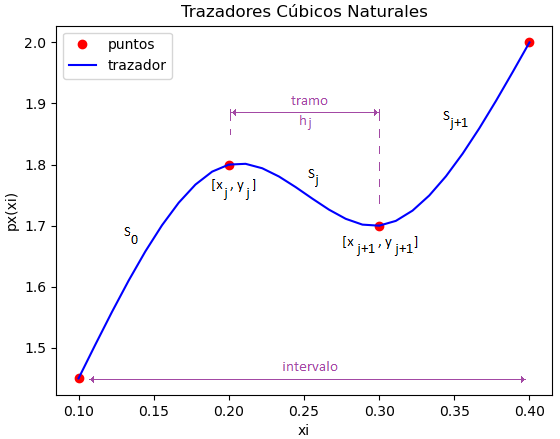
El método busca obtener un polinomio de tercer grado para cada sub-intervalo o tramo entre "nodos" consecutivos (j, j+1), de la forma:
S_j(x_j) = a_j + b_j (x-x_j) + c_j(x-xj)^2 + d_j(x-x_j)^3para cada j = 0, 1, ..., n-1
Para n datos existen n-1 tramos, cuatro incógnitas (coeficientes) que evaluar por cada tramo, como resultado 4(n-1) incógnitas para todo el intervalo .
Para los términos (xj+1- xj) de los tramos que se usan varias veces en el desarrollo, se simplifican como hj:
h_j = x_{j+1} - x_{j} S_j(x_j) = a_j + b_j h_j + c_j h_j^2 + d_jh_j^3Para generar el sistema de ecuaciones, se siguen los siguientes criterios:
1. Los valores de la función deben ser iguales en los nodos interiores
S_j(x_{j+1}) = f(x_{j+1}) = S_{j+1}(x_{j+1})2. Las primeras derivadas en los nodos interiores deben ser iguales
S'_j(x_{j+1}) = S'_{j+1}(x_{j+1})3. Las segundas derivadas en los nodos interiores deben ser iguales
S''_j(x_{j+1}) = S''_{j+1}(x_{j+1})4. El primer y último polinomio deben pasar a través de los puntos extremos
f(x_0) = S_0(x_0) = a_0 f(x_n) = S_n(x_n) = a_n5. Una de las condiciones de frontera se satisface:
5a. frontera libre o natural: Las segundas derivadas en los nodos extremos son cero
S''(x_0) = S''(x_n) = 0
5b. frontera sujeta: las primeras derivadas en los nodos extremos son conocidas
S'(x_0) = f'(x_0)
S'(x_n) = f'(x_n)
Tarea: Revisar en los libros. textos el planteamiento de las ecuaciones para resolver el sistema que se genera al plantear el polinomio.
Ubicar en el texto las ecuaciones resultantes, que son las que se aplicarán en el algoritmo.
[ Trazador Cúbico ] [ Algoritmo ] [ gráfica ] [ función ]
2. Algoritmo en Python
El algoritmo parte de lo desarrollado para "trazadores lineales", donde se presentaron los bloques para:
- construir el trazador en una tabla de polinomios por tramos
- realizar la gráfica con los trazadores en cada tramo
- evaluar cada uno de ellos en cada tramo con muestras suficientes para presentar una buena resolución o precisión en la gráfica
Del algoritmo básico se modifica entonces el bloque del cálculo de los polinomios de acuerdo al planteamiento de formulas y procedimientos para trazadores cúbicos naturales (enviado a revisar como tarea).
# Trazador cubico natural import numpy as np import sympy as sym def traza3natural(xi,yi, vertabla=False): ''' trazador cubico natural, 2da derivadas en los nodos extremos son cero ''' # Vectores como arreglo, numeros reales xi = np.array(xi,dtype=float) yi = np.array(yi,dtype=float) n = len(xi) h = np.diff(xi,n=1) # h tamano de paso # Sistema de ecuaciones A = np.zeros(shape=(n-2,n-2), dtype=float) B = np.zeros(n-2, dtype=float) S = np.zeros(n, dtype=float) A[0,0] = 2*(h[0]+h[1]) A[0,1] = h[1] B[0] = 6*((yi[2]-yi[1])/h[1] - (yi[1]-yi[0])/h[0]) for i in range(1,n-3,1): A[i,i-1] = h[i] A[i,i] = 2*(h[i]+h[i+1]) A[i,i+1] = h[i+1] B[i] = 6*((yi[i+2]-yi[i+1])/h[i+1] - (yi[i+1]-yi[i])/h[i]) A[n-3,n-4] = h[n-3] A[n-3,n-3] = 2*(h[n-3]+h[n-2]) B[n-3] = 6*((yi[n-1]-yi[n-2])/h[n-2] - (yi[n-2]-yi[n-3])/h[n-3]) # Resolver sistema de ecuaciones, S r = np.linalg.solve(A,B) #S[0] = 0; S[n-1] = 0 # Definidos en cero S[1:n-1] = r[0:n-2] # Coeficientes a = np.zeros(n-1, dtype = float) b = np.zeros(n-1, dtype = float) c = np.zeros(n-1, dtype = float) d = np.zeros(n-1, dtype = float) for j in range(0,n-1,1): a[j] = (S[j+1]-S[j])/(6*h[j]) b[j] = S[j]/2 c[j] = (yi[j+1]-yi[j])/h[j] - (2*h[j]*S[j]+h[j]*S[j+1])/6 d[j] = yi[j] # Polinomio trazador x = sym.Symbol('x') px_tabla = [] for j in range(0,n-1,1): pxtramo = a[j]*(x-xi[j])**3 + b[j]*(x-xi[j])**2 + c[j]*(x-xi[j])+ d[j] px_tabla.append(pxtramo) if vertabla==True: print('h:',h) print('A:') ; print(A) print('B:',B) ; print('S:',S) print('r:',r) print('coeficientes[ ,tramo]:') print('a:',a) ; print('b:',b) print('c:',c) ; print('d:',d) return(px_tabla) # PROGRAMA --------------- # INGRESO xi = [0.1 , 0.2, 0.3, 0.4] fi = [1.45, 1.8, 1.7, 2.0] titulo = 'Trazador cúbico natural o libre' # natural, 2da derivadas en los nodos extremos son cero # PROCEDIMIENTO n = len(xi) # Obtiene los polinomios por tramos px_tabla = traza3natural(xi,fi,vertabla=True) # SALIDA print(titulo) print('Polinomios por tramos: ') for i in range(0,n-1,1): print('x = [',xi[i],',',xi[i+1],']') print('expresion:',px_tabla[i]) print('simplificado:') sym.pprint(px_tabla[i].expand())
con lo que se obtiene el resultado por cada tramo
h: [0.1 0.1 0.1]
A:
[[0.4 0.1]
[0.1 0.4]]
B: [-27. 24.]
r: [-88. 82.]
S: [ 0. -88. 82. 0.]
coeficientes[ ,tramo]:
a: [-146.66666667 283.33333333 -136.66666667]
b: [ 0. -44. 41.]
c: [4.96666667 0.56666667 0.26666667]
d: [1.45 1.8 1.7 ]
Trazador cúbico natural o libre
Polinomios por tramos:
x = [ 0.1 , 0.2 ]
expresion: 4.96666666666667*x - 146.666666666667*(x - 0.1)**3 + 0.953333333333333
simplificado:
3 2
- 146.666666666667⋅x + 44.0⋅x + 0.566666666666666⋅x + 1.1
x = [ 0.2 , 0.3 ]
expresion: 0.566666666666666*x + 283.333333333333*(x - 0.2)**3 - 44.0*(x - 0.2)**2 + 1.68666666666667
simplificado:
3 2
283.333333333333⋅x - 214.0⋅x + 52.1666666666667⋅x - 2.34
x = [ 0.3 , 0.4 ]
expresion: 0.266666666666665*x - 136.666666666667*(x - 0.3)**3 + 41.0*(x - 0.3)**2 + 1.62
simplificado:
3 2
- 136.666666666667⋅x + 164.0⋅x - 61.2333333333333⋅x + 9.0
>>>
[ Trazador Cúbico ] [ Algoritmo ] [ gráfica ] [ función ]
..
3. Gráfica con Python
Para el trazado de la gráfica se añade al final del algoritmo:
# GRAFICA -------------- import matplotlib.pyplot as plt muestras = 10 # entre cada par de puntos # Puntos para grafica en cada tramo xtraza = np.array([],dtype=float) ytraza = np.array([],dtype=float) i = 0 while i<n-1: # cada tramo xtramo = np.linspace(xi[i],xi[i+1],muestras) # evalua polinomio del tramo pxk = sym.lambdify('x',px_tabla[i]) ytramo = pxk(xtramo) # vectores de trazador en x,y xtraza = np.concatenate((xtraza,xtramo)) ytraza = np.concatenate((ytraza,ytramo)) i = i + 1 # Graficar plt.plot(xtraza,ytraza, label='trazador') plt.plot(xi,fi,'o', label='puntos') plt.title(titulo) plt.xlabel('xi') plt.ylabel('px(xi)') plt.legend() plt.show()
[ Trazador Cúbico ] [ Algoritmo ] [ gráfica ] [ función ]
..
4. Trazador cúbico natural como función en Scipy
La librería Scipy dispone de una función para calcular los coeficientes de los trazadores cúbicos. Para el ejemplo del ejercicio se realiza el cálculo y los polinomios.
Trazador cúbico natural o libre
coeficientes:
a: [-146.66666667 283.33333333 -136.66666667]
b: [ 8.8817842e-15 -4.4000000e+01 4.1000000e+01]
c: [4.96666667 0.56666667 0.26666667]
d: [1.45 1.8 1.7 ]
Polinomios por tramos:
x = [ 0.1 , 0.2 ]
expresión: 4.96666666666667*x - 146.666666666667*(x - 0.1)**3 + 8.88178419700125e-15*(x - 0.1)**2 + 0.953333333333333
simplifica:
3 2
- 146.666666666667⋅x + 44.0⋅x + 0.566666666666662⋅x + 1.1
x = [ 0.2 , 0.3 ]
expresión: 0.566666666666667*x + 283.333333333333*(x - 0.2)**3 - 44.0*(x - 0.2)**2 + 1.68666666666667
simplifica:
3 2
283.333333333333⋅x - 214.0⋅x + 52.1666666666667⋅x - 2.34
x = [ 0.3 , 0.4 ]
expresión: 0.266666666666665*x - 136.666666666667*(x - 0.3)**3 + 41.0*(x - 0.3)**2 + 1.62
simplifica:
3 2
- 136.666666666667⋅x + 164.0⋅x - 61.2333333333333⋅x + 9.0
Las instrucciones en Python con la librería Scipy para trazadores cúbicos natural son:
# Trazador cúbico natural o libre con Scipy import numpy as np import scipy as sp import sympy as sym # INGRESO xi = [0.1 , 0.2, 0.3, 0.4] fi = [1.45, 1.8, 1.7, 2.0] # natural, 2da derivadas en los nodos extremos son cero cs_tipo = ((2, 0.0), (2, 0.0)) # natural # PROCEDIMIENTO # Vectores como arreglo, numeros reales xi = np.array(xi,dtype=float) fi = np.array(fi,dtype=float) n = len(xi) # coeficientes de trazadores cúbicos traza_cub = sp.interpolate.CubicSpline(xi,fi,bc_type=cs_tipo ) traza_coef = traza_cub.c # coeficientes a = traza_coef[0] b = traza_coef[1] c = traza_coef[2] d = traza_coef[3] # Polinomio trazador x = sym.Symbol('x') px_tabla = [] for j in range(0,n-1,1): pxtramo = a[j]*(x-xi[j])**3 + b[j]*(x-xi[j])**2 + c[j]*(x-xi[j])+ d[j] px_tabla.append(pxtramo) # SALIDA print('coeficientes:') print('a:',a) print('b:',b) print('c:',c) print('d:',d) print('Polinomios por tramos: ') for i in range(0,n-1,1): print('x = [',xi[i],',',xi[i+1],']') print('expresion:',px_tabla[i]) print('simplifica:') sym.pprint(px_tabla[i].expand())
la gráfica se puede generar con el bloque anterior
[ Trazador Cúbico ] [ Algoritmo ] [ gráfica ] [ función ]
Si los polinomios no se igualan entre los nodos, tampoco sus velocidades y aceleraciones; los puntos de inflexión en los nodos podrían generar una experiencia semejante a variaciones de velocidad y aceleración en una trayectoria como la mostrada en los siguientes videos.
youtube: slingshot ride
Car sales woman scares customers. maxman.tv. 4 enero 2016
[ Trazador Cúbico ] [ Algoritmo ] [ gráfica ] [ función ]