[ Cuadratura de Gauss ] [ Ejercicio ] [Algoritmo/función Python]

Cuadratura de Gauss

Referencia: Chapra 22.3 p655, Rodríguez 7.3 p294, Burden 4.7 p168

La cuadratura de Gauss aproxima el integral de una función en un intervalo [a,b] centrado en cero mediante un cálculo numérico con menos operaciones y evaluaciones de la función. Se representa como una suma ponderada:

I \cong \Big( \frac{b-a}{2} \Big)\Big(c_0f(x_a) + c_1f(x_b)\Big)

para la fórmula de dos puntos con referencia a una función centrada en cero y ancho unitario a cada lado, se tiene:

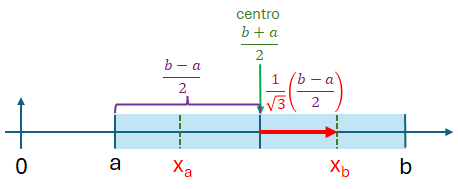
c_0 = c_1 = 1, x_0 = -\frac{1}{\sqrt{3}}, x_1 = \frac{1}{\sqrt{3}}

Para un intervalo de evaluación desplazado en el eje x se requiere convertir los puntos al nuevo intervalo. Se desplaza el punto cero al centro del intervalo [a,b] y se corrige el desplazamiento hacia la izquierda y derecha del centro con x₀ y x₁.

x_a = \frac{b+a}{2} - \frac{b-a}{2}\Big(\frac{1}{\sqrt{3}} \Big)

x_b = \frac{b+a}{2} + \frac{b-a}{2}\Big(\frac{1}{\sqrt{3}} \Big)

con lo que el resultado aproximado del integral se convierte en:

I \cong \frac{b-a}{2}(f(x_a) + f(x_b))

cuya fórmula es semejante a una mejor aproximación de un trapecio, cuyos promedios de alturas son puntos internos de [a,b], concepto mostrado en la gráfica.

[ Cuadratura de Gauss ] [ Ejercicio ] [Algoritmo/función Python]

Ejercicio

Para el ejercicio y comparación de resultado con los otros métodos, se realiza el cálculo para un tramo en el intervalo [a,b].

\int_1^3 \sqrt{x} \sin(x) dx

x_a = \frac{3+1}{2} + \frac{3-1}{2}\Big(\frac{1}{\sqrt{3}}\Big)= 1.4226

x_b = \frac{3+1}{2} + \frac{3-1}{2}\Big(\frac{1}{\sqrt{3}} \Big) = 2.5773

f(1.4226) = \sqrt{1.4226} \sin(1.4226) = 1.1796

f(2.5773) = \sqrt{2.5773} \sin(2.5773) = 0.8585

con lo que el resultado aproximado del integral se convierte en:

I \cong \frac{3-1}{2}(1.1796 + 0.8585) = 2.0382

que usando instrucciones de Python para obtener los valores:

>>> import numpy as np
>>> (3+1)/2-(3-1)/2*(1/np.sqrt(3))
1.4226497308103743
>>> (3+1)/2+(3-1)/2*(1/np.sqrt(3))
2.5773502691896257
>>> fx = lambda x: np.sqrt(x)*np.sin(x)
>>> fx(1.4226)
1.1796544827404145
>>> fx(2.5773)
0.8585957175067221
>>> ((3-1)/2)*(fx(1.4226)+fx(2.5773))
2.0382

el resultado se puede mejorar aumentando el número de tramos en el intervalo [a,b]. Por ejemplo, el resultado usando 4 tramos el resultado es semejante al usar el método del trapecio con 128 tramos, lo que muestra el ahorro en cálculos entre los métodos

Integral:  2.05357719003
>>>

Concepto:

Ejercicio:

[ Cuadratura de Gauss ] [ Ejercicio ] [Algoritmo/función Python]

Algoritmo con Python

Para el ejercicio anterior, usando al 4 segmentos y en cada uno aplicando Cuadratura de Gauss, el integral resultante es:

[xa,xb,f(xa),f(xb)]
[1.1056624327025935, 1.3943375672974065, 0.9397945621004238, 1.1624843542124732]
[xa,xb,f(xa),f(xb)]
[1.6056624327025935, 1.8943375672974065, 1.2663772374235445, 1.3049381813350678]
[xa,xb,f(xa),f(xb)]
[2.1056624327025935, 2.3943375672974065, 1.2484263248036183, 1.0516320347815513]
[xa,xb,f(xa),f(xb)]
[2.6056624327025935, 2.8943375672974065, 0.8242800855599416, 0.4163759798980186]
Integral:  2.0535771900286597

Instrucciones en Python usando la Cuadratura de Gauss de dos puntos para una función f(x):

# Integración: Cuadratura de Gauss de dos puntos
# modelo con varios tramos entre [a,b]
import numpy as np
import matplotlib.pyplot as plt

# cuadratura de Gauss de dos puntos
def integraCuadGauss2p(fx,a,b, vertabla=False):
    ''' funcion fx, intervalo[a,b]
        vertabla=True para ver resultados parciales 
    '''
    x0 = -1/np.sqrt(3)
    x1 = -x0
    xa = (b+a)/2 + (b-a)/2*(x0)
    xb = (b+a)/2 + (b-a)/2*(x1)
    area = ((b-a)/2)*(fx(xa) + fx(xb))
    if vertabla==True:
        print('[xa,xb,f(xa),f(xb)]')
        print([xa,xb,fx(xa),fx(xb)])
    return(area)

# INGRESO
fx = lambda x: np.sqrt(x)*np.sin(x)

# intervalo de integración
a = 1
b = 3
tramos = 4

# PROCEDIMIENTO
muestras = tramos+1
xi = np.linspace(a,b,muestras)
area = 0
for i in range(0,muestras-1,1):
    deltaA = integraCuadGauss2p(fx,xi[i],xi[i+1],vertabla=True)
    area = area + deltaA
# SALIDA
print('Integral: ', area)

Gráfica por tramos

La gráfica que complementa el resultado anterior, se realiza añadiendo las instrucciones presentadas a continuación.

Considere que la gráfica es útil con pocos tramos en el intervalo[a,b]

# GRAFICAR por cada Segmento/tramo
# para concepto con 'pocos' segmentos
subtramo = xi
muestrastramo = 10
x0 = -1/np.sqrt(3) 
x1 = 1/np.sqrt(3)

# gráficas de todos los tramos
aj = [] ; bj = []
xj = [] ; fj = []
recta = []

for i in range(0,tramos,1):
    ai = subtramo[i]
    bi = subtramo[i+1]
    
    xk = np.linspace(ai,bi,muestrastramo)
    fk = fx(xk)
    
    xj = xj + list(xk)
    fj = fj + list(fk)

    # puntos xa y xb por tramo
    xa = (bi+ai)/2 + (bi-ai)/2*(x0)
    xb = (bi+ai)/2 + (bi-ai)/2*(x1)
    
    aj.append(xa)
    bj.append(xb)
    
    # Recta entre puntos x0 y x1 por tramo
    m = (fx(xb)-fx(xa))/(xb-xa)
    b0 = fx(xa) - m*xa
    linea = b0 + m*xk
    recta = recta + list(linea)

# Marcadores 'o' de xa y xb por tramos
puntox = np.concatenate((aj,bj))
puntoy = fx(puntox)

# Trazado de lineas
plt.plot(xj,recta, label = 'grado 1', color = 'tab:orange')
plt.fill_between(xj,0,recta, color='tab:olive')
plt.plot(xj,fj, label='f(x)', color = 'blue')

# Verticales para dividir los tramos
for i in range(0,len(subtramo),1):
    plt.axvline(subtramo[i], color='tab:gray')
    
# Marcadores de puntos xa y xb por tramos
for j in range(0,len(aj),1):
    plt.axvline(aj[j], color='w')
    plt.axvline(bj[j], color='w')
plt.plot(puntox,puntoy, 'o', color='g')

plt.title('Integral: Cuadratura Gauss')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()

plt.show()

[ Cuadratura de Gauss ] [ Ejercicio ] [Algoritmo/función Python]

Referencia: Tabla 22.1 Chapra p661

Para un integral con intervalo centrado en el origen.

I \cong c_0 f(x_0) + c_1f(x_1) + … + c_{n-1}f(x_{n-1})

Factores usados en las fórmulas de Gauss-Legendre.
Puntos	Factor de ponderación	Argumentos de la función	Error de truncamiento
2	c0 = 1.0000000 c1 = 1.0000000	x0 = – 0.577350269 x1 = 0.577350269	≅ f⁽⁴⁾⁽x )
3	c0 = 0.5555556 c1 = 0.8888889 c2 = 0.5555556	x0 = – 0.774596669 x1 = 0.0 x2 = 0.774596669	≅ f⁽⁶⁾(x )
4	c0 = 0.3478548 c1 = 0.6521452 c2 = 0.6521452 c3 = 0.3478548	x0 = – 0.861136312 x1 = – 0.339981044 x2 = 0.339981044 x3 = 0.861136312	≅f (8)(x )